ТЕМА 15. ПРЯМІ, ЩО ПЕРЕТИНАЮТЬСЯ;
ПЕРПЕНДИКУЛЯРНІ ПРЯМІ. ПАРАЛЕЛЬНІ ПРЯМІ
Варіант 1.
Середній рівень
1. 1) Провести пряму a, яка співпадає з горизонтальною лінією зошита в клітинку. За допомогою транспортира провести пряму b, яка перетинає пряму a під кутом 40º.
2) Провести пряму c, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку A, що не належить прямій c. За допомогою кутника провести пряму a, що проходить через точку A і перпендикулярна до прямої c.
3) Провести пряму m і позначити точку P, що їй не належить. За допомогою кутника провести з точки P перпендикуляр до прямої m. Знайти вимірюванням відстань від точки P до прямої m.
4) Провести пряму d, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку С, що їй не належить. За допомогою кутника провести через точку С пряму c, паралельну прямій d. Знайти відстань між прямими c і d.
2. Накреслити довільний тупокутний трикутник ABC з тупим кутом. Провести перпендикуляр з точки A до прямої BC і перпендикуляр з точки B до прямої AC. Знайти відстань від точки C до прямої AB.
3. Провести пряму a і за допомогою транспортира провести паралельні прямі c і d, які перетинають пряму під кутом 60º. Побудувати спільний перпендикуляр до прямих c і d та знайти відстань між цими прямими.
Достатній рівень
1. 1) Накреслити прямі m і n, що перетинаються під кутом 70º. Утворені нерзгорнуті кути позначити через 1—4 і записати їх градусні міри.
2) Накреслити паралельні прямі a і b, відстань між якими дорівнює 3 см. Побудувати тупокутний трикутник ABC з тупим кутом A, в якого вершини A і C належать прямій a, а вершина B — прямій b. Провести перпендикуляр з вершини A до прямої AB і знайти їх довжини.
2. За допомогою кутника накреслити паралельні прямі a і b і провести паралельні прямі с і d, що перетинають пряму a, під кутом 30º. Знайти вимірність систем, відстань між прямими a і b та с і d.
3. Провести паралельні прямі a і b та пряму пряму c, що перетинає пряму a під кутом 35º. Нерозгорнуті кути, утворені при перетині прямих b і c позначити через 1 — 4 і знайти їх градусні міри.
Високий рівень
1. 1) Провести прямі m і n, що перетинаються так, щоб сума двох утворених гострих кутів дорівнювала 70º.
2) Побудувати тупокутний трикутник ABC з тупим кутом C, в якого вершина B знаходиться від прямої AC на відстані 3 см. Знайти відстані вершини A від прямої BC і вершини C від прямої AB.
2. Провести паралельні прямі a і b. Через точки A і D прямої a провести паралельні прямі c і d, які перетинають пряму a під кутом 50º. Точки перетину прямих c і d з прямою b позначити відповідно через c і d. Записати паралельні сторони утвореного чотирикутника ABCD і знайти без вимірювання його кут.
3. Відсоткове відношення двох нерозгорнутих кутів, утворених при перетині двох прямих дорівнює 50%. Знайти градусну міру гострого кута, утвореного при перетині.
Варіант 2.
Середній рівень
1. 1) Провести пряму m, яка співпадає з горизонтальною лінією зошита в клітинку. За допомогою транспортира провести пряму c, яка перетинає пряму m під кутом 30º.
2) Провести пряму b, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку A, що не належить прямій b. За допомогою кутника провести пряму b, що проходить через точку A і перпендикулярна до прямої b.
3) Провести пряму c і позначити точку K, що їй не належить. За допомогою кутника провести з точки K перпендикуляр до прямої c. Знайти вимірюванням відстань від точки K до прямої c.
4) Провести пряму a, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку B, що їй не належить. За допомогою кутника провести через точку B пряму m, паралельну прямій a. Знайти відстань між прямими m і a.
2. Накреслити довільний тупокутний трикутник ABC з тупим кутом B. Провести перпендикуляр з точки A до прямої BC і перпендикуляр з точки B до прямої AC. Знайти відстань від точки C до прямої AB.
3. Провести пряму a і за допомогою транспортира провести паралельні прямі m і n, які перетинають пряму під кутом 40º. Побудувати спільний перпендикуляр до прямих m і n та знайти відстань між цими прямими.
Достатній рівень
1. 1) Накреслити прямі a і c, що перетинаються під кутом 80º. Утворені нерзгорнуті кути позначити через 1—4 і записати їх градусні міри.
2) Накреслити паралельні прямі m і n, відстань між якими дорівнює 4 см. Побудувати тупокутний трикутник ABC з тупим кутом C, в якого вершини A і C належать прямій a, а вершина B — прямій b. Провести перпендикуляр з вершини C до прямої AB, з вершини A до прямої BC. Знайти їх довжини.
2. За допомогою кутника накреслити паралельні прямі a і c і провести паралельні прямі m і n, що перетинають пряму a, під кутом 40º. Знайти вимірність систем, відстань між прямими a і c та m і n.
3. Провести паралельні прямі a і b та пряму пряму c, що перетинає пряму c під кутом 45º. Нерозгорнуті кути, утворені при перетині прямих b і c позначити через 1 — 4 і знайти їх градусні міри.
Високий рівень
1. 1) Провести прямі m і n, що перетинаються так, щоб сума двох утворених гострих кутів дорівнювала 80º.
2) Побудувати тупокутний трикутник ABC з тупим кутом B, в якого вершина B знаходиться від прямої AC на відстані 2,5 см. Знайти відстані вершини B від прямої AC і вершини A від прямої BC.
2. Провести паралельні прямі a і b. Через точки A і D прямої a провести паралельні прямі c і d, які перетинають пряму a під кутом 70º. Точки перетину прямих c і d з прямою b позначити відповідно через c і d. Записати паралельні сторони утвореного чотирикутника ABCD і знайти без вимірювання його кут.
3. Відсоткове відношення двох нерозгорнутих кутів, утворених при перетині двох прямих дорівнює 200%. Знайти градусну міру тупого кута, утвореного при перетині.
Варіант 3.
Середній рівень
1. 1) Провести пряму b, яка співпадає з горизонтальною лінією зошита в клітинку. За допомогою транспортира провести пряму m, яка перетинає пряму b під кутом 50º.
2) Провести пряму c, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку B, що не належить прямій c. За допомогою кутника провести пряму c, що проходить через точку B і перпендикулярна до прямої c.
3) Провести пряму m і позначити точку K, що їй не належить. За допомогою кутника провести з точки K перпендикуляр до прямої m. Знайти вимірюванням відстань від точки K до прямої m.
4) Провести пряму a, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку D, що їй не належить. За допомогою кутника провести через точку D пряму c, паралельну прямій a. Знайти відстань між прямими c і a.
2. Накреслити довільний тупокутний трикутник ABC з тупим кутом C. Провести перпендикуляр з точки A до прямої BC і перпендикуляр з точки B до прямої AC. Знайти відстань від точки C до прямої AB.
3. Провести пряму c і за допомогою транспортира провести паралельні прямі m і n, які перетинають пряму під кутом 65º. Побудувати спільний перпендикуляр до прямих m і n та знайти відстань між цими прямими.
Достатній рівень
1. 1) Накреслити прямі a і b, що перетинаються під кутом 40º. Утворені нерзгорнуті кути позначити через 1—4 і записати їх градусні міри.
2) Накреслити паралельні прямі m і p, відстань між якими дорівнює 2,5 см. Побудувати тупокутний трикутник ABC з тупим кутом B, в якого вершини A і C належать прямій a, а вершина B — прямій b. Провести перпендикуляр з вершини B до прямої AC і з вершини C до прямої AB. Знайти їх довжини.
2. За допомогою кутника накреслити паралельні прямі m і n і провести паралельні прямі с і d, що перетинають пряму c, під кутом 25º. Знайти вимірність систем, відстань між прямими m і n та с і d.
3. Провести паралельні прямі a і b та пряму p, що перетинає пряму a під кутом 40º. Нерозгорнуті кути, утворені при перетині прямих b і c позначити через 1 — 4 і знайти їх градусні міри.
Високий рівень
1. 1) Провести прямі a і b, що перетинаються так, щоб сума двох утворених гострих кутів дорівнювала 150º.
2) Побудувати тупокутний трикутник MNK з тупим кутом N, в якого вершина M знаходиться від прямої NK на відстані 3,5 см. Знайти відстані вершини N від прямої MK і вершини K від прямої MN.
2. Провести паралельні прямі a і b. Через точки A і D прямої a провести паралельні прямі c і d, які перетинають пряму a під кутом 65º. Точки перетину прямих c і d з прямою b позначити відповідно через c і d. Записати паралельні сторони утвореного чотирикутника ABCD і знайти без вимірювання його кут.
3. Відсоткове відношення двох нерозгорнутих кутів, утворених при перетині двох прямих дорівнює 20%. Знайти градусну міру гострого кута, утвореного при перетині.
Варіант 4.
Середній рівень
1. 1) Провести пряму a, яка співпадає з горизонтальною лінією зошита в клітинку. За допомогою транспортира провести пряму m, яка перетинає пряму c під кутом 60º.
2) Провести пряму m, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку P, що не належить прямій m. За допомогою кутника провести пряму m, що проходить через точку P і перпендикулярна до прямої m.
3) Провести пряму b і позначити точку D, що їй не належить. За допомогою кутника провести з точки D перпендикуляр до прямої b. Знайти вимірюванням відстань від точки D до прямої b.
4) Провести пряму c, яка перетинає горизонтальну лінію зошита під деяким гострим кутом, і позначити точку K, що їй не належить. За допомогою кутника провести через точку K пряму c, паралельну прямій c. Знайти відстань між прямими b і c.
2. Накреслити довільний тупокутний трикутник MOK з тупим кутом M. Провести перпендикуляр з точки M до прямої OK і перпендикуляр з точки O до прямої MK. Знайти відстань від точки K до прямої MK.
3. Провести пряму a і за допомогою транспортира провести паралельні прямі c і d, які перетинають пряму під кутом 35º. Побудувати спільний перпендикуляр до прямих c і d та знайти відстань між цими прямими.
Достатній рівень
1. 1) Накреслити прямі m і n, що перетинаються під кутом 60º. Утворені нерзгорнуті кути позначити через 1—4 і записати їх градусні міри.
2) Накреслити паралельні прямі b і c, відстань між якими дорівнює 3,5 см. Побудувати тупокутний трикутник BCD з тупим кутом C, в якого вершини C і D лежать на прямій с, а вершина B — прямій b. Провести перпендикуляр з вершини С до прямої BD і з вершини B до прямої CD. Знайти їх довжини.
2. За допомогою кутника накреслити паралельні прямі m і n і провести паралельні прямі с і d, що перетинають пряму c, під кутом 70º. Знайти вимірність систем, відстань між прямими m і n та с і d.
3. Провести паралельні прямі m і n та пряму a, що перетинає пряму a під кутом 55º. Нерозгорнуті кути, утворені при перетині прямих b і c позначити через 1 — 4 і знайти їх градусні міри.
Високий рівень
1. 1) Провести прямі a і c, що перетинаються так, щоб сума двох утворених гострих кутів дорівнювала 120º.
2) Побудувати тупокутний трикутник MNK з тупим кутом M, в якого вершина M знаходиться від прямої NK на відстані 4 см. Знайти відстані вершини M від прямої NK і вершини N від прямої MK.
2. Провести паралельні прямі a і b. Через точки A і D прямої a провести паралельні прямі c і d, які перетинають пряму a під кутом 45º. Точки перетину прямих c і d з прямою b позначити відповідно через c і d. Записати паралельні сторони утвореного чотирикутника ABCD і знайти без вимірювання його кут.
3. Відсоткове відношення двох нерозгорнутих кутів, утворених при перетині двох прямих дорівнює 500%. Знайти градусну міру гострого кута, утвореного при перетині.
ТЕМА 16. ПАРАЛЕЛОГРАМИ: ПЕРИМЕТР, ПЛОЩА
Варіант 1.
Середній рівень
1. Знайти периметр і площу:
1) паралелограма, в якого сторони дорівнюють 5 см і 12 см, а висота, що проведена до сторони 12 см, дорівнює 4 см.
2) прямокутника зі сторонами 7 см і 3 см;
3) ромба зі стороною 5 см і висотою 4 см;
4) квадрата зі стороною 5 дм.
2. Одна із сторін паралелограма дорівнює 5 см. Знайти висоту паралелограма, проведену до цієї сторони, якщо його площа 15 см2.
3. Провести паралельні прямі a і b, відстань між якими дорівнює 4 см. Побудувати паралелограм ABCD, в якого вершини A і D належать прямій a, вершини B і С — прямій b, і AD = 6 см, AB = 5 см. Провести висоту паралелограма х вершини B до сторони AD, записати її довжину і обчислити периметр та площу паралелограма.
Достатній рівень
1. 1) Периметр паралелограма дорівнює 40 см, а одна із сторін 8 см. Знайти сторону паралелограма, сусідню з даною.
2) Побудувати паралелограм ABCD, в якого сторона AD дорівнює 4 см, висота BK, що проведена до неї, дорівнює 3 см, а сторона AB — 6 см. Провести ивсоту BM до сторони CD. Обчислити площу паралелограма і висоту BM.
2. Знайти сторони паралелограма, якщо вони відносяться, як 2: 3, а периметр паралелограма дорівнює 20 см.
3. Висоти паралелограма дорівнюють 3 см і 4 см. Знайти більшу сторону паралелограма, якщо менша сторона дорівнює 6 см.
Високий рівень
1. 1) Виконати необхідні обчислення і побудувати парлелограм, у якого дві сторони дорівнюють 4 см і 5 см, а площа паралелограма 15 см2.
2) Висоти паралелограма дорівнюють 8 дм і 6 дм, а більша сторона 12 дм. Обчислити периметр паралелограма.
2. Знайти площу паралелограма, в якого сторони дорівнюють 8 см і 12 см, а сума висоти дорівнює 10 см.
3. Відсоткове відношення сторони a паралелограма до сторони b дорівнює 80%. Знайти відсоткове відношення висоти, проведеної до сторони a, і висоти, проведеної до сторони b.
Варіант 2.
Середній рівень
1. Знайти периметр і площу:
1) паралелограма, в якого сторони дорівнюють 20 см і 6 см, а висота, що проведена до сторони 6 см, дорівнює 7 см.
2) прямокутника зі сторонами 5 см і 12 см;
3) ромба зі стороною 7 см і висотою 5 см;
4) квадрата зі стороною9 дм.
2. Одна із сторін паралелограма дорівнює 7 см. Знайти висоту паралелограма, проведену до цієї сторони, якщо його площа 28 см2.
3. Провести паралельні прямі a і b, відстань між якими дорівнює 3 см. Побудувати паралелограм ABCD, в якого вершини A і D належать прямій a, вершини B і С — прямій b, і AD = 7 см, AB = 4 см. Провести висоту паралелограма х вершини B до сторони AD, записати її довжину і обчислити периметр та площу паралелограма.
Достатній рівень
1. 1) Периметр паралелограма дорівнює 30 см, а одна із сторін 10 см. Знайти сторону паралелограма, сусідню з даною.
2) Побудувати паралелограм ABCD, в якого сторона AD дорівнює 3 см, висота BK, що проведена до неї, дорівнює 4 см, а сторона AB — 6 см. Провести ивсоту BM до сторони CD. Обчислити площу паралелограма і висоту BM.
2. Знайти сторони паралелограма, якщо вони відносяться, як 2: 3, а периметр паралелограма дорівнює 42 см.
3. Висоти паралелограма дорівнюють 6 см і 4 см. Знайти меншу сторону паралелограма, якщо більша сторона дорівнює 12 см.
Високий рівень
1. 1) Виконати необхідні обчислення і побудувати ромб, у якого сторона дорівнює 5 см, а площа дорівнює 20 см2.
2) Висоти паралелограма дорівнюють 6 дм і 8 дм, а менша сторона 12 дм. Обчислити периметр паралелограма.
2. Знайти площу паралелограма, в якого сторони дорівнюють 30 см і 24 см, а сума висоти дорівнює 18 см.
3. Відсоткове відношення сторони a паралелограма до сторони b дорівнює 20%. Знайти відсоткове відношення висоти, проведеної до сторони a, і висоти, проведеної до сторони b.
Варіант 3.
Середній рівень
1. Знайти периметр і площу:
1) паралелограма, в якого сторони дорівнюють 8 см і 5 см, а висота, що проведена до сторони 5 см, дорівнює 6 см.
2) прямокутника зі сторонами 6 см і 4 см;
3) ромба зі стороною 10 см і висотою 7 см;
4) квадрата зі стороною 8 дм.
2. Одна із сторін паралелограма дорівнює 4 см. Знайти висоту паралелограма, проведену до цієї сторони, якщо його площа 20 см2.
3. Провести паралельні прямі a і b, відстань між якими дорівнює 2,5 см. Побудувати паралелограм ABCD, в якого вершини A і D належать прямій a, вершини B і С — прямій b, і AD = 6 см, AB = 4 см. Провести висоту паралелограма х вершини B до сторони AD, записати її довжину і обчислити периметр та площу паралелограма.
Достатній рівень
1. 1) Периметр паралелограма дорівнює 34 см, а одна із сторін 6 см. Знайти сторону паралелограма, сусідню з даною.
2) Побудувати паралелограм ABCD, в якого сторона AD дорівнює 4 см, висота BK, що проведена до неї, дорівнює 1,5 см, а сторона AB — 3 см. Провести ивсоту BM до сторони CD. Обчислити площу паралелограма і висоту BM.
2. Знайти сторони паралелограма, якщо вони відносяться, як 2: 5, а периметр паралелограма дорівнює 28 см.
3. Висоти паралелограма дорівнюють 3 см і 4 см. Знайти більшу сторону паралелограма, якщо менша сторона дорівнює 9 см.
Високий рівень
1. 1) Виконати необхідні обчислення і побудувати парлелограм, у якого дві сторони дорівнюють 3 см і 4 см, а площа паралелограма 10 см2.
2) Висоти паралелограма дорівнюють 8 см і 5 см, а більша сторона 10 см. Обчислити периметр паралелограма.
2. Знайти площу паралелограма, в якого сторони дорівнюють 16 см і 12 см, а сума висоти дорівнює 14 см.
3. Відсоткове відношення сторони a паралелограма до сторони b дорівнює 25%. Знайти відсоткове відношення висоти, проведеної до сторони a, і висоти, проведеної до сторони b.
Варіант 4.
Середній рівень
1. Знайти периметр і площу:
1) паралелограма, в якого сторони дорівнюють 6 см і 10 см, а висота, що проведена до сторони 10 см, дорівнює 5 см.
2) прямокутника зі сторонами 4 см і 3 см;
3) ромба зі стороною 9 см і висотою 6 см;
4) квадрата зі стороною 7 дм.
2. Одна із сторін паралелограма дорівнює 9 см. Знайти висоту паралелограма, проведену до цієї сторони, якщо його площа 54 см2.
3. Провести паралельні прямі a і b, відстань між якими дорівнює 3,5 см. Побудувати паралелограм ABCD, в якого вершини A і D належать прямій a, вершини B і С — прямій b, і AD = 4 см, AB = 5 см. Провести висоту паралелограма х вершини B до сторони AD, записати її довжину і обчислити периметр та площу паралелограма.
Достатній рівень
1. 1) Периметр паралелограма дорівнює 54 см, а одна із сторін 15 см. Знайти сторону паралелограма, сусідню з даною.
2) Побудувати паралелограм ABCD, в якого сторона AD дорівнює 4 см, висота BK, що проведена до неї, дорівнює 2,5 см, а сторона AB — 5 см. Провести ивсоту BM до сторони CD. Обчислити площу паралелограма і висоту BM.
2. Знайти сторони паралелограма, якщо вони відносяться, як 3: 5, а периметр паралелограма дорівнює 48 см.
3. Висоти паралелограма дорівнюють 4 см і 5 см. Знайти меншу сторону паралелограма, якщо більша сторона дорівнює 15 см.
Високий рівень
1. 1) Виконати необхідні обчислення і побудувати ромб, у якого сторона дорівнює 4 см, а площа дорівнює 12 см2.
2) Висоти паралелограма дорівнюють 9 см і 5 см, а більша сторона 10 см. Обчислити периметр паралелограма.
2. Знайти площу паралелограма, в якого сторони дорівнюють 24 см і 18 см, а сума висоти дорівнює 14 см.
3. Відсоткове відношення сторони a паралелограма до сторони b дорівнює 50%. Знайти відсоткове відношення висоти, проведеної до сторони a, і висоти, проведеної до сторони b.
ТЕМА 17. ТРИКУТНИКИ: ПЕМЕТР, ПЛОЩА
Варіант 1.
Середній рівень
1. Знайти:
1) периметр рівностороннього трикутника зі стороною 5 см.
2) периметр рівнобедреного трикутника зосновою 5 см і бічною стороню 4 см;
3) площу трикутника, в якого одна із сторін дорівнює 10 см, а висота, що проведена до неї, 4 см;
4) площу прямокутного трикутника, в якого сторони, що утворюють прямий кут, дорівнюють 2 см і 5 см.
2. Побудувати прямокутний трикутник, в якого сторони, що утворюють прямий кут дорівнюють 3 см і 4 см, і обчислити його площу.
3. Накреслити паралельні прямі a і b, відстань між якими дорівнює 4 см. На прямій a відкласти відрізок AC = 5 см, а на прямій b позначити довільну точку B і сполучити її відрізками з точками A і C. Обчислити площу трикутника ABC. Чи залежить площа трикутника від положення точки B на прямій b?
Достатній рівень
1. Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 7 см, висота, що проведена до неї, 3 см, а сторона дорівнює 5 см.
1) Обчислити площу трикутника.
2) Виміряти сторону BC і знайти периметр трикутника ABC.
2. Периметр рівнобедреного трикутника дорівнює 22 см, а його основа 10 см. Знайти довжину бічної сторони трикутника.
3. Одна із сторін трикутника дорівнює 6 см, а його площа дорівнює 30 см2.
Вказівка. Використати формулу a × ha = 2 S, де а — сторона трикутника, ha — висота, що проведена до неї, 2 S — подвійна площа трикутника.
Високий рівень
1. 1) Знайти основу і бічну сторону рівнобедреного трикутника, якщо вони відносяться, як 2: 3, а периметр трикутника дорівнює 40 см.
2) Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 3 см, висота, що проведена до неї, 4 см, а сторона AB дорівнює 6 см. Обчислити площу трикутника ABC і висоту, що проведена до сторони AC.
2. У трикутнику сторона a дорівнює 6 см, а сторона b дорівнює 8 см. Знайти 
відношення висот, проведених до цих сторін.
3. Знайти площу трикутника, в якого дві сторони дорівнюють 10 см і 16 см, а сума висот, проведених до цих сторін, дорівнюєх 13 см.
Варіант 2.
Середній рівень
1. Знайти:
1) периметр рівностороннього трикутника зі стороною 4 см.
2) периметр рівнобедреного трикутника зосновою 6 см і бічною стороню 5 см;
3) площу трикутника, в якого одна із сторін дорівнює 8 см, а висота, що проведена до неї, 4 см;
4) площу прямокутного трикутника, в якого сторони, що утворюють прямий кут, дорівнюють 3 см і 10 см.
2. Побудувати прямокутний трикутник, в якого сторони, що утворюють прямий кут дорівнюють 2 см і 3 см, і обчислити його площу.
3. Накреслити паралельні прямі a і b, відстань між якими дорівнює 3 см. На прямій a відкласти відрізок AC = 4 см, а на прямій b позначити довільну точку B і сполучити її відрізками з точками A і C. Обчислити площу трикутника ABC. Чи залежить площа трикутника від положення точки B на прямій b?
Достатній рівень
1. Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 3 см, висота, що проведена до неї, 4 см, AB = 5 см.
1) Обчислити площу трикутника.
2) Виміряти сторону BC і знайти периметр трикутника ABC.
2. Периметр рівнобедреного трикутника дорівнює 18 см, а його основа 8 см. Знайти довжину бічної сторони трикутника.
3. Одна із сторін трикутника дорівнює 7 см, а його площа дорівнює 35 см2.
Вказівка. Використати формулу a × ha = 2 S, де а — сторона трикутника, ha — висота, що проведена до неї, 2 S — подвійна площа трикутника.
Високий рівень
1. 1) Знайти основу і бічну сторону рівнобедреного трикутника, якщо вони відносяться, як 4: 3, а периметр трикутника дорівнює 40 см.
2) Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 2,5 см, висота, що проведена до неї, 4 см, а сторона AB дорівнює 5 см. Обчислити площу трикутника ABC і висоту, що проведена до сторони AC.
2. У трикутнику сторона a дорівнює 12 см, а сторона b дорівнює 15 см. Знайти відношення висот, проведених до цих сторін.
3. Знайти площу трикутника, в якого дві сторони дорівнюють 10 см і 18 см, а сума висот, проведених до цих сторін, дорівнюєх 14 см.
Варіант 3.
Середній рівень
1. Знайти:
1) периметр рівностороннього трикутника зі стороною 3 см.
2) периметр рівнобедреного трикутника зосновою 8 см і бічною стороню 6 см;
3) площу трикутника, в якого одна із сторін дорівнює 9 см, а висота, що проведена до неї, 6 см;
4) площу прямокутного трикутника, в якого сторони, що утворюють прямий кут, дорівнюють 4 см і 8 см.
2. Побудувати прямокутний трикутник, в якого сторони, що утворюють прямий кут дорівнюють 2 см і 5 см, і обчислити його площу.
3. Накреслити паралельні прямі a і b, відстань між якими дорівнює 2,5 см. На прямій a відкласти відрізок AC = 4 см, а на прямій b позначити довільну точку B і сполучити її відрізками з точками A і C. Обчислити площу трикутника ABC. Чи залежить площа трикутника від положення точки B на прямій b?
Достатній рівень
1. Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 4 см, висота, що проведена до неї, 2,5 см, а AB дорівнює см.
1) Обчислити площу трикутника.
2) Виміряти сторону BC і знайти периметр трикутника ABC.
2. Периметр рівнобедреного трикутника дорівнює 25 см, а його бічна сторона — 7 см. Знайти основу трикутника.
3. Площа трикутника дорівнює 14 см2. Одна з його висот дорівнює 4 см. Знайти довжину сторони, до якої проведена ця висота.
Високий рівень
1. 1) Знайти основу і бічну сторону рівнобедреного трикутника, якщо вони відносяться, як 5: 3, а периметр трикутника дорівнює 55 см.
2) Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 2,5 см, висота, що проведена до неї, 4 см, а сторона AB дорівнює 5 см. Обчислити площу трикутника ABC і висоту, що проведена до сторони AC.
2. У трикутника ha — висота, що проведена до сторони a, дорівнює 8 см, а hb — висота, що проведена до сторони b, дорівнює 6 см. Знайти відношення висот, проведених до цих сторін 
.
3. Знайти площу трикутника, в якого дві висоти дорівнюють 8 см і 6 см, а сума сторін, до яких проведені висоти дорівнює 28 см.
Варіант 4.
Середній рівень
1. Знайти:
1) периметр рівностороннього трикутника зі стороною 6 дм.
2) периметр рівнобедреного трикутника зосновою 7 см і бічною сторонює 4 см;
3) площу трикутника, в якого одна із сторін дорівнює 6 см, а висота, що проведена до неї, 5 см;
4) площу прямокутного трикутника, в якого сторони, що утворюють прямий кут, дорівнюють 12 см і 10 см.
2. Побудувати прямокутний трикутник, в якого сторони, що утворюють прямий кут дорівнюють 3 см і 5 см, і обчислити його площу.
3. Накреслити паралельні прямі a і b, відстань між якими дорівнює 3,5 см. На прямій a відкласти відрізок AC = 2 см, а на прямій b позначити довільну точку B і сполучити її відрізками з точками A і C. Обчислити площу трикутника ABC. Чи залежить площа трикутника від положення точки B на прямій b?
Достатній рівень
1. Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 5 см, висота, що проведена до неї, 3,5 см, AB = 4 см.
1) Обчислити площу трикутника.
2) Виміряти сторону BC і знайти периметр трикутника ABC.
2. Периметр рівнобедреного трикутника дорівнює 21 см, а його основа 6 см. Знайти довжину бічної сторони трикутника.
3. Площа трикутника дорівнює 40 см2. Одна з його висот дорівнює 8 см. Знайти довжину сторони, до якої проведена ця висота.
Високий рівень
1. 1) Знайти основу і бічну сторону рівнобедреного трикутника, якщо вони відносяться, як 2: 5, а периметр трикутника дорівнює 36 см.
2) Побудувати тупокутний трикутник ABC з тупим кутом A, в якого сторона AC дорівнює 4 см, висота, що проведена до неї, 3,5 см, а сторона AB дорівнює 7 см. Обчислити площу трикутника ABC і висоту, що проведена до сторони AC.
2. У трикутнику сторона a дорівнює 16 см, а сторона b дорівнює 12 см. Знайти відношення висот, проведених до цих сторін.
3. Знайти площу трикутника, в якого дві сторони дорівнюють 18 см і 10 см, а сума висот, проведених до цих сторін, дорівнюєх 56 см.
ТЕМА 18. ДОВЖИНА КОЛА. ПЛОЩА КРУГА
Варіант 1.
Середній рівень
1. Знайти:
1) діаметр кола, якщо його радіус дорівнює 4 см;
2) радіус кола, якщо його діаметр дорівнює 12 см;
3) довжину кола радіуса 5 см (p» 3);
4) площу круга радіуса 6 дм (p» 3).
2. Обчислити довжину кола і площу круга радіуса 10 см (p» 3,14).
3. Обчислити довжину кола і площу круга, діаметр якого дорівнюєх 6 см.
Достатній рівень
1. 1) Довжина кола дорівнює 62,8 см. Обчислити його радіус.
2) Радіус першого круга дорівнює 10 см, а другого — 5 см. Знайти відношення площі першого круга до площі другого круга.
2. Обчислити площу круга, довжина кола якого дорівнює 93 м (p» 3,1).
3. Який шлях пройде за 15 хв кінець хвилинної стрілки годинника, довжина якої 4 м.
Високий рівень
1. 1) Треба зафарбувати чверть круга радіуса 4 м. Скільки потрібно для цього фарби, якщо на кожний квадратний метр витрачається 100 г фарби.
2) Кінець хвилинної стрілки годинника за 20 хв проходить шлях, який дорівнює 6,28 м. Знайти довжину стрілки.
2. Довжину кола збільшили з 6,28 см до 12,56 см.
На скільки збільшився радіус кола?
3. Визначити площу фігури,
зображеної на рисунку.
Рис. 1
Варіант 2.
Середній рівень
1. Знайти:
1) діаметр кола, якщо його радіус дорівнює 10 см;
2) радіус кола, якщо його діаметр дорівнює 18 см;
3) довжину кола радіуса 4 см (p» 3);
4) площу круга радіуса 2 дм (p» 3).
2. Обчислити довжину кола і площу круга радіуса 1 см (p» 3,14).
3. Обчислити довжину кола і площу круга, діаметр якого дорівнюєх 10 см.
Достатній рівень
1. 1) Довжина кола дорівнює 12,56 см. Обчислити його радіус.
2) Радіус першого круга дорівнює 4 см, а другого — 1 см. Знайти відношення площі першого круга до площі другого круга.
2. Обчислити площу круга, довжина кола якого дорівнює 6,2 дм (p» 3,1).
3. Який шлях пройде за 20 хв кінець хвилинної стрілки годинника, довжина якої 4 м.
Високий рівень
1. 1) Треба зафарбувати півкруга радіуса 2 м. Скільки потрібно для цього фарби, якщо на кожний квадратний метр витрачається 100 г фарби.
2) Кінець хвилинної стрілки годинника за 15 хв проходить шлях, який дорівнює 6,28 м. Знайти довжину стрілки.
2. Довжину кола збільшили з 12,56 см до 25,12 см.
На скільки збільшився радіус кола?
3. Визначити площу фігури,
зображеної на рисунку.
Рис. 2
Варіант 3.
Середній рівень
1. Знайти:
1) діаметр кола, якщо його радіус дорівнює 6 см;
2) радіус кола, якщо його діаметр дорівнює 24 см;
3) довжину кола радіуса 12 см (p» 3);
4) площу круга радіуса 5 дм (p» 3).
2. Обчислити довжину кола і площу круга радіуса 5 см (p» 3,14).
3. Обчислити довжину кола і площу круга, діаметр якого дорівнюєх 4 дм.
Достатній рівень
1. 1) Довжина кола дорівнює 31,4 см. Обчислити його радіус.
2) Радіус першого круга дорівнює 3 дм, а другого — 1 дм. Знайти відношення площі першого круга до площі другого круга.
2. Обчислити площу круга, довжина кола якого дорівнює 62 см (p» 3,1).
3. Який шлях пройде за 30 хв кінець хвилинної стрілки годинника, довжина якої 2 м.
Високий рівень
1. 1) Треба зафарбувати чверть круга радіуса 2 м. Скільки потрібно для цього фарби, якщо на кожний квадратний метр витрачається 100 г фарби.
2) Кінець хвилинної стрілки годинника за 10 хв проходить шлях, який дорівнює 3,14 м. Знайти довжину стрілки.
2. Довжину кола збільшили з 6,28 см до 18,84 см.
На скільки збільшився радіус кола?
3. Визначити площу фігури,
зображеної на рисунку.
Рис. 3
Варіант 4.
Середній рівень
1. Знайти:
1) діаметр кола, якщо його радіус дорівнює 7 см;
2) радіус кола, якщо його діаметр дорівнює 26 дм;
3) довжину кола радіуса 9 см (p» 3);
4) площу круга радіуса 3 дм (p» 3).
2. Обчислити довжину кола і площу круга радіуса 2 дм (p» 3,14).
3. Обчислити довжину кола і площу круга, діаметр якого дорівнюєх 8 см.
Достатній рівень
1. 1) Довжина кола дорівнює 6,28 см. Обчислити його радіус.
2) Радіус першого круга дорівнює 4 см, а другого — 2 см. Знайти відношення площі першого круга до площі другого круга.
2. Обчислити площу круга, довжина кола якого дорівнює 31 см (p» 3,1).
3. Який шлях пройде за 10 хв кінець хвилинної стрілки годинника, довжина якої 6 дм.
Високий рівень
1. 1) Треба зафарбувати півкруга радіуса 10 м. Скільки потрібно для цього фарби, якщо на кожний квадратний метр витрачається 100 г фарби.
2) Кінець хвилинної стрілки годинника за 30 хв проходить шлях, який дорівнює 6,28 м. Знайти довжину стрілки.
2. Довжину кола збільшили з 6,28 см до 25,12 см.
На скільки збільшився радіус кола?
3. Визначити площу фігури,
зображеної на рисунку.
Рис. 3
ТЕМА 19. ПРЯМА ПРИЗМА
Варіант 1.
Середній рівень
1. Знайти:
1) об’єм прямої призми, висота якої дорівнює 12 см, а площа основи дорівнює 30 см2;
2) площу бічної поверхні прямої призми, висота якої дорівнює 8 см, а периметр основи дорівнює 20 см;
3) площу повної поверхні прямої призми, площа основи якої дорівнює 10 см2, а площа бічної поверхні — 50 см2.
2. 1) Основою призми є трикутник, одна із сторін якого дорівнює 16 см, а висота, що проведена до неї дорівнює 10 см. Знайти об’єм призми, якщо її висота дорівнює 20 см.
2) Основою прямої призми є рівносторонній трикутник із стороною 6 см. Знайти площу бічної поверхні призми, якщо висота призми дорівнює 20 см.
3. Основою прямої призми є прямокутник із сторонами 4 см і 6 см. Висота призми дорівнює 5 см. Знайти: а) площу основи і об’єм призми; б) периметр основи і площу бічної поверхні призми; в) площу повної поверхні призми.
Достатній рівень
1. Основою прямої призми є паралелограм, сторони якого дорівнюють 5 см і 12 см. Висота паралелограма, що проведена до більшої його сторони, дорівнює 40 см. Висота призми дорівнює 10 см. Знайти:
1) об’єм призми; 2) площу бічної і повної поверхні призми.
2. Основою прямої призми є шестикутник з рівними сторонами, кожна з яких дорівнює 5 см.
3. Площа кожної бічної грані п’ятикутної призми дорівнює 30 см2. Знайти площу повної поверхні призми, якщо площа основи призми у 3 рази менша від площі іншої поверхні..
Високий рівень
1. Основою прямої призми є паралелограм зі сторонами 8 см і 6 см. Висота паралелограма, що проведена до більшої сторони, дорівнює 5 см. Обчислити площу повної поверхні призми, якщо її об’єм дорівнює 180 см3 = 480см3.
2. За даною розгорткою призми
(прямокутного паралелепіпеда)
обчислити площу повної поверхні призми.
3. Скільки у 40-кутної призми:
а) граней; б) бічних граней; в) ребер;
Г) бічних ребер; д) вершин?Рис.
Варіант 2.
Середній рівень
1. Знайти:
1) об’єм прямої призми, висота якої дорівнює 14 см, а площа основи дорівнює 20 см2;
2) площу бічної поверхні прямої призми, висота якої дорівнює 7 см, а периметр основи дорівнює 30 см;
3) площу повної поверхні прямої призми, площа основи якої дорівнює 20 дм2, а площа бічної поверхні — 80 дм2.
2. 1) Основою призми є паралелограм, одна із сторін якого дорівнює 10 см, а висота, що проведена до неї дорівнює 4 см. Знайти об’єм призми, якщо її висота дорівнює 8 см.
2) Основою прямої призми є рівнобедрений трикутник з основою 10 см і бічною стороню 8 см. Знайти площу бічної поверхні призми, якщо висота призми дорівнює 12 см.
3. Основою прямої призми є прямокутник із сторонами 5 см і 7 см. Висота призми дорівнює 10 см. Знайти: а) площу основи і об’єм призми; б) периметр основи і площу бічної поверхні призми; в) площу повної поверхні призми.
Достатній рівень
1. Основою прямої призми є прямокутний трикутник, у якого дві сторони, що утворюють прямий кут, дорівнюють 3 см і 4 см, а третя сторона дорівнює 5 см. Висотапризми дорівнює 12 см. Знайти:
1) об’єм призми; 2) площу бічної і повної поверхні призми.
2. Основою прямої призми є п’ятикутник, у якого кожна сторона дорівнює 4 см. Площа бічної поверхні призми дорівнює 240 см2. Знайти висоту призми.
3. Площа кожної бічної грані шестикутної призми дорівнює 40 см2. Знайти площу повної поверхні призми, якщо площа основи призми у 5 разів менша від площі бічної поверхні.
Високий рівень
1. Основою прямої призми є паралелограм зі сторонами 12 см і 16 см. Висота паралелограма, проведена до меншої сторони, дорівнює 10 см. Обчислити об’єм призми, якщо площа її бічної поверхні дорівнює 280 см3.
2. За даною розгорткою прямої трикутної
призми обчислити площу
повної поверхні призми.
3. Скільки у 12-кутної призми:
а) граней; б) бічних граней; в) ребер;
Г) бічних ребер; д) вершин?Рис.
Варіант 3.
Середній рівень
1. Знайти:
1) об’єм прямої призми, висота якої дорівнює 11 см, а площа основи дорівнює 40 см2;
2) площу бічної поверхні прямої призми, висота якої дорівнює 8 см, а периметр основи дорівнює 11 см;
3) площу повної поверхні прямої призми, площа основи якої дорівнює 30 см2, а площа бічної поверхні — 60 см2.
2. 1) Основою призми є паралелограм, одна із сторін якого дорівнює 8 см, а висота, що проведена до неї дорівнює 6 см. Знайти об’єм призми, якщо її висота дорівнює 20 см.
2) Основою прямої призми є трикутник із сторонами 8 см, 7 см і 5 см. Знайти площу бічної поверхні призми, якщо висота призми дорівнює 30 см.
3. Основою прямої призми є прямокутник із сторонами 3 см і 7 см. Висота призми дорівнює 15 см. Знайти: а) площу основи і об’єм призми; б) периметр основи і площу бічної поверхні призми; в) площу повної поверхні призми.
Достатній рівень
1. Основою прямої призми є паралелограм, сторони якого дорівнюють 6 см і 4 см. Висота паралелограма, яка проведена до меншої сторони, дорівнює 5 см. Висота призми дорівнює 15 см. Знайти:
1) об’єм призми; 2) площу бічної і повної поверхні призми.
2. Основою прямої призми є рівносторонній трикутник із стороною 6 см. Площа бічної поверхні призми дорівнює 360 см2. Знайти висоту призми.
3. Площа кожної бічної грані восьмикутної призми дорівнює 30 см2. Знайти площу повної поверхні призми, якщо площа основи призми у 4 рази менша від площі бічної поверхні призми.
Високий рівень
1. Основою прямої призми є паралелограм зі сторонами 5 см і 6 см. Висота паралелограма, що проведена до більшої сторони, дорівнює 4 см. Обчислити площу повної поверхні призми, якщо її об’єм дорівнює 240см3.
2. За даною розгорткою призми
(прямокутного паралелепіпеда)
обчислити площу повної поверхні призми.
3. Скільки у 16-кутної призми:
а) граней; б) бічних граней; в) ребер;
Г) бічних ребер; д) вершин?Рис.
Варіант 4.
Середній рівень
1. Знайти:
1) об’єм прямої призми, висота якої дорівнює 8 см, а площа основи дорівнює 25 см2;
2) площу бічної поверхні прямої призми, висота якої дорівнює 6 см, а периметр основи дорівнює 15 см;
3) площу повної поверхні прямої призми, площа основи якої дорівнює 40 дм2, а площа бічної поверхні — 120 дм2.
2. 1) Основою призми є прямокутний трикутник, у якого сторони, що утворюють прямий кут, дорівнюють 12 см і 6 см. Знайти об’єм призми, якщо її висота дорівнює 10 см.
2) Основою прямої призми є паралелограм із сторонами 8 см і 12 см. Знайти площу бічної поверхні призми, якщо висота призми дорівнює 20 см.
3. Основою прямої призми є прямокутник із сторонами 4 см і 12 см. Висота призми дорівнює 10 см. Знайти: а) площу основи і об’єм призми; б) периметр основи і площу бічної поверхні призми; в) площу повної поверхні призми.
Достатній рівень
1. Основою прямої призми є паралелограм, в якого всі сторони рівні і дорівнюють 5 см, а кожна з висот дорівнює 4 см. Висота призми дорівнює 20 см. Знайти:
1) об’єм призми; 2) площу бічної і повної поверхні призми.
2. Основою прямої призми є восьиикутник, у якого всі сторони рівні, і дорівнюють 4 см. Площа бічної поверхні призми дорівнює 640 см2. Знайти висоту призми.
3. Площа кожної бічної грані десятикутної призми дорівнює 20 см2. Знайти площу повної поверхні призми, якщо площа основи призми у 5 разів менша від площі бічної поверхні призми.
Високий рівень
1. Основою прямої призми є паралелограм зі сторонами 20 см і 15 см. Висота паралелограма, проведена до меншої сторони, дорівнює 16 см. Обчислити об’єм призми, якщо площа її бічної поверхні дорівнює 360 см3.
2. За даною розгорткою прямої трикутної
призми обчислити її об’єм.
3. Скільки у 10-кутної призми:
а) граней; б) бічних граней; в) ребер;
Г) бічних ребер; д) вершин?Рис.
ТЕМА 20. ЦИЛІНДР
Варіант 1.
Середній рівень
1. Знайти:
1) площу повної поверхні циліндра, якщо площа його основи дорівнює 16 см2, а площі бічної поверхні — 80 см2;
2) об’єм циліндра, в якого площа основи дорівнює 3,14 дм2, а висота дорівнює 10 дм;
3) площу бічної поверхні циліндра, у якого радіус основи дорівнює 3 см, а висота — 10 см (p» 3).
2. Обчислити об’єм циліндра, в якого радіус основи дорівнює 2 см, а висота — 6 см.
3. Обчислити площу повної поверхні циліндра, в якого радіус основи дорівнює 6 см, а висота — 20 см.
Достатній рівень
1. Обчислити площу повної поверхні і об’єм циліндра, у якого діаметр основи і висота дорівнюють 8 см.
2. Знайти площу основи циліндра, якщо його висота дорівнює 25 см, а площа бічної поверхні дорівнює 1256 см2.
3. Знайти об’єм циліндра, якщо площа його бічної поверхні дорівнює 3140 см2, а радіус основи — 10 см.
Високий рівень
1. 1) Скласти формулу для обчислення
V — об’єму циліндра за D — діаметром
його основи і h — висотою.
2) За розгорткою циліндра
знайти площу повної його поверхні. Рис.
2. Прямокутник зі сторонами 5 см і 12 см обертається навколо меншої сторони. Обчислити бічну поверхню утвореного циліндра.
3. Довести, що відношення об’єму циліндра, утвореного обертанням прямокутника зі сторонами 3 см і 4 см навколо меншої сторони, до об’єму циліндра, утвореного обертаннм цього прямокутника навколо більшої сторони дорівнює 
.
Варіант 2.
Середній рівень
1. Знайти:
1) площу повної поверхні циліндра, якщо площа його основи дорівнює 9 см2, а площі бічної поверхні — 20 см2;
2) об’єм циліндра, в якого площа основи дорівнює 12,56 дм2, а висота дорівнює 10 дм;
3) площу бічної поверхні циліндра, у якого радіус основи дорівнює 5 см, а висота — 20 см (p» 3).
2. Обчислити об’єм циліндра, в якого радіус основи дорівнює 6 см, а висота — 20 см.
3. Обчислити площу повної поверхні циліндра, в якого радіус основи дорівнює 2 см, а висота — 5 см.
Достатній рівень
1. Обчислити площу повної поверхні і об’єм циліндра, у якого діаметр основи і висота дорівнюють 6 см.
2. Знайти площу основи циліндра, якщо його висота дорівнює 8 см, а площа бічної поверхні дорівнює 251,2 см2.
3. Знайти об’єм циліндра, якщо площа його бічної поверхні дорівнює 1884 см2, а радіус основи — 10 см.
Високий рівень
1. 1) Скласти формулу для обчислення
V — об’єму циліндра за D — діаметром
його основи і b — твірною.
2) За розгорткою циліндра
знайти його об’єм. Рис.
2. Прямокутник зі сторонами 5 см і 4 см обертається навколо більшої сторони. Обчислити бічну поверхню утвореного циліндра.
3. Довести, що відношення об’єму циліндра, утвореного обертанням прямокутника зі сторонами 5 см і 10 см навколо меншої сторони, до об’єму циліндра, утвореного обертаннм цього прямокутника навколо більшої сторони дорівнює 2.
Варіант 3.
Середній рівень
1. Знайти:
1) площу повної поверхні циліндра, якщо площа його основи дорівнює 4 см2, а площі бічної поверхні — 40 см2;
2) об’єм циліндра, в якого площа основи дорівнює 18,26 см2, а висота дорівнює 10 см;
3) площу бічної поверхні циліндра, у якого радіус основи дорівнює 4 см, а висота — 8 см (p» 3).
2. Обчислити об’єм циліндра, в якого радіус основи дорівнює 4 см, а висота — 20 см.
3. Обчислити площу повної поверхні циліндра, в якого радіус основи дорівнює 3 см, а висота — 8 см.
Достатній рівень
1. Обчислити площу повної поверхні і об’єм циліндра, у якого діаметр основи і висота дорівнюють 10 см.
2. Знайти площу основи циліндра, якщо його висота дорівнює 20 см, а площа бічної поверхні дорівнює 628 см2.
3. Знайти об’єм циліндра, якщо площа його бічної поверхні дорівнює 125б6 см2, а радіус основи — 4 см.
Високий рівень
1. 1) Скласти формулу для обчислення
Sn — площі повної поверхні циліндра за D — діаметром
його основи і h — висотою.
2) Знайти площу його
повної поверхні. Рис.
2. Прямокутник зі сторонами 20 см і 5 см обертається навколо більшої сторони. Обчислити площу бічної поверхні утвореного циліндра.
3. Довести, що відношення об’єму циліндра, утвореного обертанням прямокутника зі сторонами 3 см і 12 см навколо більшої сторони, до об’єму циліндра, утвореного обертаннм цього прямокутника навколо меншої сторони дорівнює 
.
Варіант 4.
Середній рівень
1. Знайти:
1) площу повної поверхні циліндра, якщо площа його основи дорівнює 25 см2, а площі бічної поверхні — 100 см2;
2) об’єм циліндра, в якого площа основи дорівнює 36 см2, а висота дорівнює 20 дм;
3) площу бічної поверхні циліндра, у якого радіус основи дорівнює 5 см, а висота — 12 см (p» 3).
2. Обчислити об’єм циліндра, в якого радіус основи дорівнює 5 см, а висота — 10 см.
3. Обчислити площу повної поверхні циліндра, в якого радіус основи дорівнює 4 см, а висота — 12 см.
Достатній рівень
1. Обчислити площу повної поверхні і об’єм циліндра, у якого діаметр основи і висота дорівнюють 12 см.
2. Знайти площу основи циліндра, якщо його висота дорівнює 20 см, а площа бічної поверхні дорівнює 3140 см2.
3. Знайти об’єм циліндра, якщо площа його бічної поверхні дорівнює 628 см2, а радіус основи — 12,5 см.
Високий рівень
1. 1) Скласти формулу для обчислення
V — об’єму циліндра за D — діаметром
його основи і b — твірною.
2) За розгорткою циліндра
знайти його об’єм. Рис.
2. Квадрат із стороною 2 дм обертається навколо сторони. Обчислити об’єм утвореного циліндра.
3. Довести, що відношення об’єму циліндра, утвореного обертанням прямокутника зі сторонами 6 дм і 18 см навколо більшої сторони, до об’єму циліндра, утвореного обертаннм цього прямокутника навколо меншої сторони дорівнює 
.
ТЕМА 21. КУЛЯ
Варіант 1.
Середній рівень
1. Знайти:
1) діаметр кулі, радіус якої 4 м;
2) радіус кулі, діаметр якої 10 см;
3) площину поверхні кулі, радіус якої дорівнює 3 дм (p» 3);
4) об’єм кулі, радіус якої дорівнює 1 дм (p» 3).
2. Обчислити площу поверхні кулі, радіус якої дорівнює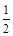 
дм (p» 3,14).
3. Обчислити об’єм кулі, радіус якої дорівнює 2 м 
.
Достатній рівень
1. Обчислити:
1) площу поверхні кулі, діаметр якої дорівнює 1 дм;
2) об’єм кулі, діаметр якої дорівнює 3 см.
2. Знайти відношення об’єму кулі радіуса 1 дм до об’єму кулі радіуса 3 дм.
3. Обчислити площу поверхні і об’єм кулі, довжина великого круга якої дорівнює 12,5 см.
Високий рівень
1. 1) Скласти формулу для обчислення S — поверхні кулі за її D — діаметром.
2) Знайти відношення об’єму кулі діаметра 1 дм до об’єму куба, ребро якого дорівнює 1 дм.
2. Діаметри двох куль, що виготовлені з одного матеріалу дорівнюють 2 дм і 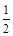дм. У скільки разів маса першої кулі більша від маси другої?
3. Куля діаметра 1 дм міститься всередині куба і дотикається до всіх його граней. У скільки разів об’єм куба більший від об’єма кулі? Відповідь округлити до десятих.
Варіант 2.
Середній рівень
1. Знайти:
1) діаметр кулі, радіус якої 3 м;
2) радіус кулі, діаметр якої 20 см;
3) площину поверхні кулі, радіус якої дорівнює 10 дм (p» 3);
4) об’єм кулі, радіус якої дорівнює 2 дм (p» 3).
2. Обчислити площу поверхні кулі, радіус якої дорівнює 10 см (p» 3,14).
3. Обчислити об’єм кулі, радіус якої дорівнює 1 дм .
Достатній рівень
1. Обчислити:
1) площу поверхні кулі, діаметр якої дорівнює 2 см;
2) об’єм кулі, діаметр якої дорівнює 6 дм.
2. Знайти відношення площі поверхні кулі радіуса 3 см до площі поверхні кулі радіуса 1 см.
3. Обчислити об’єм кулі, довжина великого круга якої дорівнює 6,28 см.
Високий рівень
1. 1) Скласти формулу для обчислення V —об’єму кулі за її D — діаметром.
2) Знайти відношення об’єму кулі діаметра 2 дм до об’єму куба, ребро якого дорівнює 2 дм.
2. Діаметри двох куль, що виготовлені з одного матеріалу дорівнюють 2 дм і 1 дм. У скільки разів маса першої кулі більша від маси другої?
3. Куля діаметра 3 дм міститься всередині куба і дотикається до всіх його граней. У скільки разів об’єм куба більший від об’єма кулі? Відповідь округлити до десятих.
Варіант 3.
Середній рівень
1. Знайти:
1) діаметр кулі, радіус якої 5 м;
2) радіус кулі, діаметр якої 14 см;
3) площину поверхні кулі, радіус якої дорівнює 2 дм (p» 3);
4) об’єм кулі, радіус якої дорівнює 5 см (p» 3).
2. Обчислити площу поверхні кулі, радіус якої дорівнює 1 дм (p» 3,14).
3. Обчислити об’єм кулі, радіус якої дорівнює 7 дм .
Достатній рівень
1. Обчислити:
1) площу поверхні кулі, діаметр якої дорівнює 10 см;
2) об’єм кулі, діаметр якої дорівнює 2 дм.
2. Знайти відношення об’єму кулі радіуса 2 см до об’єма кулі радіуса 4 см.
3. Знайти площу поверхні кулі, довжина великого круга якої дорівнює 31,4 см.
Високий рівень
1. 1) Скласти формулу для обчислення S — поверхні кулі за D — діаметром великого круга.
2) Знайти відношення об’єму кулі діаметра 3 дм до об’єму куба, ребро якого дорівнює 3 дм.
2. Пофарбували дві кулі, радіуси яких дорівнюють 10 дм і 1 дм. На фарбування якої кулі витратили більше фарби і в скільки разів?
3. Куля діаметра 2 дм міститься всередині куба і дотикається до всіх його граней. У скільки разів об’єм куба більший від об’єма кулі? Відповідь округлити до десятих.
Варіант 4.
Середній рівень
1. Знайти:
1) діаметр кулі, радіус якої 14 дм;
2) радіус кулі, діаметр якої 8 см;
3) площину поверхні кулі, радіус якої дорівнює 4 дм (p» 3);
4) об’єм кулі, радіус якої дорівнює 3 дм (p» 3).
2. Обчислити площу поверхні кулі, радіус якої дорівнює 2 дм (p» 3,14).
3.
