3. Знайти спільне кратне чисел 18 і 20, яке більше від 700, але менше від 800.
Високий рівень
1. 1) Знайти найменше спільне кратне чисел 40, 72 і 90.
2) Яблука, що є в корзині можна порівну розділити або між 10 чоловіками, або між 6 чоловіками, або між 8 чоловіками. Скільки яблук в корзині, якщо їх більше ніж 300, але менше, ніж 400?
2. Знайти значення x, якщо НСД (98; x) = 14 і НСК (98; x) = 362.
3. Знайти найменше натуральне число, яке при діленні на 2, на 3, на 5 і на 7 дає остачу 1.
Варіант 3.
Середній рівень
1. Знайти найменше спільне кратне чисел:
1) а) 7 і 13; б) 5 і 6;
2) а) 3 і 36; б) 10 і 40;
3) а) 10 і 15; б) 6 і 14;
4) а) m = 2 × 3 і n = 2 × 11; б) m = 2 × 5 і n = 2 × 5 × 5 × 3.
2. Знайти найменше спільне кратне чисел розкладом їх на прості множники:
а) 34 і 50; б) 50 і 55.
3. Скільки повинно бути найменше груш, щоб їх можна було розділити порівну між 10 чоловіками або 15 чоловіками?
Достатній рівень
1. 1) Знайти найменше спільне кратне чисел: а) m = 22 × 33 і n = 23 × 32 × 5; б) 50 і 440.
2) Крок Петрика дорівнює 60 см, а Андрыйка 80 см. На якій найменшій відстані вони всі зроблять по цілому числу кроків і скільки кроків зробить при цьому кожний з них?
2. Знайти найменше натуральне число, яке ділиться без остачі на 8, 12 і 15.
3. Знайти спільне кратне чисел 15 і 18, яке більше від 700, але менше від 800.
Високий рівень
1. 1) Знайти найменше спільне кратне чисел 56, 76 і 126.
2) Книги, що є в домашній бібліотеці, можна розставити порівну або на 10 полицях, або на 12 полицях, або на 15 полицях. Скільки книг у бібліотеці, якщо їх більше, ніж 200, але менше ніж 250?
2. Числа a × b — взаємно прості.Довести, що НСД (a; b) × НСК (a; b) = a × b.
3. Знайти найменше натуральне число, яке при діленні на 3, на 5, на 7 і на 15 дає в остачі 2.
Варіант 4.
Середній рівень
1. Знайти найменше спільне кратне чисел:
1) а) 5 і 7; б) 7 і 8;
2) а) 11 і 44; б) 9 і 36;
3) а) 12 і 18; б) 9 і 15;
4) а) m = 2 × 3 і n = 2 × 11; б) m = 2 × 17 і n = 2 × 2 × 5.
2. Знайти найменше спільне кратне чисел розкладом їх на прості множники:
а) 14 і 12; б) 30 і 55.
3. Один з велосипедистів проїжджає коло за 9 хв, а другий — за 6 хв. Через який найближчий час після старту вони знову зустрінуться на місці старту?
Достатній рівень
1. 1) Знайти найменше спільне кратне чисел: а) m = 2 × 52 і n = 22 × 3 × 53; б) 24 і 252.
2) Тривалість кінцевого маршруту одного автобуса 1 год 15 хв, а другого — 1 год. Через який найближчий час після одночасного їх виїзду з автостанції вони знову зустрінуться?
2. Знайти найменше натуральне число, яке ділиться без остачі на 8, 10 і 14.
3. Знайти спільне кратне чисел 14 і 18, яке більше від 600, але менше від 700.
Високий рівень
1. 1) Знайти найменше спільне кратне чисел 24, 75 і 45.
2) Рибу, яку зловили рибалки, можна розкласти на купки або по 8, або по 12, або по 15 штук, причому рибин більше, ніж, але менше, ніж. Скільки рибин зловили рибалки?
2. Число a кратне числу b. Довести, що НСД (a; b) × НСК (a; b) = a × b.
3. Знайти найменше натуральне число, яке при діленні на 5, на 7, на 15 і на 20 дає в остачі 3.
Розділ ІІ. ЗВИЧАЙНІ ДРОБИ
ТЕМА 5. ОСНОВНА ВЛАСТИВІСТЬ ДРОБІВ. СКОРОЧЕННЯ ДРОБІВ
Варіант 1.
Середній рівень
1. 1) Скоротити дроби на 2:  .
.
2) Записати нескоротним звичайним дробом: 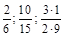 .
.
3) Записати десяткові дроби звичайними і скоротними: 0,5; 0,02; 0,006.
4) Накреслити координатний промінь, взявши за одиничний відрізок 4 клітинки. Записати координати точок  нескоротними дробами і зобразити їх на координатній прямій.
нескоротними дробами і зобразити їх на координатній прямій.
2. Записати нескоротним звичайним дробом: 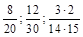 .
.
3. Записати нескоротним звичайним дробом, яку частину становить:
а) 2 хв від 1 години; б) 4 год від 1 доби; в) 20 см від 1 м.
Достатній рівень
1. 1) Записати нескоротним звичайним дробом:  .
.
2) Записати десяткові дроби нескоротними звичайними дробами: 0,48; 0,125.
3) Записати нескоротним дробом, яку частину становить:
а) 36 хв від 1 год; б) 240 м від 1 км.
2. Знайти x, якщо  .
.
3. Записати нескоротним звичайним дробом:  .
.
Високий рівень
1. 1) Записати нескоротним звичайним дробом: а) 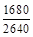 ; б)
; б)  .
.
2) Записати нескоротним звичайним дробом, яку частинустановлять 2,5 см від 1 дм.
2. Знайти x, якщо  :
:
3. Подати нескоротним звичайним дробом вираз  .
.
Варіант 2.
Середній рівень
1. 1) Скоротити дроби на 3:  .
.
2) Записати нескоротним звичайним дробом:  .
.
3) Записати десяткові дроби звичайними і скоротними: 0,2; 0,05; 0,004.
4) Накреслити координатний промінь, взявши за одиничний відрізок 6 клітинок. Записати координати точок 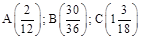 нескоротними дробами і зобразити їх на координатній прямій.
нескоротними дробами і зобразити їх на координатній прямій.
2. Записати нескоротним звичайним дробом: 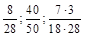 .
.
3. Записати нескоротним звичайним дробом, яку частину становить:
а) 15 хв від 1 години; б) 12 год від 1 доби; в) 200 м від 1 км.
Достатній рівень
1. 1) Записати нескоротним звичайним дробом:  .
.
2) Записати десяткові дроби нескоротними звичайними дробами: 0,96; 0,036.
3) Записати нескоротним дробом, яку частину становить:
а) 24 хв від 1 год; б) 120 г від 1 кг.
2. Знайти x, якщо  .
.
3. Записати нескоротним звичайним дробом:  .
.
Високий рівень
1. 1) Записати нескоротним звичайним дробом: а)  ; б)
; б)  .
.
2) Записати нескоротним звичайним дробом, яку частинустановлять 37,5 см від 1 км.
2. Знайти x, якщо  .
.
3. Подати нескоротним звичайним дробом вираз  .
.
Варіант 3.
Середній рівень
1. 1) Скоротити дроби на 5:  .
.
2) Записати нескоротним звичайним дробом:  .
.
3) Записати десяткові дроби звичайними і скоротними: 0,6; 0,04; 0,002.
4) Накреслити координатний промінь, взявши за одиничний відрізок 8 клітинок. Записати координати точок  нескоротними дробами і зобразити їх на координатній прямій.
нескоротними дробами і зобразити їх на координатній прямій.
2. Записати нескоротним звичайним дробом:  .
.
3. Записати нескоротним звичайним дробом, яку частину становить:
а) 20 хв від 1 години; б) 16 год від 1 доби; в) 2 дм від 1 м.
Достатній рівень
1. 1) Записати нескоротним звичайним дробом:  .
.
2) Записати десяткові дроби нескоротними звичайними дробами: 0,24; 0,056.
3) Записати нескоротним дробом, яку частину становить:
а) 54 хв від 1 год; б) 275 г від 1 кг.
2. Знайти x, якщо 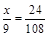 .
.
3. Записати нескоротним звичайним дробом:  .
.
Високий рівень
1. 1) Записати нескоротним звичайним дробом: а) 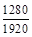 ; б)
; б)  .
.
2) Записати нескоротним звичайним дробом, яку частинустановлять 7,5 см від 1 дм.
2. Знайти x, якщо  .
.
3. Подати нескоротним звичайним дробом вираз  .
.
Варіант 4.
Середній рівень
1. 1) Скоротити дроби на 7: 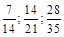 .
.
2) Записати нескоротним звичайним дробом:  .
.
3) Записати десяткові дроби звичайними і скоротними: 0,4; 0,06; 0,005.
4) Накреслити координатний промінь, взявши за одиничний відрізок 10 клітинок. Записати координати точок  нескоротними дробами і зобразити їх на координатній прямій.
нескоротними дробами і зобразити їх на координатній прямій.
2. Записати нескоротним звичайним дробом: 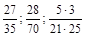 .
.
3. Записати нескоротним звичайним дробом, яку частину становить:
а) 4 хв від 1 години; б) 8 год від 1 доби; в) 20 кг від 1 центнера.
Достатній рівень
1. 1) Записати нескоротним звичайним дробом:  .
.
2) Записати десяткові дроби нескоротними звичайними дробами: 0,12; 0,072.
3) Записати нескоротним дробом, яку частину становить:
а) 48 хв від 1 год; б) 210 г від 1 кг.
2. Знайти x, якщо  .
.
3. Записати нескоротним звичайним дробом:  .
.
Високий рівень
1. 1) Записати нескоротним звичайним дробом: а)  ; б)
; б) 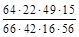 .
.
2) Записати нескоротним звичайним дробом, яку частинустановлять 12,5 кг від 1 т.
2. Знайти x, якщо  .
.
3. Подати нескоротним звичайним дробом вираз  .
.
ТЕМА 6. ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА
Варіант 1.
Середній рівень
1. 1) Звести дроби до знаменника 12: а) 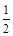 ; б)
; б)  .
.
Звести до найменшого спільного знаменника і порівняти дроби 2)—3):
2)  ; 3)
; 3)  ; 4)
; 4)  .
.
2. Розкласти на прості множники знаменники і звести до найменшого спільного знаменника дроби  .
.
3. Звести до дробу, в якого знаменник розрядна одиниця, і записати десятковими дробами натуральні дроби:  .
.
Достатній рівень
1. 1) Звести до найменшого спільного знаменника і порівняти дроби:  .
.
2) Скільки тридцятих міститься в  ?
?
3) Записати десятковими дробами наступні звичайні дроби: 
2. Звести до найменшого спільного знаменника дроби  .
.
3. Записати усі звичайні дроби із знаменником 10, які більші за дріб  , але менші за дріб
, але менші за дріб  .
.
Високий рівень
1. 1) Звести до найменшого спільного знаменника дроби:  .
.
2) Записати в порядку зростання числа  .
.
3) Через першу трубу басейн заповнюється за 5 год, а через другу — через 4 год. Через яку трубу басейн наповниться водою більше — через першу за 4 год чи через другу за 3 год?
2. Знайти три звичайних дроби, кожний з яких більший від  , але менший від
, але менший від  .
.
3. Знайти дріб із знаменником 10, який більший від  , але менший від
, але менший від  .
.
Варіант 2.
Середній рівень
1. 1) Звести дроби до знаменника 18: а) 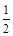 ; б)
; б)  .
.
Звести до найменшого спільного знаменника і порівняти дроби 2)—3):
2)  ; 3)
; 3)  ; 4)
; 4) 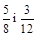 .
.
2. Розкласти на прості множники знаменники і звести до найменшого спільного знаменника дроби  .
.
3. Звести до дробу, в якого знаменник розрядна одиниця, і записати десятковими дробами натуральні дроби:  .
.
Достатній рівень
1. 1) Звести до найменшого спільного знаменника і порівняти дроби:  .
.
2) Скільки шістдесятих міститься в  ?
?
3) Записати десятковими дробами наступні звичайні дроби:  .
.
2. Звести до найменшого спільного знаменника дроби  .
.
3. Записати усі звичайні дроби із знаменником 8, які більші за дріб  , але менші за дріб
, але менші за дріб  .
.
Високий рівень
1. 1) Звести до найменшого спільного знаменника дроби:  .
.
2) Записати в порядку зростання числа  .
.
3) Робітник може виконати завдання за 5 год, а його учень — за 6 год. Хто з них виконає більшу частину завдання — робітник за 4 год чи учень за 5 год?
2. Знайти три звичайних дроби, кожний з яких більший від  , але менший від
, але менший від  .
.
3. Знайти дріб із знаменником 10, який більший від  , але менший від
, але менший від  .
.
Варіант 3.
Середній рівень
1. 1) Звести дроби до знаменника 20: а) 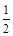 ; б)
; б)  .
.
Звести до найменшого спільного знаменника і порівняти дроби 2)—3):
2) 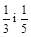 ; 3)
; 3) 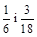 ; 4)
; 4) 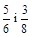 .
.
2. Розкласти на прості множники знаменники і звести до найменшого спільного знаменника дроби  .
.
3. Звести до дробу, в якого знаменник розрядна одиниця, і записати десятковими дробами натуральні дроби:  .
.
Достатній рівень
1. 1) Звести до найменшого спільного знаменника і порівняти дроби: 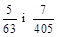 .
.
2) Скільки сотих міститься в  ?
?
3) Записати десятковими дробами наступні звичайні дроби: 
2. Звести до найменшого спільного знаменника дроби  .
.
3. Записати усі звичайні дроби із знаменником 16, які більші від  , але менші від
, але менші від 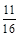 .
.
Високий рівень
1. 1) Звести до найменшого спільного знаменника дроби: 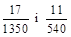 .
.
2) Записати в порядку зростання числа  .
.
3) Перша друкарка може передрукувати рукопис за 7 год, а друга —за 6 год. Яка з друкарок передрукує більше рукопису — перша за 6 год чи друга за 5 год?
2. Знайти три звичайних дроби, кожний з яких більший за 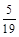 , але менший за
, але менший за  .
.
3. Знайти дріб із знаменником 10, який більший від  , але менший від
, але менший від  .
.
Варіант 4.
Середній рівень
1. 1) Звести дроби до знаменника 24: а) 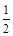 ; б)
; б)  .
.
Звести до найменшого спільного знаменника і порівняти дроби 2)—3):
2)  ; 3)
; 3) 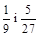 ; 4)
; 4)  .
.
2. Розкласти на прості множники знаменники і звести до найменшого спільного знаменника дроби  .
.
3. Звести до дробу, в якого знаменник розрядна одиниця, і записати десятковими дробами натуральні дроби:  .
.
Достатній рівень
1. 1) Звести до найменшого спільного знаменника і порівняти дроби:  .
.
2) Скільки тридцятих міститься в  ?
?
3) Записати десятковими дробами наступні звичайні дроби: 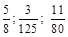
2. Звести до найменшого спільного знаменника дроби  .
.
3. Записати усі звичайні дроби із знаменником 12, які більші від  , але менші від
, але менші від  .
.
Високий рівень
1. 1) Звести до найменшого спільного знаменника дроби: 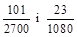 .
.
2) Записати в порядку зростання числа  .
.
3) Легкий автомобіль проїжджає відстань між пунктами А і В за 3 годщ, а вантажний — за 4 год. Хто з них проїде більшу відстань — легковий автомобіль за 2 год чи вантажний за 3 год?
2. Знайти три звичайних дроби, кожний з яких більший за  , але менший за
, але менший за 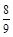 .
.
3. Знайти дріб із знаменником 10, який більший від  , але менший від
, але менший від 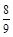 .
.
ТЕМА 7. ДОДАВАННЯ І ВІДНІМАННЯ ЗВИЧАЙНИХ ДРОБІВ
Варіант 1.
Середній рівень
1. Виконати дії:
1)  ; 2)
; 2) 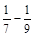 ; 3)
; 3)  ; 4)
; 4)  .
.
2. Тракторист зорав за перший день 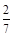 поля, а за другий день
поля, а за другий день  його. Яку частину поля зорав тракторист за два дні?
його. Яку частину поля зорав тракторист за два дні?
3. Розв’язати рівняння  .
.
Достатній рівень
1. 1) Знайти значення виразу  .
.
2) За перший день туристи пройшли  всього шляху, а за другий день
всього шляху, а за другий день  його, а за третій — решту. Яку частину шляху туристи пройшли за третій день?
його, а за третій — решту. Яку частину шляху туристи пройшли за третій день?
2. Розв’язати рівняння  .
.






