2) Перетворити 
у періодичний десятковий дріб і знайти його десяткове наближення до тисячних.
3) Порівняти числа: а) 0,(5) і 0,(51); б) 0,4(3) і 0,(43).
2. Записати у вигляді десяткового дробу суми чисел 
.
3. Способом зрівняння кількості двійок і п’ятірок у знаменнику дробу перетворити у десяткові дроби звичайні дроби: а) 
; б) 
.
Високий рівень
1. 1) Перетворити 
у періодичний десятковий дріб і знайти десяткове наближення до тисячних.
2) Перетворити 
у скінчений десятковий дріб двома способами.
3) Записати у порядку зростання числа: 0,22; 0,(2); 0,2; 0,022; 
.
2. Записати у вигляді періодичного десяткового дробу:
а) 10 × 0,(5); б) 10 × 8,(34); в) 0,(3) + 0,(25).
3. Дано a = 0,(3). Послідовно знайти десяткові записи чисел 10 a і 9 a та записати число a у вигляді звичайного дробу.
Варіант 4.
Середній рівень
1. Перетворити діленнм чисельника на знаменник:
1) 
; 2) 
; 3) 
; 4) 
.
2. Знайти десяткове наближення до сотих чисел: а) 5,(84); б) 
.
3. Порівняти числа: а) і 0,6; б) 0,(7) і 0,7.
Достатній рівень
1. 1) Із дробів 
виписати ті, що перетворюються у:
а) скінченні десяткові дроби; б) нескінченні періодичні десяткові дроби.
2) Перетворити 
у періодичний десятковий дріб і знайти його десяткове наближення до тисячних.
3) Порівняти числа: а) 0,(7) і 0,(74); б) 0,8(1) і 0,(81);
2. Записати у вигляді десяткового дробу суми чисел 
.
3. Способом зрівняння кількості двійок і п’ятірок у знаменнику дробу перетворити у десяткові дроби звичайні дроби: а) 
; б) 
.
Високий рівень
1. 1) Перетворити 
у періодичний десятковий дріб і знайти десяткове наближення до тисячних.
2) Перетворити 
у скінчений десятковий дріб двома способами.
3) Записати у порядку зростання числа: 0,(7); 0,7; 0,777; 0,077;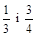 
.
2. Записати у вигляді періодичного десяткового дробу:
а) 10 × 0,(7); б) 10 × 6,(23); в) 0,(3) + 0,(41).
3. Дано a = 0,(5). Послідовно знайти десяткові записи чисел 10 a і 9 a та записати число a у вигляді звичайного дробу.
Розділ І. ВІДНОШЕННЯ І ПРОПОРЦІЇ
ТЕМА 12. ВІДНОШЕННЯ. ВІДСОТКОВЕ ВІДНОШЕННЯ
Варіант 1.
Середній рівень
1. 1) Дано числа 4 і 200. Записати двома способами відношення більшого числа до меншого і обчислити його.
2) Скоротити відношення 35: 14 діленням на найбільший спільний дільник.
3) Замінити відношення 
відношенням натуральних чисел множенням на найменше спільне кратне знаменників.
4) Обчислити відсоткове відношення числа 2 до числа 25.
2. Знайти невідомий член відношення: 1) x: 5 = 8; 2) 
.
3. 1) Обчислити відношення 2 см до 4 м.
2) Обчислити відсоткове відношення 25 г солі до 250 г розчину.
Достатній рівень
1. 1) Відстань між пунктами A і B на карті дорівнює 2 см, а на місцевості 200 км. Знайти масштаб карти (відношення відстані на карті до відстані на місцевості).
2) Розчин містить 150 г води і 20 г солі. Знайти відсотковий вміст солі у розчині.
3) Замінити відношення 
відношенням натуральних чисел.
2. Відношення числа a до числа 50 дорівнює 40%. Знайти число a.
3. Залізна руда містить 40% заліза. Скільки треба добути такої руди, щоб одержати 8 т заліза.
Високий рівень
1. 1) Із чисел 6; 12; 30 і 36 скласти усі відношення менші від 1, і записати їх нескоротними звичайними дробами.
2) До 400 г 10%-го розчину солі добавили 80 г солі. Визначити у відсотках вміст солі у новому розчині.
2. Перше число становить 20% від другого. Скільки відсотків становить друге число від першого.
3. Є 120 г 5%-го розчину солі. Скільки треба добавити до цього розчину води, щоб одержати 2%-ий розчин солі?
Варіант 2.
Середній рівень
1. 1) Дано числа 21 і 3. Записати відношення меншого числа до більшого (двома способами) і його значення нескоротним звичайним дробом.
2) Скоротити відношення 44: 33 діленням на найбільший спільний дільник.
3) Замінити відношення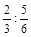 
відношенням натуральних чисел множенням на найменше спільне кратне знаменників.
4) Обчислити відсоткове відношення числа 7 до числа 50.
2. Знайти невідомий член відношення: 1) 
; 2) 40: x = 8.
3. 1) Обчислити відношення 4 хв до 1 год.
2) Обчислити відсоткове відношення 45 г солі до 300 г розчину.
Достатній рівень
1. 1) Відстань між пунктами A і B на карті дорівнює 2 дм, а на місцевості 400 км. Знайти масштаб карти (відношення відстані на карті до відстані на місцевості).
2) Сплав містить 50 г олова і 20 г свинцю. Знайти відсотковий вміст олова усплаві.
3) Замінити відношення відношенням натуральних чисел.
2. Відношення числа 750 до числа b дорівнює 250%. Знайти число b.
3. Квасоля містить 20% білка. Скільки грамів білка міститься у 800 г квасолі?
Високий рівень
1. 1) Із чисел 3; 9; 12 і 21 скласти усі відношення менші від 1, і записати їх нескоротними звичайними дробами.
2) До 200 г 10%-го розчину солі добавили 50 г води. Визначити у відсотках вміст солі у новому розчині.
2. Перше число становить 25% від другого. Скільки відсотків становить друге число від першого.
3. Є 400 г 15%-го розчину солі. Скільки треба добавити до цього розчину води, щоб одержати 2%-ий розчин солі?
Варіант 3.
Середній рівень
1. 1) Дано числа 6 і 240. Записати двома способами відношення більшого числа до меншого і обчислити його.
2) Скоротити відношення 25: 35 діленням на найбільший спільний дільник.
3) Замінити відношення 
відношенням натуральних чисел множенням на найменше спільне кратне знаменників.
4) Обчислити відсоткове відношення числа 3 до числа 20.
2. Знайти невідомий член відношення: 1) 
; 2) 60: x = 5.
3. 1) Обчислити відношення 6 г до 2 кг.
2) 40 т залізної руди містить 24 т заліза. Визначити у відсотках вміст заліза у руді.
Достатній рівень
1. 1) Довжина будинку на плані масштаб якого 1: 200, дорівнює 25 см. Чому дорівнює довжина будинку на місцевості?
2) Сплав містить 80 г магнію і 120 г алюмінію. Визначити відотковий вміст магнію у сплаві.
3) Замінити відношення відношенням натуральних чисел.
2. Відношення числа a до числа 70 дорівнює 30%. Знайти число a.
3. При помелі жита виходить 75% борошна. Скільки потрібно взяти жита, щоб одеожати 12 кг борошна?
Високий рівень
1. 1) Із чисел 4; 12; 20 і 28 скласти усі відношення менші від 1, і записати їх нескоротними звичайними дробами.
2) До 400 г 5%-го розчину солі добавили 100 г води. Визначити у відсотках вміст солі у новому розчині.
2. Перше число становить 125% від другого. Скільки відсотків становить друге число від першого.
3. Є 300 г сплаву міді і олова, в якому 60% міді. Скільки потрібно добавитив цей сплав олова, щоб одержати сплав, в якому 45% міді?
Варіант 4.
Середній рівень
1. 1) Дано числа 30 і 2. Записати відношення меншого числа до більшого (двома способами) і його значення нескоротним звичайним дробом.
2) Скоротити відношення 6: 8 діленням на найбільший спільний дільник.
3) Замінити відношення 
відношенням натуральних чисел множенням на найменше спільне кратне знаменників.
4) Обчислити відсоткове відношення числа 3 до числа 10.
2. Знайти невідомий член відношення: 1) x: 2 = 14; 2) 
.
3. 1) Обчислити відношення 4 год до 2 діб.
2) 20 кг картоплі містить 4 кг грохмалю. Знайти відсотковий вміст крохмалю у картоплі.
Достатній рівень
1. 1) Масштаб плану 1: 500. Яка віддаль на місцевості, якщо на плані вона становить 4 см?
2) Сплав містить 24 кг міді і 16 кг цинку. Знайти у відсотках вміст міді у сплаві.
3) Замінити відношення відношенням натуральних чисел.
2. Відношення числа 70 до числа a дорівнює 120%. Знайти число a.
3. Картопля містить 20% крохмалю. Скільки крохмалю одержать з 15 кг такої картоплі?
Високий рівень
1. 1) Із чисел 5; 15; 20 і 35 скласти усі відношення менші від 1, і записати їх нескоротними звичайними дробами.
2) До 200 г 5%-го розчину солі добавили 40 гсолі. Визначити у відсотках вміст солі у новому розчині.
2. Перше число становить 250% від другого. Скільки відсотків становить друге число від першого.
3. Є 600 г сплаву алюмінію і магнію, в якому 30% алюмінію. Скільки потрібно добавити до цього сплаву алюмінію, щоб одержати сплав, в якому 40%?
ТЕМА 13. ПРОПОРЦІЇ
Варіант 1.
Середній рівень
1. 1) Із відношень 14: 28; 14: 3; 14: 21 вказати те, що утворює пропорцію з відношенням 2: 3 і записати її.
Знайти невідомий член пропорції (2)—4)):
2) x: 6 = 5: 2, використавши основну властивість пропорцій;
3) x: 7 = 15: 3, обчисливши праве відношення;
4) 
, скоротивше праве відношення.
Розв’язати рівняння використавши основну властивість пропорції (2 — 3):
2. 
.
3. 
.
Достатній рівень
1. Знайти двома способами невідомий член пропорції 6: x = 15: 0,5.
2. Розв’язати рівняння 
.
3. Скласти чотири пропорції, використавши рівність 3 × 8 = 6 × 4.
Високий рівень
1. 1) Із чисел 44; 4; 11 і 12 скласти чотири пропорції.
2) Розв’язати рівняння 3: (4 x – 3) = 25: 16, використавши основну властивість пропорцій.
2. Довести основну властивість пропорції: якщо 
, то ad = bc.
Вказівка. Вибрати такий добуток двох із даних чотирьох чисел a, b, c і d, щоб при множенні на нього обох частин пропорції вона перетворилася у рівняння, що доводять.
3. Дано три числа 6, 10 і 12. Знайти таке четверте число, щоб з чисел можна було скласти правильну пропорцію (знайти всі розв’язки задачі).
Варіант 2.
Середній рівень
1. 1) Із відношень 8: 6; 15: 20; 9: 4 вказати те, що утворює пропорцію з відношенням 3: 4 і записати її.
Знайти невідомий член пропорції (2)—4)):
2) x: 8 = 3: 2, використавши основну властивість пропорцій;
3) x: 4 = 36: 12, обчисливши праве відношення;
4) 
, скоротивше праве відношення.
Розв’язати рівняння використавши основну властивість пропорції (2 — 3):
2. 
.
3. 
.
Достатній рівень
1. Знайти двома способами невідомий член пропорції 12: 0,4 = x: 7.
2. Розв’язати рівняння 
.
3. Скласти чотири пропорції, використавши рівність 12 × 15 = 36 × 5.
Високий рівень
1. 1) Із чисел 3; 4; 9 і 12 скласти чотири пропорції.
2) Розв’язати рівняння 3: (2 x – 3) = 50: 17, використавши основну властивість пропорцій.
2. Довести, що коли для чисел a, b, c і d використовується рівняння ad = bc, то вони утворюють пропорцію .
Вказівка. Поділити обидві частини рівності ad = bc на такий добуток двох чисел із даних чотирьох a, b, c і d, щоб утворились пропорції.
3. Дано три числа 5, 10 і 12. Знайти таке четверте число, щоб з чисел можна було скласти правильну пропорцію (знайти всі розв’язки задачі).
Варіант 3.
Середній рівень
1. 1) Із відношень 9: 2; 18: 4; 10: 45 вказати те, що утворює пропорцію з відношенням 2: 9 і записати її.
Знайти невідомий член пропорції (2)—4)):
2) x: 9 = 10: 3, використавши основну властивість пропорцій;
3) x: 11 = 6: 2, обчисливши праве відношення;
4) 
, скоротивше праве відношення.
Розв’язати рівняння використавши основну властивість пропорції (2 — 3):
2. 
.
3. 
.
Достатній рівень
1. Знайти двома способами невідомий член пропорції x: 4 = 27: 0,9.
2. Розв’язати рівняння 
.
3. Скласти чотири пропорції, використавши рівність 8 × 125 = 20 × 50.
Високий рівень
1. 1) Із чисел 7; 45; 35 і 9 скласти чотири пропорції.
2) Розв’язати рівняння 5: (2 x + 3) = 3: 8, використавши основну властивість пропорцій.
2. Довести, що коли ab = cd, то числа a, b, c і d утворюють пропорцію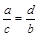 
.
3. Дано три числа 8, 9 і 12. Знайти таке четверте число, щоб з чисел можна було скласти правильну пропорцію (знайти всі розв’язки задачі).
Варіант 4.
Середній рівень
1. 1) Із відношень 21: 9; 7: 3; 15: 35 вказати те, що утворює пропорцію з відношенням 3: 7 і записати її.
Знайти невідомий член пропорції (2)—4)):
2) x: 12 = 3: 2, використавши основну властивість пропорцій;
3) x: 7 = 5: 10, обчисливши праве відношення;
4) 
, скоротивше праве відношення.
Розв’язати рівняння використавши основну властивість пропорції (2 — 3):
2. 
.
3. 
.
Достатній рівень
1. Знайти двома способами невідомий член пропорції 8: x = 0,4: 0,01.
2. Розв’язати рівняння 
.
3. Скласти чотири пропорції, використавши рівність 4 × 15 = 6 × 10.
Високий рівень
1. 1) Із чисел 3; 8; 18 і 48 скласти чотири пропорції.
2) Розв’язати рівняння 2: 15 = 7: (50 y – 16), використавши основну властивість пропорцій.
2. Довести основну властивість пропорції: якщо числа a, b, c і d утворюють пропорцію 
, то ac = bd.
3. Дано три числа 16, 4 і 10. Знайти таке четверте число, щоб з чисел можна було скласти правильну пропорцію (знайти всі розв’язки задачі).
ТЕМА 14. ПРЯМА І ОБЕРНЕНА ПРОПОРЦІЙНІСТЬ.
ПРОПОРЦІЙНИЙ ПОДІЛ
Варіант 1.
Середній рівень
1. 1) За 9 кг товару заплатили 45 грн. Скільки коштують 36 кг цього товару?
2) Число 35 поділити у відношенні 3: 4.
2. 30% числа дорівнюють 27. Знайти 40% цього числа.
3. 4 однакові труби наповнюють басейн за 6 год. За який час наповнять басей 3 такі труби.
Достатній рівень
1. 1) Із 40 кг картоплі одержують 6,8 кг крохмалю. На скільки більше кілограм крохмалю одержуть із 60 кг картоплі.
2) Швидкість поїзда 12 м/с. Знайти його швидкість у км/год.
3) Сплав складається з міді, цинку, нікелю, маси яких відносяться як 4: 5: 6. Скільки кожного металу в сплаві, якщо його маса 1,75 кг.
2. Витрачаючи на виготовлення кожної деталі 40 хв, бригада випускала 540 деталей за зміну. На скільки деталей більше випускатиме бригада за зміну, якщо на виготовлення однієї деталі витрачатиме 36 хв?
3. До обіду зорали 28 га поля, що складає 24% площі поля. Після обіду зорали ще 21 га. Скільки відсотків поля зорали за день?
Високий рівень
1. 1) За 10 робочих днів бригада лісорубів, у складі якої 15 чоловік заготовила 600м3 деревини. Скільки деревини заготує бригада з 12 чоловік за 12 днів при тій же продуктивності праці одного чоловіка.
2) Поділити число 21 на дві частини, які обернено пропорційні до чисел 
.
2. Майстер виготовляє одну деталь за 10 хв, а учень – за 15 хв. Працюючи разом вони виготовили 75 деталей. Скільки деталей виготовив майстер і скільки учень?
3. Сторони трикутника a, b і c відповідно відносяться a: b = 2: 1 і b: c = 3: 4. Знайти довжину сторін трикутника, якщо його периметр дорівнює 34 см.
Варіант 2.
Середній рівень
1. 1) На пошиття 10 однакових костюмів витратили 20 м тканини. Скільки таких костюмів можна пошити з 80 м тканини?
2) Число 45 поділити у відношенні 4: 5.
2. 40% числа дорівнюють 28. Знайти 30% цього числа.
3. Самоскид вантажністю 4 т перевезе вантаж за 10 рейсів. За скільки рейсів перевезе цей вантаж самоскид вантажністю 8 т?
Достатній рівень
1. 1) З 12 кг бавовняного насіння дістали 2,7 кг масла. Скільки кілограмів масла одержуть з 16 кг насіння?
2) Швидкість автомобіля 72 км/год. Знайти його швидкість у м/сек.
3) Сторони трикутника відносяться, як 3: 4: 6. Знайти довжину кожної сторони трикутника, якщо його периметр дорівнює 65 см.
2. Витрачаючи на виготовлення однієї деталі 20 хв, робітник виготовив за зміну 6 деталей. На скільки деталей більше виготовив за зміну робітник, якщо одну деталь він буде виготовляти за 18 хв?
3. До привалу туристи пройшли 16 км, що складає 32%всього маршруту. Після привалу вони пройшли ще 10 км. Скільки відсотків відсотків маршруту пройшли туристи за день?
Високий рівень
1. 1) Для 20 коней на 15 днів запасли 2 т вівса. На скільки днів вистачило 500 кг вівса для 5 коней?
2) Поділити число 170 на дві частини, які обернено пропорційні до чисел 
.
2. Один робітник виконує норму за 4 год, а другий — за 5 год. Працюючи разом, вони виготовили 45 деталей. Скільки деталей виготовив кожен робітник?
3. Знайти числа a, b і c, якщо відомо, що a: b = 7: 15 і b: c = 5: 3, а сума чисел с і a дорівнює 96.
Варіант 3.
Середній рівень
1. 1) За 4 год пліт проплив по річці 20 км. Скільки кілометрів пропливе пліт за 6 год?
2) Число 33 поділити у відношенні 3: 8.
2. 26% числа дорівнюють 130. Знайти 65% цього числа.
3. 4 робітники можуть виконати деяку роботу за 9 год. За скільки годин виконають цю роботу 6 робітників?
Достатній рівень
1. 1) Маса 10 л гасу 8,2 кг. На скільки кілограмів більша маса 35 л гасу?
2) Швидкість руху тіла 5 м/сек. Виразити її у км/год.
3) Маса трьох кульок відноситься, як 2: 7: 8. Знайти масу кожної кульки, якщо їх загальна маса дорівнює 680 г.
2. Чотири насоси заповнюють басейн за 12 год. На скільки швидше заповнять басейн 6 таких насосів?
3. За перший день хлопчик прочитав 34 сторінки, що складає 17% усієї книги. Другого дня він прчитав ще 50 сторінок. Скільки відсотків сторінок книги прочитав учень за два дні?
Високий рівень
1. 1) Шість туристів на 3 дні походу взяли 12 кг картоплі. Скільки картоплі повинні взяти 4 туристи на 9 днів походу при тій же нормі на людину?
2) Поділити число 230 на дві частини, які обернено пропорційні до чисел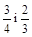 
.
2. Одна друкарка друкує сторінку за 10 хв, а друга — за 12 хв. Працюючи разом, вони надрукували 220 сторінок рукопису. Скільки сторінок надрукувала кожна з них?
3. Знайти числа a, b і c, якщо відомо, що a: b = 2: 3 і b: c = 4: 5, а сума чисел a і с дорівнює 92.
Варіант 4.
Середній рівень
1. 1) На 6 га ріллі було посіяно 10 ц зерна. Скільки потрібно зерна, щоб засіяти 24 га ріллі?
2) Число 520 поділити у відношенні 8: 5.
2. 20% числа дорівнюють 17. Знайти 80% цього числа.
3. На 4 верстатах деяку роботу можна виконати за 12 днів. За скільки днів можна виконати цю роботу на 8 таких верстатах?
Достатній рівень
1. 1) 200 г розчину містить 10 г солі. На скільки грам повинно бути більше розчину, щоб в ньому було 35 г солі?
2) Швидкість руху тіла 150 м/хв. Виразити її у км/год.
3) Маса двох кульок відноситься, як 11: 3. Знайти загальну масу кульок, якщо різниця дорівнює 720 г.
2. Затрачаючи на виготовлення кожної деталі 25 хв, перший робітник виготовив за зміну 300 деталей. На скільки більше часу затрачав на виготовлення однієї деталі другий робітник, якщо за зміну він виготовив 250 деталей?
3. До обіду робітник виготовив 17 деталей, що складає 34% усього завдання. Після обіду робітник виготовив ще 15 деталей. Скільки відсотків усього завдання виконав робітник за перший день?
Високий рівень
1. 1) Бригада з 16 чоловік за 10 днів зібрала 90 т картоплі. За скільки днів збере бригада з 12 чоловік 80 т картоплі, якщо буде працювати з такоюж продуктивністю?
2) Поділити число 290 на дві частини, які обернено пропорційні до чисел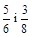 
.
2. Перший робітник виготовляє за 6 хв, а другий — за 10 хв. Працюючи разом, вони виготовили 52 деталі. Скільки деталей виготовив кожний з робітників?
3. Знайти числа a, b і c, якщо відомо, що a: b = 2: 3 і b: c = 4: 7, а сума чисел a і b дорівнює 60.
