1) спецификация модели;
2) сбор статистической информации об объекте-оригинале в виде конкретных значений экзогенных и эндогенных переменных, включенных в спецификацию модели;
3) оценка параметров модели (настройка, оценивание или идентификация модели);
4) проверка адекватности модели (проверка соответствия настроенной модели объекту-оригиналу).
70. Теорема Гаусса – Маркова.
Постановка задачи:
Имеем случайную выборку наблюдений за поведением экономического объекта объемом n
Выборка наблюдений за переменными модели 
Первый индекс – номер регрессора
Второй индекс – номер наблюдения
(7.2)
(7.2) - Система уравнений наблюдений, связывающая наблюдения в выборке
Сформируем вектора и матрицу коэффициентов на основе системы (7.2)
Y – вектор выборочных значений эндогенной переменной
U – вектор выборочных значений случайного возмущения
A - вектор неизвестных параметров модели
х – вектор регрессоров
X – матрица коэффициентов при неизвестных параметрах
По данным выборки найти: Ã, Cov(ÃÃ), σu, σ(ỹ(z))
Теорема (Гаусса – Маркова)
Если матрица Х неколлинеарна и вектор случайных возмущений удовлетворяет следующим требованиям:
Математическое ожидание всех случайных возмущений равно нулю
Дисперсия случайных возмущений постоянна во всех наблюдениях
(условие ГОМОСКЕДАСТИЧНОСТИ)
Случайные возмущения в разных наблюдениях не зависимы
Случайные возмущения и регрессоры не зависимы
Тогда наилучшей линейной процедурой оценки параметров модели (7.1) является:
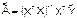(7.3)
которая удовлетворяет методу наименьших квадратов
При этом:
Доказательство
Воспользуемся методом наименьших квадратов
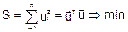(7.4)
где
(7.5)
Подставив (7.5) в (7.4) получим
(7.6)
Для получения необходимого условия экстремума дифференцируем (7.6) по вектору параметров
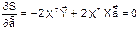Откуда система нормальных уравнений для определения искомых параметров получает вид
(7.7)
Решение системы (7.7) в матричном виде есть
Выражение (7.3) доказано
Докажем несмещенность оценок (7.3)
есмещенность оценки (7.3) доказана
Вычислим ковариационную матрицу оценок (7.3)
В результате получено выражение (7.4)
71. Тест Дарбина – Уотсона, последовательность его выполнения.
Тест Дарбина - Уотсона позволяет проконтролировать некоррелированность случайных возмущений. Он предназначен для проверки предпосылки теоремы Гаусса – Маркова (H0: Cov (ui,uj) = 0 при j=i-1).
Последовательность действий:
1) По уравнениям наблюдений объекта следует вычислить МНК-оценки и оценки случайных остатков;
2) Вычислить величину DW = По формуле 
вычисляется
3) Из таблицы Дарбина и Уотсона следует выбрать две величины dl и du
4) Проверить, в какое из 5 множеств интервала (0;4) попала величина DW. Если значение статистики DW попало в интервал (dl;du), то сделать определенный вывод не возможно. Если в интервале (du;2), то случайные возмущения не имеют автокорреляции. Если в интервале (0;dl), то случайные возмущения имеют положительную автокорреляцию. Если в интервале (4-dl;4), то случайные возмущения имеют отрицательную автокорреляцию.
Тест Стьюдента.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей.
Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т.е. определяют фактическое значение t-критерия Стьюдента
где m b – стандартная ошибка параметра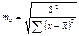 
, где S - остаточная дисперсия на одну степень свободы
Данный критерий затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2). Этот же результат можно получить после извлечения корня из F-критерия, т.е. tb=√F. Аналогично для параметра а.
Фактическое значение t-критерия Стьюдента определяется как
Данная формула свидетельствует о том, что в парной линейной регрессии t2r=F. Кроме того t2b=F, следовательно, t2r= t2b. Таким образом проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о значимости линейного уравнения регрессии.
73. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей.
По отношению к выбранной спецификации модели, все экономические переменные объекта подразделяются на два типа: эндогенные и экзогенные.
Экзогенные – экон-кие переменные, значения которых определяются вне данной модели.
Эндогенные – экон-ские переменные, значения которых определяются внутри данной модели.
Лаговые – переменные, датированные предыдущими моментами времени и находящиеся в ур-нии с текущ переменными.
Фиктивные - переменные, учитывающие в моделях влияние качественных факторов.
Замещающая - переменная, тесно коррелирующая с регрессором, который не поддается наблюдению.
Инструментальная - переменные, с помощью которых устраняется нарушение 4 предпосылки теоремы Гаусса-Маркова (устранить влияние корреляции случайных возмущений).
Предопределённые переменные – это экзогенные и лаговые.
Приведенная - форма спецификации эконометрической модели, в которой значения текущих эндогенных переменных всегда выражены в виде явных функций предопределенных переменных.
Структурная - форма спецификации эконометрической модели, полученная в результате математической формализации экономических закономерностей.
При помощи алгебраических преобразований модель от структурной формы может быть трансформирована к приведенной форме, где каждая эндогенная переменная представляется в виде явной функции только экзогенных переменных модели.
