В моделях, нелинейных по параметрам, например степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование.
Логарифмические модели. Степенные зависимости между переменными широко распространены в практике эконометрического моделирования социально-экономических процессов. Рассмотрим уравнение парной регрессии вида
Y = AXb где А и b— параметры модели.
Линеаризуем:
прологарифмируем обе части данного уравнения: ln(Y)=ln(A) + b*ln(X) = a+ b*ln(X), где а= ln(A) (*)
Спецификация, соответствующая (*) называется двойной логарифмической моделью:
ln(Y)= a+ b*ln(X)+u,
поскольку и эндогенная переменная, и регрессор используются в логарифмической форме.
Введем обозначения: Y*=ln(Y), X*=ln(X)
Y*=a+b*X+u
Получаем спецификацию линейной модели, к которой при соответствующем включении случайного возмущения применим МНК.
В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия  min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е.ln y, 1/y. Так, в степенной функции
min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е.ln y, 1/y. Так, в степенной функции 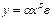 МНК применяется к преобразованному уравнению lny = lnα + β ln x ln ε. Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах.
МНК применяется к преобразованному уравнению lny = lnα + β ln x ln ε. Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах.  Соответственно если в линейных моделях
Соответственно если в линейных моделях  то в моделях, нелинейных по оцениваемым параметрам,
то в моделях, нелинейных по оцениваемым параметрам,  . Вследствие этого оценка параметров оказываются несколько смещенной.
. Вследствие этого оценка параметров оказываются несколько смещенной.
Пусть получена МНК-оценка моделиY*=a+b*X+u:
y*=ā + bx+u
(Sā) (Sb) (Su)
Коэффициенты исходной модели и их стандартные ошибки вычисляются с учетом замены по формулам:
А^=exp(ā)
SĀ= А^*Sā
Se, Sb̄, b̄ - такие же
Нелинейный МНК:
В общем случае оценка нелинейных по параметрам уравнений выполняется с помощью так называемого нелинейного метода наименьших квадратов (НМНК).
Обозначим нелинейное по параметрам уравнение регрессии f(X, ß) (X— матрица рсгрсссоров,ß — вектор параметров). Параметры уравнений в данном методе подбираются таким образом, чтобы максимально приблизить кривую f(X, ß) к результатам
наблюдений эндогенной переменной Y. Таким образом, здесь, как и в обычном
МНК, минимизируется сумма квадратов отклонений:
F=  2 (**)
2 (**)
Если продифференцировать F по параметрам и приравнять производные нулю, то получим нелинейную систему нормальных уравнений. В случае линейного уравнения регрессии нормальные уравнения представляли собой систему линейных уравнений, решение которой не составляло труда.
Нелинейный метод наименьших квадратов сводится к задаче минимизации функции (**) нескольких переменных ß=(ß1,…,ßn)






