Фиктивной переменной наз-ся атрибутивный или качественный фактор, представленный посредством определённого цифрового кода.
Наиболее наглядным примером применения фиктивных переменных является модель регрессии, отражающая проблему разрыва в заработной плате у мужчин и женщин.
Предположим, что на основе собранных данных была построена модель регрессии, отражающая зависимость заработной платы рабочих y от их возраста х: yt=β0+β1xt.
Однако данная модель регрессии не может в полной мере охарактеризовать вариацию результативной переменной. Поэтому в модель необходимо ввести дополнительный фактор, например пол, на основании предположения о том, что у мужчин в среднем заработная плата выше, чем у женщин. В связи с тем, что переменная пола является качественной, её необходимо представить в виде фиктивной переменной следующим образом:
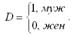
С учётом новой фиктивной переменной модель регрессии примет вид: y=β0+β1x+β2D,
где β2 – это коэффициент, который характеризует в среднем разницу в заработной плате у мужчин и женщин.
Моделью регрессии с переменной структурой называется модель регрессии, которая включает в качестве факторной переменной фиктивную переменную.
Рассмотрим модель регрессии, характеризующую зависимость переменной размера заработной платы у от переменной стажа работников х с различным образованием. Качественная переменная «образование» может принимать три значения: среднее, среднее специальное и высшее. Для включения факторной переменной «образование» в модель регрессии, необходимо ввести две новых фиктивных переменных, потому что их количество должно быть на единицу меньше, чем значений качественной переменной.
Следовательно, качественная переменная «образование» может быть представлена в виде:

Модель регрессии, характеризующая зависимость переменной размера заработной платы у от переменной стажа работников х с различным образованием, примет вид: y=β0+β1x+β2D1+ β3D2.
Моделью регрессии без ограничений называется модель регрессии, в которую включены все фиктивные переменные.
Базисной моделью или регрессией с ограничениями называется модель регрессии, в которой все значения фиктивных переменных равны нулю.
Для нашего примера модель регрессии вида y=β0+β1x+β2D1+β3D2будет являться моделью регрессии без ограничений, а модель регрессии вида y=β0+β1x при D1= D2=0 будет являться моделью регрессии с ограничениями. Базисная модель регрессии соответствует регрессионной зависимости заработной платы рабочих со средним образованием от стажа работы.
Для модели регрессии без ограничений можно также построить частные регрессии. Например, частная модель регрессии переменной заработной платы работников со средним специальным образованием от переменной стажа: y=β0+β1x+β2D1,
где β2 — это коэффициент, который характеризует, насколько большую заработную плату получают рабочие со средним специальным образованием по сравнению с работниками со средним образованием при одинаковом стаже работы.
Частная модель регрессии переменной заработной платы работников с высшим образованием от переменной стажа: y=β0+β1x+β3D2, где β3 – это коэффициент, который характеризует, насколько большую заработную плату получают рабочие с высшим образованием по сравнению с рабочими со средним образованием при одинаковом стаже работы.
Оценки неизвестных коэффициентов моделей регрессии с переменной структурой рассчитываются с помощью классического метода наименьших квадратов.






