При нарушении гомо-сти и наличии автокорреляции ошибок рекомендуется традиционный МНК заменять обобщенным методом.
ОМНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Остановимся на использовании ОМНК для корректировки гетероскедастичности.
Пусть среднее значение остаточных величин равно нулю. А вот дисперсия их не остается неизменной для разных значений фактора, а пропорциональна величине Ki, т. е.: σ2εi =σ2 *K i, где σ2εi – дисперсия ошибки при конкретном i -м значении фактора; σ2– постоянная дисперсия ошибки при соблюдении предпосылки о гомо-сти остатков; Ki – коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии. При этом предполагается, что σ2 неизвестна, а в отношении величин Ki выдвигаются определенные гипотезы, характеризующие структуру гетеро-сти.
В общем виде для уравнения yi =a+bxi +εi при σ2εi =σ2 *K i модель примет вид: yi =a+bxi +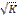 
iεi. В ней остаточные величины гетеро-ны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомо-ми остатками, поделив все переменные, зафиксированные в ходе i -го наблюдения, на 
i. Тогда дисперсия остатков будет величиной постоянной, т. е. σ2εi =σ2. Иными словами, от регрессии y по x мы перейдем к регрессии на новых переменных: y/ 
и x/ 
. Уравнение регрессии примет вид:
,
а исходные данные для данного уравнения будут иметь вид:
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные y и x взяты с весами 1/ 
. Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному МНК, для которого необходимо минимизировать сумму квадратов отклонений вида:
Соответственно получим следующую систему нормальных уравнений:
Если преобразованные переменные x и y взять в отклонениях от средних уровней, то коэффициент регрессии b можно определить как:
При обычном применении МНК к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии b определяется по формуле:
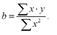
Как видим, при использовании ОМНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весом 1/K.
Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии.
