Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
– факторы, формирующие тенденцию ряда;
– факторы, формирующие циклические колебания ряда;
– случайные факторы.
При различных сочетаниях этих факторов в изучаемом процессе или явлении зависимость уровней ряда от времени может быть различной. Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель, однако в совокупности они формируют его возрастающую или убывающую тенденцию.
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, т.к. экономическая деятельность ряда отраслей экономики зависит от времени года (цены на сельхозпродукцию летом ниже, чем зимой; уровень безработицы в курортных городах зимой выще, чем летом). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой бизнес-цикла, в которой находится экономика страны.
Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты.
Очевидно, что реальные данные содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда.
Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.
Последовательность значений X(t) представляет собой значения случайной величины Х(t), а семейство таких случайных величин представляет собой случайный процесс.
Основными характеристиками случайного процесса являются:
математическое ожидание;
дисперсия;
автокорреляционная функция.
В каждый момент времени t случайный процесс может иметь ряд значений, образующих вектор значений процесса Х(t)
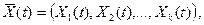(1)
где k – число реализаций этого процесса.
Вектор X(t) называется сечением процесса X(t) в момент времени t. Сечение процесса – случайная величина.
Математическое ожидание процесса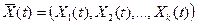 
есть неслучайная функция
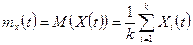(2)
Дисперсией случайного процесса называют неслучайную функцию
Dx(t) = M[X(t) – mx(t)] 2 (3)
Автокорреляционная функция (АКФ)
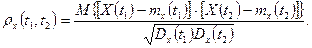
АКФ является коэффициентом корреляции между двумя сечениями процесса Х(t1) и Х(t2). Поэтому |r(t1,t2)| ≤ 1, причем r(t1,t1) = r(t2,t2) = 1.
Случайные процессы делятся на стационарные и нестационарные. Для стационарного процесса математическое ожидание и дисперсия должны быть постоянными величинами, а АКФ должна зависеть только от расстояния между значениями аргументов t1 и t2, а не от места расположения этих значений.
Чтобы найти АКФ, вычисляют коэффициенты корреляции ri между рядами Х(t); t = i, i+1,…, n и X(t-i); t = 1, 2, …, n-i.
Значения ri, нанесенные на плоскость с осями i и r исоединенные ломаной, называют коррелограммой.
Запишем рабочую формулу для расчета ri.
Пусть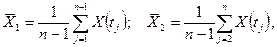 
тогда
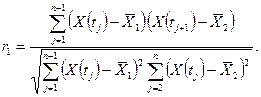
После упрощений получаем
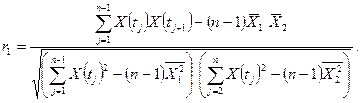
В случае запаздывания на l шагов по времени имеем
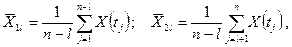
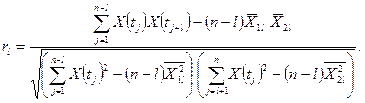
Заметим, что с увеличением запаздывания l объем выборки, по которой вычисляется rl, уменьшается и равен n – l. При небольших n это приведет к тому, что лишь большие по абсолютной величине значения rl будут значимыми (например, при n =12 и уровне значимости α = 0,05 только r1> 0,576 оказывается значимым). Поэтому запаздывания l берут такими, чтобы
n – l было достаточно велико для вычисления значимых rl. На практике обычно берут l ≤ n/4.
После вычисления rl чертится коррелограмма и проводится ее анализ. Интерпретация коррелограмм требует определенного навыка и не всегда легко осуществима.
Для полностью случайного ряда (белого шума) наблюдаются незначимые, малые значения rl, близкие к нулю.
37.Задачи и методы тестирования временных рядов. Состав и содержание основных тестовых гипотез.
Существует два вида временных рядов: моментные и интервальные. Для формирования моментного временного ряда измерение показателей ведется непрерывно, но при обработке используются только те значения, которые соответствуют дискретным моментам времени (например, измерение температуры воздуха каждый час в течение суток). Интервальный временной ряд состоит из значений накапливаемых в определенном интервале времени и фиксируемых по его окончанию (объемы продаж за день, месяц, год). Определение 1. Ряд наблюдений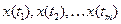 
анализируемой случайной величины 
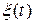произведенных в последовательные моменты времени 
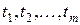$t_1\dots t_m$, называется временным рядом. Отличия временного ряда от последовательности наблюдений:
§ Члены временного ряда, не являются статистически независимыми.
Согласно общей методике анализа временных рядов исходным моментом в построении модели прогнозирования является определение возможности вычленения в структуре ряда его систематической составляющей и, прежде всего трендовой. В связи с этим исследователь должен определить: a)
присутствует ли во временном ряду долговременная тенденция; b)
если тенденция обнаруживается, какой характер она имеет; c)
какие дополнительные закономерности прослеживаются в динамических рядах.
Ответить сразу на все вопросы можно попытаться визуально, проанализировав графическое представление распределения изучаемого показателя во времени, например на экране дисплея компьютера. Этот способ, безусловно, привлекателен, однако также, безусловно, субъективен, так как напрямую зависит от масштаба представления информации на экране, а так же характера восприятия этой информации субъектом.
Другим вариантом является метод исчисления последовательных разностей в уровнях исследуемого ряда. Расчет ведется пока разности практически не сравняются. В этом случае порядок исчисляемых разностей принимается за степень аппроксимирующего полинома. Однако понятно, что основным недостатком названного подхода является возможность подбора кривой описываемой только лишь многочленами, что мало привлекательно для практических исследований. В некоторых случаях, при исследовании временного ряда на наличие долговременных тенденций, полезным может оказаться изучение не только абсолютного цепного прироста, но и абсолютных ускорений в ряду.
Однако наиболее распространенным в практике тестирования рядов на наличие тенденций является использование статистической проверки гипотез о неизменности тенденций по ряду. Если формулировать более строго следует проверить ряд на случайность распределения. Наиболее часто используемыми в этих целях являются: t-критерий, критерий Аббе, критерий серий, основанный на медиане выборки, критерий «восходящих» и «нисходящих» серий, смежный с последним метод Фостера-Стюарта и др [3, 31, 32, 49, 56, 70].
Проверка гипотезы о постоянстве средних значений ряда на основе t-критерия Стьюдента
Процедура проверки гипотезы о постоянстве средних значений по двум выборкам ряда определяется предположением относительно дисперсии распределения. Пусть имеются две выборки: и. Предполагаем, что они получены из одной и той же генеральной совокупности. Проверим гипотезу о равенстве средних по выборкам (иногда гипотеза формулируется, как равенства нулю разницы между средними). На практике для проверки гипотезы о двух средних нормальных генеральных совокупностей используется t-критерий Стьюдента. Однако математические выражения для вычисления t-критерия будут различны при различных гипотезах относительно имеющиеся данных о дисперсии по выборкам [3, 23, 31, 39, 40, 49 и др.].
Для общего описания проверочных и расчетных статистик введем следующие общие обозначения. Пусть
, - математические ожидания и дисперсии величины х генеральных совокупностей соответственно i=1,2;
- заданную постоянную величину;
, - выборочные средние и дисперсии;
- число степеней свободы;
ni – величина I-й выборки;
H0 – формулировка основной тестовой гипотезы;
Факторы, влияющие на формирование значений временного ряда:
А. Долговременные факторы(тренд). Формируют общую тенденцию в изменениях анализируемого признака (долговременная перспектива).
B. Сезонныефакторы. Формируют периодически повторяющиеся в определенные промежутки времени (месяц, неделя, квартал) колебания анализируемого признака, результаты действия описываются периодической функцией.
C. Циклические факторы. Формируют изменения анализируемого признака, обусловленные действием долговременных циклов (выборы, солнечные циклы, демографические циклы, экономические циклы).
D. Случайные факторы. Не регулируемые, их воздействие обуславливает стохастическую природу временного ряда.
Случайное воздействие может быть:
§ Внезапное (разладочное), которое приводит к изменению трендов, циклов и т.д.
§ Эволюционное - незначительное отклонение от постоянной составляющей временного ряда.
Таким образом, временной ряд представим в следующем виде:
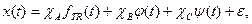(1)
где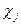 
- индикатор появления соответствующего фактора, j = {A, B, C}.
