При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значений X. Поэтому для регрессии, построенной по МНК, абсолютные величины отклоненийεiи значения хiбудут коррелированны.
Значения хiиεiранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
где di— разность между рангами хiиεi,i= 1, 2,..., п;
п — число наблюдений.
Например, если х20является 15 по величине среди всех наблюдений, аε20 – 21, то d20 = 15-21= - 6.
Если коэффициент корреляции 
для генеральной совокупности равен нулю, то статистика
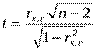
имеет распределение Стьюдента с числом степеней свободы v=n-2. Следовательно, если наблюдаемое значениеt-статистики превышает табличное, то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции 
, а, следовательно, и об отсутствии гетероскедастичности.
Если в модели регрессии больше чем одна объясняющая переменная, то проверка гипотезы может осуществляться с помощью t-статистики для каждой из них отдельно.
Тест Голдфелда-Квандта
Самым популярным тестом обнаружения гетероскедастичности является тест, предложенный С. Голдфелдом и Р. Квандтом.
В данном случае также предполагается, что стандартное отклонение 
пропорционально значению xi переменнойXв этом наблюдении, т, е.
Предполагается, что 
имеет нормальное распределение и отсутствует автокорреляция остатков.
Тест Голдфелда-Квандта состоит в следующем:
1. Все п наблюдений упорядочиваются по величинеX.
2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k, (п -2k),kсоответственно.
3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений 
) будет существенно меньше дисперсии регрессии по третьей подвыборке(суммы квадратов отклонений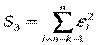 
).
4 Для сравнения соответствующих дисперсий строится следующая F-статистика:
При сделанных предположениях относительно случайных отклонений, построенная F-статистика имеет распределение Фишера с числами степеней свободыv1=v2=k-m-l.
Если
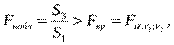
то гипотеза об отсутствии гетероскедастичности отклоняется (
- выбранный уровень значимости).
Тест Уайта (White test, 1980).
Если в модели присутствует гетероскедастичность, то очень часто это связано с тем, что дисперсии ошибок некоторым образом зависят от регрессоров, а гетероскедастичность отражается в остатках обычной регрессии исходной модели.
Проводится этот тест следующим образом:
1) допустим, исходная модель имеет вид:
МНК оцениваются ее параметры и получают регрессионные остатки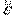 
;
2) оценивается вспомогательная регрессия квадратов остатков на все регрессоры, их квадраты, попарные произведения и константу:
где 
- нормально распределенная ошибка, независимая от εi.
Напомним, что 
. Однако поскольку предполагается, что M(ε) = 0, то D(εi) = M(
). Так как нам неизвестна истинная величина квадратов остатков , то вопрос о наличии гетероскедастичности решается на основе их выборочных аналогов, 
.
Вспомогательная регрессия имеет именно такую форму, потому что необходимо исследовать, существует ли систематическая зависимость между изменениями и какой-либо релевантной переменной модели (чтобы увидеть, что релевантными являются именно переменные, включенные во вспомогательную регрессию, следует представить ошибку в виде 
и возвести данное выражение в квадрат).
3) Проверяется нулевая гипотеза:
Н0: 
и 
и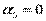 
и 
и 
.
с помощью F– критерия Фишера.
Если фактические значения статистики превышают критические величины распределения Fрасч >Fкр(α,v1=p,v2=n-p-1) то нулевая гипотеза о гомоскедастичности остатков отвергается, то есть делается вывод о присутствии гетероскедастичности.
