Для оценки параметров уравнения множ регрессии, так же как и для оценки этих параметров в простейшем случае парной однофакторной регрессии, используетс МНК. Соотв система норм уравнений имеет структуры имеет структуру, аналогично той, которая была в модели однофакторной регр, но теперь является более громоздкой и для решения можно применить метод определителя.
Уравнение множественной линейной регрессии в матричной форме имеет вид: Y=XB+E
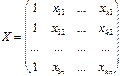
Вопрос № 21 – «Коэффициенты эластичности, их экономический смысл»
В эконометрическом анализе используется эластичность ф-ции, которая рассматривается как отношение изменения У относительно изменения Х.
Э = d Y/Y / d X/X = x/y * f´(x)
Где f´(x) – первая производная, характеризующая соотношение приростов результата и фактора для соответсвия форм связей.
Эластичность показывает, на сколько процентов изменяется функция у=f(х) при изменении независимой переменной х на 1%.
Для линейной: у = а + bх эластичность вычисляется по формуле (4.4.) будет иметь вид:
Т.к. эластичность линейной функции не является постоянной величиной, а зависит от х, то обычно рассчитывают средний показатель эластичности:
Для показательной: у=а*bх
Вопрос № 22 - «Частный и общий F-критерий в оценке результатов множественной регрессии»
Значимость ур-я множественной регрессии в целом оценивается с помощью F-критерия Фишера:
 |
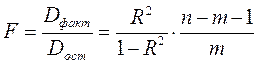(1)
где - факторная сумма квадратов на одну степень свободы;
- коэффициент (индекс) множественной детерминации;
n - число наблюдений;
m - число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов);
- остаточная сумма квадратов на одну степень свободы.
Оценивается значимость не только ур-ия, но и фактора включенного в регрессионную модель
Необходимость такой оценки связана с тем, что не каждый фактор выделяющийся в модели может существенно увеличивать долю объема вариаций результативного признака.
Мерой для оценки включения фактора в модель служит частный F-критерий (
). Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием основного включенного фактора с остаточной дисперсией на общую степень свободы по множественной модели в целом.
Предположим, что оценив значимость влияния фактора х1 как основного включенного в модель фактора, имеющий формулу:
(2) где - коэффициент множественной детерминации для модели с полным набором факторов;
 |
- тот же показатель, но без включения в модель фактора.
Если оценивается значимость влияния фактора Хр после включения в модель факторов Х1, Х2 и т.д. то формула частного F-критерия имеет вид:
(3)
 |
(4)
