В парном регрессионном анализе мы пытаемся объяснить поведение Y путем определения регресс. Зависимости Y от фактора X
Замечание В матем. статистике диспр. анализ рассматривается как самостоятельный метод стат. анализа. Мы его будем применять как вспомогательное средство для изучения кач-ва регрессионной модели
Согласно основной идее дисп. анализа общую сумму квадратов отклонений(я) переменной Y от среднего значения Y можно разложить на 2 части 1)Объясняемую 2) Необъясняемую
1)
 |
-общая сумма откл-й TSS
 |
-обьясненная(регрессионная) сумма кв-тов ESS
 |
-необьясненная(остаточная) сумма квадратов RSS
Общая ∑ квадратов отклонений значений результир. показателя (y1) от среднего значения (y) вызвано множеством причин. Условно разложим всю совокупность на 2 группы: 1)влияние изучаемого фактора X 2) влияние прочих факторов
Если фактор X не влияет на Y то линия регрессии Ox//(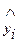
= 
), тогда вся дисперсия результир. показателя обусловлена воздействием прочих факторов: TSS=RSS
Если же прочие факторы не влияют на результат, то Y связан с X функционально и остаточная сумма отклонений отсутствует: TSS=ESS
Пригодность линии регрессии для прогноза зависит от того, какая часть общего отклонения Y приходится на объясненную часть, если ESS> RSS, то уравнение регрессии явл. СТАТ. ЗНАЧИМЫМ и фактор X оказывает существенное влияние на результативный показатель Y.
Любая сумма квадратов отклонений связанна с числом степеней свободы.Число степеней свободы f зависит от объема выборки n и от определенных в этой выборке параметров k.
Для линейной модели k=2, т.к. y=a+bx
Можно показать, что для общей TSS число степеней свободы f1=n-1, для объяснимой ESS f2=k-1, для необъяснимой f3=n-k. k-число параметров
TSS=ESS+RSS (4.1) (n-1)=(k-1)(n-k)
Разделив почл-о каждое слагаемое равенства (4.1) на соответс. степень свободы получим средний квадрат отклонений или дисперсию на 1 степень свободы
S2TSS= 
S2ESS= 
S2RSS= 
или S2= 
(для лин. регр. модели)
Определение дисперсии
На 1 степень свободы приводит их к сравнимому виду и это используется в дальнейшем для проверки ЗНАЧИМОСТИ ФАКТОРА X НА РЕЗУЛЬТИРУЮЩИЙ П-ЛЬ.
Для этого определяют
Замеч-е: в эконометр. исследованиях проверку осущ. при 5% и 1% уровне значимости,
Если H0 отклоняется при 1% уровне значимости, то она автомат. отклоняется и при 5%
Если H0 принимается при 5% уровне значимости, то она автомат. приминется и при 1%
Если при 5% уровне гипотеза отклоняется а при 1% уровне принимается, то результаты проверки проводятся про обоих уровнях значимости
15. Нелинейная регрессия. Подбор линеаризующего преобразования.
Если между экономическими явлениями существуют нелинейные соотношений, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы параболы второй степени
Различают два класса нелинейных регрессий:
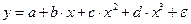1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
Примеры: полиномы разных степеней:
равносторонней гиперболы
2) регрессии, нелинейные по оцениваемым параметрам.
Примеры: степенная
показательная
экспоненциальная
Для первой группы функций
1. 
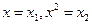В параболе второй степени
заменив
получим двухфакторное уравнение линейной регрессии:
для оценки параметров которого используется МНК.
2. Нелинейность переменной устраняется путем замены переменной.
 |
Вторую группу функций можно разбить на нелинейные модели:
Внутренне линейные
- внутренне нелинейные.
Нелинейность по параметру для внутренне линейных функций часто устраняется путем логарифмирования уравнения.
А) степенная функция (4.3)
Б) показательная функция: (4.4)
В эконометрике степенная функция (4.3.) применяется при моделировании кривых спроса, показательная функция (4.4.) - при моделировании временных трендов.
Если в модели (4.3.) заменить действие, то модель
становится внутренне нелинейной, так её невозможно преобразовать в линейный вид. В этом случае используются итеративные методы, успешность которых зависит от вида функции и особенности самих методов.
16. Корреляция для нелинейной регрессии.
Уравнение нелинейной регрессии также как и в линейной зависимости дополняется показателями корреляции, называемым индексом корреляции.
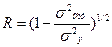Индекс корреляции (R):
 |  | ||
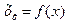где - остаточная дисперсия, определяемая из уравнения регрессии
- общая дисперсия результативного признака y.
 | |||
 | |||
Величина данного показателя находится в границах:
чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
