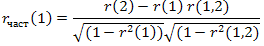Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени.
Рассмотрим два ряда y1, y2,…, yn и y1+τ, y2+τ,…, yn+τ. Эти ряды называются сдвинутыми относительно друг друга на τ единиц или с лагом τ.
Временной ряд yt (t=1, 2,…, n) называется строго стационарным, если совместное распределение вероятностей n наблюдений y1, y2,…, yn такое же, как и n наблюдений y1+ τ, y2+ τ,…, yn+ τ при любых n, t, τ.
Таким образом, свойство строго стационарных рядов не зависят от момента времени t, т. е. в таких рядах от момента времени t не зависит закон распределения и числовые характеристики временного ряда.
Степень тесноты связи между последовательными наблюдениями временного ряда y1,y2,…, yn и y1+τ, y2+τ,…, yn+τ может быть оценена с помощью коэффициента корреляции:
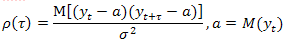
Так как коэффициент ρ(r) измеряет корреляцию членами одного и того же временного ряда, то его называют коэффициентом автокорреляции, а зависимость ρ от r — автокорреляционной зависимостью.
В силу стационарности временного ряда yt автокорреляционная функция ρ(t) зависит только от лага τ и является четной функцией. Таким образом, при изучении автокорреляционной функции можно ограничится только положительным сдвигом τ.
Статистической оценкой ρ является выборочный коэффициент автокорреляции, определяемый по формуле:

Функцию r(τ) называют выборочной автокорреляционной функцией, а её график — коррелограммой.
При расчете r(τ) следует помнить, что с увеличением τ число n-τ пар наблюдений в значении случайной величины уменьшается, поэтому лаг τ должен быть таким, чтобы n-τ было достаточно для вычисления r(τ).
Обычно ориентируются на соотношении τ. Для стационарного временного ряда с увеличением лага τ взаимосвязь между членами временных рядов yt и yt+τ ослабевает, и автокорреляционная функция должна убывать по абсолютной величине.
Наряду с автокорреляционной функцией при исследовании стационарных временных рядов рассматривается частная автокорреляционная функция ρчаст(r), где ρчаст — это частный коэффициент корреляции между рядами yt и yt+τ, то есть коэффициент корреляции между yt и yt+τ при устранении влияния промежуточных членов временных рядов.
Статистической оценкой ρчаст является выборочная автокорреляционная функция rчаст (τ), где rчаст — выборочный частный коэффициент корреляции. Выборочный частный коэффициент автокорреляции первого порядка между членами ряда yt и yt+2 (при устранении влияния промежуточного ряда yt+1) может быть вычислен по формуле: