Изучение связи между 2-мя, 3-мя и т.д. связанными между собой признаками носит название множественной регрессии:
Этапы построения моделей множественной регрессии
I. Выбор формы связи (уравнения регрессии): наиболее приемлемым является способ перебора различных уравнений. Этот подход реализуется на ЭВМ с помощью специально разраб. Алгоритма.
II. Обеспечение достаточного объема совокупности для получения несмещенных оценок (точных значений коэффициентов).
Типы моделей:
1)линейная:
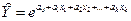2) степенная:
3) показательная:
4) параболическая:
5) гиперболическая:
Отбор факторов, проблема мультиколлинеарности, выбор гипотетической формы уравнения регрессии.
Важным этапом построения уже выбранного уравнения регрессии является отбор и последовательное включение факторных признаков. Сложность формирования уравнения множ. Регрессии в том, что почти все факторы нах. В зависимости др. от др.
Проблема размерности модели (число необходимых факторов) явл. Одной из основных при построении моделей.
Отбор факторных признаков:
Сокращение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации.
В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.
Шаговая регрессия
(шаговый регрессионный анализ)
1). Фактор является незначимым, если его включение в уравнение регрессии только изменяет значение коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения.
2). Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициент регрессии не изменяется (или меняется несущественно), то данный признак существенен и его включение в уравнение регрессии необходимо, он значим.
3). Если же при включении в модель факторного признака коэффициенты регрессии меняют не только величину, но и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак признается нецелесообразным для включения в модель связи (незначим).
Под мультиколлинеарностью понимается тесная зависимость между факторными признаками, включенными в модель.
Наличие мультиколлинеарности между признаками приводит к:
- искажению величины параметров модели, которые имеют тенденцию к завышению;
- изменению смысла экономической интерпретации коэффициентов регрессии;
- осложнению процесса определения наиболее существенных факторных признаков.
Причины возникновения мультиколлинеарности между признаками:
- изучаемые факторные признаки, характеризующие одну и ту же сторону явления или процесса;
- использование в качестве факторных признаков показателей, суммарное значение которых представляет собой постоянную величину;
- факторные признаки, являются составными элементами друг друга;
- факторные признаки, по экономическому смыслу дублируют друг друга.
Этапы решения проблемы мультиколлинеарности:
- - установление наличия мультиколлинеарности;
- - определение причин возникновения мультиколлинеарности;
- - разработка мер по ее устранению.
Одним из индикаторов определения наличия мультиколлинеарности – превышение парных коэф-тов величины 0,8. Необходимо исклюю одну из переменных из модели, при этом какую из переменных оставить, а какую искл. Следует в первую очередь из эк. Соображений.
Если с эк. Точки зрения нельзя отдать предпочтения, то оставляют тот, который имеет больший коэф. Кор-ции. С результатом. В результате число факторов уменьшается в модели и необходимо пересчитать модель и сделать анализ.
Матрица парных коэф-тов корреляции:
| Матрица коэффициентов парной корреляции | |||
| y | x1 | x2 | |
| y | 1,00 | ||
| x1 | 0,95 | 1,00 | |
| x2 | 0,65 | 0,82 | 1,00 |
