Матричні рівняння для мережі взаємозв’язаних гідравлічних елементів аналогічні рівнянням будівельних конструкцій.
Розглянемо гідравлічну мережу, що зображена на рисунку 7.1. У випадку повільних (ламінарних) потоків потік Q через поперечний переріз
труби пропорційний різниці тисків на початку і в кінці труби, Зауважимо, що потік буде ламінарний, якщо число Рейнольдса Re = ρvd / μ не перевищує 2000 (ρ – густина рідини, v – середня швидкість в погодженій системі координат, d – діаметр труби, μ – динамічна в’язкість).
Для елемента е 6 (рис. 7.2) потоки в цю трубу у вузлах 2 і 3 будуть (7.1) і (7.2), відповідно:


Рисунок 7.1
де p 2і р 3 – тиски в вузлах 2 і 3, Q 2 i Q 3витрати потоків в тих же вузлах, а с – стала, яка залежить від властивостей рідини, діаметра і довжини труби.
 |
Рисунок 7.2
В матричній формі рівняння (7.1) набуде вигляду:
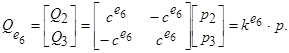 (7.3)
(7.3)
Припустимо, що рідина надходить до мережі в вузлах 1, 2,..., 8 з витратами R 1, R 2,..., R 8, відповідно.
Рівняння нерозривності для вузла 2 має вигляд:
 (7.4)
(7.4)
Система рівнянь типу (7.4) може бути записана таким чином:
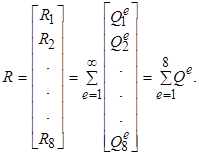 (7.5)
(7.5)
З врахуванням (7.3) формула (7.5) запишеться у вигляді:
R = kР. (7.6)
Порівнюючи формулу (5.2.3.) узагальненого закону Гука для стержневих систем з формулою (7.6), отримуємо їх ідентичність.
Для заданих потоків, що підводяться, вузлові тиски можуть бути знайдені за допомогою рівняння (7.6). Після цього витрати через кожну трубу можна обчислити за допомогою рівняння (7.3).
Будемо розглядати гідравлічні системи, які складаються із трубопроводів, по яких тече рідина та газ або сипучі речовини.
Типова гідравлічна система зображена на рисунку 7.3. Із вузла 1 під тиском рухається рідина в кількості Q 1.
Цю рідину отримують споживачі в кількості Q 5 та Q 3. Система складається із 6 трубопроводів та вузлів: 1, 2, 3, 4, 5 та 6. Наголосимо, що повинні бути задані довжини трубопроводів та їх діаметр. Для системи зображеної на рис. 7.3. відомі такі дані:

Рисунок 7.3
Таблиця 7.1
| Об’єм рідини, см3/с | Довжина труби, м | Діаметр труби, см |
| Q 1 Q 2 Q 3 Q 4 Q 5 Q 6 | L 1=1000 L 2=700 L 3=800 L 4=800 L 5=700 L 6=800 | D =3,07 D =2,81 D =2,21 D =2,91 D =3,34 D =2,91 |
Оскільки між електричним струмом та рухом рідини є певна аналогія, то кажуть, що для вузлів гідравлічної системи справедливий перший закон Кірхгофа: алгебраїчна сума об’ємів рідин, що протікає через вузол, дорівнює нулеві.
Тепер розглянемо контури гідравлічної системи. Для контурів теж виконується закон Кірхгофа, тільки замість напруг розглядають перепади тисків. Розглянемо це питання детально. Для кожної труби справедлива формула Хазена-Паузейля [26]:
D р = KijQ, (7.7)
яка стверджує, що перепад тиску D p пропорційний кількості рідини Q, що протікає через цю трубу. Для коефіцієнта Kij існує [26] така залежність:
 . (7.8)
. (7.8)
Зауважимо, що Ls – довжина труби, по якій протікає рідина Q; ds – діаметр труби; m – динамічна в’язкість рідини чи газу. Так для води m =1,1×10-8 кг×сек/см2.
Цілком зрозуміло, що у формулі (7.8) Ls має розмірність в сантиметрах. Це ж стосується і діаметра труби ds. Для гідравлічної системи, зображеної на рис. 7.3 маємо:
 ;
;
 ;
;
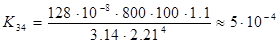 ;
;
 ;
;
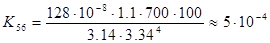 ;
;
 .
.
Зауважимо, що L 1 – основний трубопровід, звідки під тиском р = 2 атм» 2 кГ/см2 йде рух рідини. Користувачі отримують Q 3 та Q 5 рідини. Очевидно, що Qі вимірюється в см3/сек. Вузли 3 та 5 мають атмосферний тиск, тобто ратм » 1 кГ/см2.
Формуємо матрицю інцидентності для вузлів на основі першого закону Кірхгофа:
 .
.
Отримали першу систему:
 . (7.9)
. (7.9)
Згідно з рис. 7.3 маємо 4 контури, для яких обчислюємо за законом Хазена-Паузеля перепади тиску:
Перепади тиску

Отримаємо другу систему рівнянь:
 . (7.10)
. (7.10)
Цілком зрозуміло, що за формулою (7.10) маємо:
D Рij = Kij×Qs. (7.11)
Так, наприклад, для трубопроводу L 1 маємо:
D Р 12= K 12× Q 1. (7.12)
Значення коефіцієнтів Kij вносимо в матрицю інцидентності системи (7.10).
Отримаємо:
 . (7.13)
. (7.13)
Із системи (7.10) беремо два рівняння, а із системи (7.13) беремо три рівняння. Отримали математичну модель гідравлічної системи, зображеної на рис. 7.3.
 . (7.14)
. (7.14)
Наголосимо, що Q 1=1000 см3/сек. Отже, система (3.1.8) містить п’ять рівнянь та п’ять невідомих. Розв’язуємо систему (3.1.8) за методом Гауса і отримаємо:
Q 1=400 см3/c;
Q 3=200 см3/c;
Q 4=200 см3/c;
Q 5=800 см3/c;
Q 6=600 см3/c.
Тепер за формулою (7.11) обчислимо перепади тисків:
D Р 12=5×10-4×103=0,5;
D Р 23=5×10-4×400=0,2;
D Р 34=5×10-4×200=0,3;
D Р 35=5×10-4×200=0,1;
D Р 56=5×10-4×800=0,2;
D Р 25=5×10-4×600=0,3.
Виконаємо перевірку системи (7.9):

Виконуємо перевірку системи (7.10):

Отже ми отримали правильні розв’язки.




