Будемо розглядати матриці розмірністю 3х3 і 4х4.
Матриця dim 3x3:
.
Тоді дане рівняння для даної матриці являє собою визначник третього порядку, який прирівнюємо до нуля:
. (2.3)
Обчислюємо цей визначник і отримаємо:
. (2.4)
Пояснення: tr A = a 11 + a 22 + a 33 – слід матриці А.
S = A 11 + A 22 + A 33. (2.5)
S – сума діагональних алгебраїчних доповнень,
det A – визначник матриці А.
Із курсу вищої математики відомо, що для симетричної матриці А характеристичне рівняння має три дійсних і різних корені. Ці корені називають власними значеннями матриці А.
Матриця dim 4x4:
.
Далі для даної матриці характеристичне рівняння має вигляд:
,
або 
,
де 
;
;
Приклад 1. Обчислити власні значення матриці А:
. (2.6)
Обчислюємо: tr A = a 11 + a 22 + a 33 = 1 + 5 + 1 = 7.
; 
; 
.
|
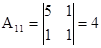S = A 11 + A 22 + A 33 = 4 – 8 + 4 = 0.
det A = a 11× A 11 + a 12× A 12 + a 13× A 13.
Маємо:
;
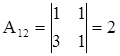
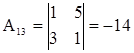det A = 1×4 + 1×3 + 3×(–14)=36.
.
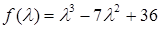. Тоді:
;
.
Прирівняємо першу похідну до нуля:
.
; l 1=0 – точка максимуму;
.
Отже, 
– точка мінімуму.
.
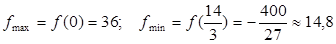Графік функції 
виглядає так:
Рисунок 2.1
З цього графіка робимо висновок, що f (l) має три дійсних корені, причому має таку оцінку: 0 < l 2 < l 3 <=> 0 < l 2 < 14/3, λ 1 < 0.
Ясно, що f (3) = 27 – 7×9 + 36 = 0
Отже, l 2=3. Тоді за теоремою Безу f (x) ділиться на двочлен l -3.
Розв’язуємо квадратне рівняння:
l 2 - 4 l - 12 => l 1= –2; l 3 = 6.
Відповідь. Матриця А має три власні значення: l 1= –2; l 2 = 3; l 3 = 6.
Приклад 2. Обчислити власні значення матриці А.
.
Обчислюємо:
tr A = 1 + 2 + 3 + 4 = 10;
S = 0 + 3 + 4 + 1 - 10 - 6 = -8;
P = 0 - 16 + 4 - 6 = -18;
det A = 7.
Характеристичне рівняння має вигляд:
Нехай 
Тоді
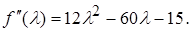
Прирівняємо першу похідну до нуля:
Використовуючи аналогічну методику, яку застосовували в прикладі 1, знаходимо корені квадратичного рівняння:
λ 1 = 10,58, λ 2 = -1,47, λ 3 = -0,35, λ 4 = 1,24.
Означення: Вектор Х (m; n; p) називається власним вектором матриці А, якщо справедлива рівність:
АХ = lХ. (2.7)
Без доведення запишемо робочу формулу для знаходження проекції m; n; та p.
. (2.8)
Підставляючи в систему (2.8) l 1, l 2, знайдемо проекції трьох власних векторів. Запишемо форму для знаходження розв’язків системи (2.8).
. (2.9)
У формулі (2.9) t 
R.
Для матриці А (2.6) ми отримали три власні значення l 1 = –2; l 2 = 3; l 3 = 6.
Обчислимо власні вектори цієї матриці:
а) для l 1 = –2 за формулами (2.9) маємо
.
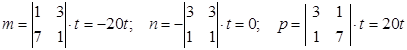Виберемо t =1/20, тоді отримаємо 
.
б) для l 2 = 3 маємо аналогічно 
.
в) для l 3 = 6 маємо 
.
Легко переконатись, що 
; 
; 
.
Без доведення приймаємо такий факт: власні вектори симетричної матриці взаємно перпендикулярні. Сформулюємо матрицю V, стовпцями якої є проекції власних векторів:
. (2.10)
Розглянемо систему трьох лінійних диференціальних рівнянь:
. (2.11)
Без доведення запишемо розв’язок цієї системи:
. (2.12)
Сі (
) – довільні константи.
Зауважимо, що li в формулі (2.12) є власним значенням матриці А для формули (2.11).
Приклад. Знайти розв’язок системи диференціальних рівнянь:
.
Розв’язування
Для матриці А формуємо характеристичне рівняння, яке має вигляд:
l 3 – 9 l 2 + 23 l – 15 = 0.
Обчислюємо три власні значення матриці А:
l 1 = 1; l 2 = 3; l = 5.
Власні вектори мають такі значення:
;
;
.
Тоді матриця V прийме такий вигляд:
. (2.13)
За формулою (2.12) маємо:
.
На основі даного прикладу наведемо ще один важливий фактор. Знаючи матрицю V (2.13), методом “приклеювання” обчислимо обернену матрицю V -1.
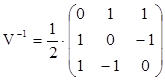. (2.14)
Тепер обчислимо такий добуток: V -1× AV.
Отримали так звану діагональну матрицю, яка складається з нулів, а на головній діагоналі стоять власні значення матриці А.
Без доведення запишемо таку важливу формулу (2.15):
. (2.15)
Якщо нам відома матриця V, що формувалася із проекцій власних векторів матриці А, то формула (2.15) дає можливість обчислити діаго-нальну матрицю D.
Для прогнозування знаків коренів характеристичного рівняння (2.4) без їх обчислення розглянемо питання про його належність до полінома Гурвіца.
2.4 Критерій від’ємності дійсних частин коренів полінома Р (λ)
Для того, щоб стандартний поліном був поліномом Гурвіца, необхідно і достатньо, щоб всі головні діагональні мінори матриці Гурвіца були додатними, тобто
.
Нехай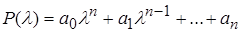 
– деякий характеристичний многочлен.
Тоді матриця розмірністю n´ n:
(2.16)
називається матрицею Гурвіца.
Матриця будується таким чином: по головній діагоналі відкладаються коефіцієнти а 1,..., аn. Вправо по рядку від цих елементів розміщені коефіцієнти зі зменшенням номерів, вліво зі збільшенням.
Головні діагональні мінори цієї матриці будуть мати вигляд:
Приклад 1. Визначити умови від'ємності дійсної частини коренів характеристичного полінома другого степеня.
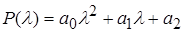, аi> 0 (
).
Матриця Гурвіца в цьому випадку буде мати вигляд:
.
Її головні діагональні мінори: ∆ = а 1, ∆ = а 1 а 2. Таким чином, додатність коефіцієнтів рівняння а 1 > 0, а 2 > 0 є необхідною і достатньою умовою, щоб характеристичний поліном був поліномом Гурвіца.
Приклад 2. Дослідити стійкість розв'язків лінійної однорідної системи диференціальних однорідних рівнянь з постійними коефіцієнтами:
Характеристичне рівняння цієї системи:
або λ 3 + 3 λ 2 + 3 λ + (1 – α 2 β) = 0.
Матриця Гурвіца має вигляд:
Визначники Гурвіца:
∆1 = 3 > 0, ∆2 = 9 – (1 – α 2 β), ∆3 = ∆2(1 – α 2 β).
Таким чином, для додатності головних діагональних мінорів матриці Гурвіца необхідно, щоб параметр β задовольняв нерівності:
.
Метод градієнтного спуску
Загальна задача нелінійного програмування без обмежень полягає в мінімізації f (x) = f (x 1, х 2,..., хn) заданій в n -вимірному евклідовому просторі. Функція f (x) називається цільовою функцією.
Градієнт функції в деякій точці х ( k ) направлений в сторону найшвидшого локального зростання функції. Отже, напрямок, протилежний градієнтному, вкаже шлях, який веде вниз вздовж найбільш крутої лінії. Вектор, протилежний градієнту, називається антиградієнтом.
Ідея методу градієнтного спуску полягає в такому. Вибираємо деяку початкову точку і обчислюємо в ній градієнт функції f (x). Робимо крок в напрямку, протилежному градієнтному:
. (3.1)
Тобто на кожному кроці розв'язується одновимірна задача оптимізації. В результаті приходимо в точку, значення функції в якій менше попереднього. Якщо ця умова не виконується, то необхідно зменшити значення αk. В новій точці процедуру повторюємо: обчислюємо градієнт і знову робимо крок в зворотному до нього напрямку. Процес продовжується до отримання найменшого значення цільової функції. Момент закінчення пошуку наступить тоді, коли рух з отриманої точки з будь-яким кроком приводить до зростання цільової функції. Якщо мінімум функції досягається всередині розглянутої області, то в цій точці градієнт дорівнює нулю, що також може служити сигналом про закінчення процесу оптимізації.
В описаному методі необхідно розраховувати на кожному кроці оптимізації градієнт цільової функції f (х 1, х 2,..., хn):
де 
– частинна похідна від функції f за змінною хk.
Формули для частинних похідних можна отримати в явному вигляді лише в тому випадку, коли цільова функція задана аналітично. В іншому випадку похідні розраховуються за допомогою чисельного диференцію-вання:
де 
, ∆ xk – крок (різниця між сусідніми значеннями аргументу), його приймають 0,001 або 0,005.
Значення градієнта функції f визначаємо за формулою
.
В даній роботі для мінімізації функції використовуємо метод градієнтного спуску з розбиттям кроку. Тобто вибираємо деяке початкове значення х (0). Загальних правил вибору х (0) немає: якщо є інформація про область розміщення шуканої точки х (0), то вибираємо деяке αk = α = const<1 і на кожному кроці процесу (4.1) перевіряємо умову монотонності f (x (k +1)) < f (x (k)). Якщо ця умова порушується, то α розбиваємо до тих пір, поки монотонність не відновиться. Умовою для завершення розрахунку є наступне:
або 
,
де ε – наперед задане мале число (0,0001; 0,000001 і под.), тоді 
. Така умова є необхідною, але недостатньою умовою екстремуму функції в точці x ( k +1). Зауважимо, що точок екстремуму може бути декілька, тому необхідні додаткові дослідження для уточнення яка з точок дійсно являється оптимальною.
Порядок виконання роботи мовою BASIC.
1. Скласти головну програму, яка містить підпрограми: обчислення градієнта функції f -GR та його складових V (І), обчислення цільової функції F.
2. Провести обчислення на ПЕОМ і роздрукувати результати.
Примітка. Значення коефіцієнта αk можна визначити по-іншому. Для цього вводиться одиничний вектор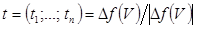 
,
де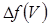 
– загальний вигляд градієнта функції в точці V,
– довжина вектора градієнта.
Після цього вибирається початкова точка 
і визначається координати одиничного вектора 
. Координати нової точки 
при русі по напрямку вектора t (для максимуму функції) 
, або в зворотному напрямку (для мінімуму функції) 
, де а- числовий коефіцієнт.
Підставляємо нові координати у вираз функції, маємо 
. Знаходимо екстремум функції за коефіцієнтом а: 
, звідки і визначаємо а (крок зміни координат). В результаті отримуємо координати нової точки 
. Знаходимо в цій точці значення функції і градієнт 
.
Знову повторюємо процедуру до тих пір, коли значення функції буде не змінюватися і оцінка градієнта буде дорівнювати 0.
Приклад. Мінімізувати функцію 
. За початкове наближення х (0) виберемо точку (0,0) і покладемо ε = 0,0001.
Складемо програму, яка реалізує розв'язування задачі.
Вхідні параметри: N =2 розмірність простору, в якому задана функція f; AL – початкове значення параметра α; х – масив, в елементах якого розміщені значення координат початкової точки x (0); У – значення цільової функції f; E – значення величини ε, що характеризує критерій закінчення ітераційного процесу. Вихідні параметри: k – кількість ітерацій; F – значення функції f; GR – значення градієнта.
ТЕКСТ ПРОГРАМИ
5 INPUT N,AL, EL, E
10 DIM X(N),V(N)
20 DEF FNA (X(1),X(2)) = EXP(C*x(l)^2 +D*х(2)^2)+A*х(1)+B*х(2))
25 FOR I=1 T ON
30 INPUT X(l)
40 PRINT "Х("I") = "; X(I)
50 NEXT I
60 GOSUB 210
65 K = 0
70 GOSUB 220
80 IF GR<E GOTO 170
90 К=К+1
100 FOR I = l, ТО N
110 Х(І)=Х(І) – АL*V(I)/׀GR׀
120 NEXT I
125F1=F
130 GOSUB 210
140 IF F<F1 GOTO 70
145 F=F1
150 AL=0.5*AL
160 GOTO 90
165 PRINT "ТОЧКА MIN"
170 FOR I=1, TO N
180 PRINT "Х("Г)-";Х(I)
185 NEXT I
190 PRINT "F="; F; "КІЛЬК.ІТЕРАЦІЙ = "; К; "ГРАДІЄНТ - "; GR
200 END
210 F=FNA(X(1),X(2)
215 RETURN
220 VE = EXP (C*X(1)^2 +D*X(2)^2)
230 V(l)=A+2*C*X(l)*VE
240 V(2)=B+2*D*X(2)*VE
250 GR = SQR(V(1) ^2 + V(2) ^2)
260 RETURN
В результаті розрахунків маємо:
точка MIN. Х(1) = –0,445472, Х(2) = 0,779575.
F= –1,38011, КІЛЬК. ІТЕРАЦІЙ = 17, ГРАДІЄНТ – 0,0008.
Зауважимо, що на першому кроці оптимізації з використанням методики знаходження коефіцієнта αk з урахуванням екстремуму функції за даним коефіцієнтом (
) маємо:
або
.
Розв’язуючи отримане рівняння, наприклад, за методом ітерацій знаходимо: αk = 0,898715.
Тоді, 
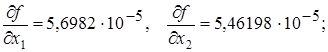
Лінійне програмування
Важливим розділом математичного програмування є лінійне програмування, яке вивчає задачі оптимізації, в яких цільова функція є лінійною функцією проектних параметрів, а обмеження задаються в вигляді лінійних рівнянь і нерівностей.
Канонічна постановка задачі лінійного програмування формулюється так: знайти значення х 1, х 2,…, хn, які:
а) задовольняють систему лінійних рівнянь
. (4.1)
б) є додатними, тобто
х 1≥0, х 2≥0,..., хn ≥0. (4.2)
в) забезпечують найменше значення лінійної цільової функції
. (4.3)
Будь-який розв'язок системи рівнянь (4.1), за умови (4.2), називається допустимим розв'язком. Якщо допустимий розв'язок мінімізує цільову функцію (4.3), то він називається оптимальним розв'язком.
Розглянемо приклад задачі лінійного програмування (транспортну) задачу.
Приклад. Автобаза обслуговує три магазини будівельних матеріалів, причому товари доставляються в магазин з двох складів. Необхідно спланувати перевезення так, щоб їх загальна вартість була мінімальною.
Щоденно вивозиться з першого складу (бази) 12 т товару, з другого 15 т. При цьому завозиться в перший магазин 8 т, в другий – 9 т, в третій – 10 т. Вартість перевезення 1 т товару (в гривнях) з баз в магазин характеризується такою таблицею:
Таблиця 4.1
| База | Магазин | ||
| Перший | Другий | Третій | |
| Перша | 0,8 | 1,1 | 0,9 |
| Друга | 0,7 | 152 |
Розв'язування. Позначимо через х 1, х 2, х 3 кількість товару, який необхідно доставити з першої бази, відповідно, в перший, другий і третій магазини, а через х 4, х 5, х 6 кількість товару, який необхідно доставити з другої бази у вищеподані магазини.
Згідно з умовою задачі маємо:
х 1 + х 2 + х 3 = 12,
х 4 + х 5 + х 6 = 15,
х 1 + х 4 = 8, (4.4)
х 2 + х 5 = 9,
х 3 + х 6 = 10.
Перших два рівняння системи (4.4) описують кількість товару, який необхідно вивезти з першої і другої бази, а три останніх – скільки необхідно завести товару в кожний магазин.
До даної системи необхідно додати систему нерівностей
хi ≥ 0, 
, (4.5)
яка означає, що товар назад з магазинів (крамниць) на бази не вивозиться. Загальну вартість перевезень з врахуванням розцінок запишемо у вигляді
f = 0,8 х 1 + 1,1 х 2 + 0,9 х 3 + х 4 + 0,7 x 5 + 1,2 x 6. (4.6)
Оскільки в (4.4) останнє рівняння є результатом інших, тому ми його відкидаємо. В результаті маємо:
х 1 + х 2 + х 3 = 12,
х 4 + х 5 + х 6 = 15,
х 1 + х 4 = 8, (4.7)
х 2 + х 5 = 9.
Виразимо через х 1 і х 2інші невідомі. Отримаємо:
х 3 = 12 – х 1 – х 2,
х 4 = 8 – х 1,
х 5 = 9 – х 2, (4.8)
х 6 = х 1 + х 2 – 2.
З врахуванням (4.5), отримаємо таку систему нерівностей:
х 1 ≥ 0, x 2 ≥ 0,
12 – х 1 – х 2 ≥ 0,
8 – х 1 ≥ 0, 9 – х 2 ≥ 0, (4.9)
х 1 + х 2 – 2 ≥ 0.
Перепишемо (4.9) в більш компактній формі:
0 ≤ х 1 ≤ 8, 0 ≤ х 2 ≤ 9, 2 ≤ х 1 + х 2 ≤ 12. (4.10)
Цільова функція (4.6) з врахуванням (4.8) виражається через х 1 і х 2:
f = 22,7 + 0,1 х 1 + 0,7 x 2. (4.11)
Враховуючи, що при х 1 і х 2 коефіцієнти додатні, то вартість буде зростати зі збільшенням їх значень. Тому приймаємо з (4.9) х 1 + х 2 = 2. Виключимо один з параметрів, наприклад, х 2. Тоді
f = 24,l – 0,6 x 1. (4.12)
Вартість перевозок буде мінімальною, якщо х 1 = 2, а х 2 = 0.
Оптимальні значення інших проектних параметрів такі: х 3 = 10, х 4 = 6, х 5 = 9, х 6 = 0. В цьому випадку мінімальна загальна вартість перевезень 22,9 грн.
 |
Схема перевезень
Для розв'язання задачі лінійного програмування використовують геометричний метод. Областю розв'язків системи нерівності типу (4.8) є переріз кінцевого числа півплощин, які описуються кожна окремою нерівністю. Перепишемо (4.9) в такому вигляді.
(4.13)
Нерівності (4.13), (4.5) системи обмежень задачі геометрично визначають півплощину відповідно з граничними прямими 
, х 1=0 і х 2=0.
Система (4.13) сумісна, отже область її розв’язків є множина точок, які належать всім даним півплощинам. Оскільки множина точок перетину даних півплощин – випукла, то областю допустимих розв’язків задачі (4.4)-(4.6) є випукла множина, яка називається багатокутником розв’язків (рис. 4.1). Сторони цього багатокутника лежать на прямих, рівняння яких отримуються із системи (4.13) заміною знаків нерівностей на знаки точних рівностей. Таким чином, задача заключається в знаходженні такої точки багатокутника розв’язків, в якій цільова функція f приймає мінімальне значення (аналогічні розсуди і для max значення). Ця точка існує тоді, коли багатокутник розв’язків не пустий і на ньому цільова функція обмежена зверху. При вказаних умовах в одній із вершин багатокутника розв’язків цільова функція приймає мінімальне значення. Для визначення даної вершини побудуємо лінію рівня с 1 х 1+ с 2 х 2= h (де h – деяка стала), яка проходить через багатокутник розв’язків, і будемо її рухати в напрямку вектора 
до тих пір, поки вона не пройде через першу і останню її загальну точку з багатокутником розв’язків. Координати вказаних точок і визначають відповідно мінімальний і максимальний план даної задачі.
Для нашої задачі згідно з (4.11) рівняння лінії рівня таке:
0,1 х 1 + 0,7 х 2 = 1, де h = 1, с1 = 0,1; с2 = 0,7. Вектор 
.
Координати точки А (2; 0) визначають мінімальне значення цільової функції f = 22,7 + 0,1∙2 = 22,9 (грн), тому що при паралельному русі лінія рівня в додатньому напрямку вектора 
перший раз зустрічається з областю допустимих розв’язків (стає опорною лінією) в даній точці.
 |
Рисунок 4.1
Але наведений метод достатньо простий для двох чи навіть трьох змінних.
Одним із методів, за допомогою якого ефективно можна розв'язувати задачі, є симплекс-метод. Ідея симплекс-методу полягає в такому. Приймаємо як початкове наближення координати деякої вершини багатогранника допустимих розв'язків і знайдемо всі ребра, які виходять з цієї вершини. Рухаємося вздовж того ребра, по якому цільова функція спадає. Приходимо в нову вершину, знаходимо всі ребра, які з неї виходять і т.д. В результаті приходимо в таку вершину, рух з якої по будь-якому ребру призводить до зростання цільової функції. Отже, мінімум цільової функції досягнутий в останній вершині з відповідними координатами.
Розглянемо розв'язування задачі (4.1-4.3) симплекс-методом. Якщо в (4.1) задані нерівності, то їх можна перетворити в рівності шляхом введення додаткових невід'ємних змінних, які називають балансовими.
Будемо вважати, що всі рівняння (4.1) лінійно незалежні. В іншому випадку лінійно залежні рівняння відкидаємо.
При m = n система (4.1) має єдиний розв'язок, що виключає деяку оптимізацію.
Виразимо m змінних х 1,..., хm через інші за допомогою рівнянь (4.1):
, 
, pj ≥ 0. (4.14)
Змінні хі називаються базовими, а хm+ 1, хm+ 2,…, хn – вільними змінними.
З врахуванням (4.14) цільову функцію (4.3) перепишемо у вигляді:
f = do + dm+1xm+1 +...+ dnxn. (4.15)
Процес оптимізації починаємо з деякого початкового (опорного) розв'язку, наприклад, при нульових значеннях вільних змінних. Тоді отримаємо:
xі = pi, xm+1 = 0,..., xn = 0. (4.16)
Цільова функція (4.14) прийме значення:
f (0) = d 0.
Перевіряємо на оптимальність розв'язок (4.16). Якщо в (4.15) коефіцієнти dm+ 1 ,…, dn невід'ємні, то при збільшенні вільних змінних цільова функція не може зменшитись. В цьому випадку розв'язок (4.16) є оптимальним.
Тепер нехай серед коефіцієнтів (4.15) є хоч один від'ємний, наприклад, dm+ 1< 0. Тоді, як новий опорний розв'язок вибираємо змінні при таких значеннях параметрів:
xm+ 1 = х (0) m+ 1, xm+ 2 = 0,…, xn = 0. (4.17)
Тоді базисні змінні згідно з (4.14) будуть мати вигляд:
xі = pi + qі,m+1x (1) m+1, 
. (4.18)
Якщо всі коефіцієнти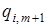 
невід'ємні, то хm+ 1 можна збільшувати необмежено. Тоді не існує оптимального розв'язку задачі. Коли серед коефіцієнтів 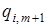є від'ємні, то необхідно контролювати знак х 
при збільшенні змінної xm+ 1. Цю умову можна записати у вигляді:
, . (4.19)
Серед всіх від'ємних коефіцієнтів 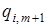вибираємо найбільший за модулем. Нехай його значення дорівнює Q, а відповідне йому значення pі дорівнює Р. Тоді з (4.19) отримаємо максимальне значення (4.17):
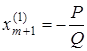(P > 0, Q < 0),
і новий опорний розв'язок запишемо у вигляді:
. (4.20)
Нова цільова функція дорівнює:
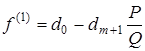. (4.21)
На цьому закінчується перший крок оптимізації. Тепер необхідно зробити наступний крок, використовуючи аналогічну процедуру. Для цього вибираємо новий базис: х 1,..., хm- 1, xm, хm+ 1. Після другого кроку знаходимо нове значення цільової функції f (2). Якщо f (2) <f (1), то ми знаходимо нові оптимальні значення змінних або показуємо, що розв’язок (4.20) не є оптимальним.
В будь-якому випадку після кінцевого числа кроків ми приходимо до оптимального розв'язку.
Розв'яжемо попередню транспортну задачу симплекс-методом. Приймаємо х 3, х 4, х 5, х 6 в якості базисних і виражаємо їх через вільні змінні х 1 і х 2. Тоді маємо систему (4.8).
Як опорний розв'язок візьмемо такі значення, які відповідають нульовим значенням вільних параметрів:
х (0)1 = 0, х (0)2 = 0, х (0)3 = 12, х (0)4 = 8, х (0)5 = 9, х (0)6 = –2.
Маємо протиріччя: х (0)6 < 0.
Нехай х 2, х 4 вільні параметри і х (0)3 = 0, х (0)4 = 0, тоді х (0)1 = 8, х (0)3 = 4, х (0)5 = 9, х (0)6 = 6 і f = 23,5.
Дослідимо отриманий розв'язок з врахуванням вигляду опорного розв'язку і цільової функції через вільні параметри х 2, x 4.
З врахуванням (4.6) і (4.7) маємо:
х 1 = 8 – х 4,
х 3 = 4 – х 2 + х 4,
х 5 = 9 – х 2, (4.22)
х 6 = 6 + х 2 – х 4,
f = 23,5 – 0,1 х 4 + 0,7 х 2. (4.23)
Коефіцієнт при х 4 – від'ємний, а при х 2 додатний. Для мінімуму функції f можна збільшувати значення х 4 при мінімальному значенні х 2. Покладемо х 2 = 0. З системи (4.22) маємо:
х 1 = 8 – х 4,
х 3 = 4 + х 4,
х 5 = 9, (4.24)
х 6 = 6 – х 4.
З системи (4.24) знаходимо, що максимальне значення х 4 буде 6. Тоді цільова функція дорівнює:
f = 23,5 – 0,1·6 = 22,9
і згідно з (4.24) опорні розв'язки будуть мати вигляд:
х 1 = 2, х 2 = 0, х 3 = 10, х 4 = 6, х 5 = 9, х 6 = 0.
Відповідь збіглася з попередньою.
