Наряду с движением вязкой жидкости в круглых цилиндрических трубах были изучены также и переходные движения в пространстве между соосными вращающимися цилиндрами [4]. При переходе через некоторое значение числа Рейнольдса устойчивое вначале круговое движение частиц ньютоновской жидкости в плоскостях, перпендикулярных к оси вращения, сменяется движением с ячеистой структурой замкнутых вторичных течений, расположенной периодически в направлении, параллельном оси вращения. Такое – его обычно называют тейлоровским – движение образуется в случае доминирующего вращения внутреннего цилиндра. В случае же доминирующего значения вращения внешнего цилиндра устойчивое круговое движение частиц переходит в спиральное, смешанное ламинарно – турбулентное движение. Эти периодически расположенные в пространстве спирали, сохраняя свою форму и взаимное расположение, вращаются как одно целое вокруг общей оси цилиндров с угловой скоростью, близкой к среднему арифметическому угловых скоростей цилиндров.
Изменяя угловые скорости вращение внутреннего и внешнего цилиндра, можно отчетливо наблюдать процессы возникновения и разрушения различных режимов движений ньютоновской жидкости между вращающимися цилиндрами, от периодических тейлоровских до двоякопериодических спиральных структур. Теоретически задачу об устойчивости движения ньютоновской жидкости между двумя коаксиальными цилиндрами исследовал Тейлор [2]. Как качественно, так и количественно теория Тейлора дает очень хорошее совпадение с опытом.
Исследование гидродинамической устойчивости течения ньютоновской жидкости между соосными цилиндрами проводилась экспериментально также при помощи цилиндрического вискозиметра, в котором внутренний цилиндр вращался, а наружный был свободно подвижен на упругой проволоке. Появление неустойчивости характеризовалось разрывом величины и наклона кривой течения. Результаты экспериментов хорошо согласовались с теоретическими расчетами, полученными по теории Тейлора [2].
В вязкопластичных жидкостях возникновение неустойчивости основного ламинарного движения, которое затем может привести к образованию турбулентного движения, происходит двумя путями [12]. Первый путь – появление неустойчивости после предельного разрушения структуры в ламинарном течении вязкой жидкости. Второй путь, когда неустойчивым становится основное ламинарное структурное течение вязкопластичной жидкости, то есть неустойчивость течения появляется до предельного разрушения структуры. В этом случае с наступлением неустойчивости основная структура среды разрушается, но сохраняются ее остатки в малых объемах.
Существование обоих путей появления неустойчивости ламинарного течения вязкопластичной жидкости ясно видно на кривых течения, полученных в опытах по исследованию реологических свойств красок. Опыты проводились на ротационном вискозиметре с радиусом внутреннего цилиндра R1 = 3,83 см и наружного R2 = 3,95 см, длина внутреннего вращающегося цилиндра l = 23,5 см. На кривых течения по оси абсцисс отложено напряжение τ = М/2πR21l, а по оси ординат – скорость деформации ε=2πna, где n – число оборотов цилиндра в секунду, «а» константа данного вискозиметра (рис. 6.2, 6.3).

Рис. 6.2.
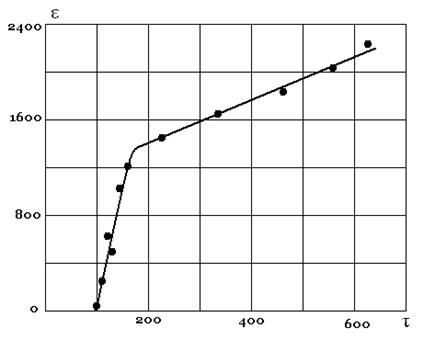
Рис. 6.3.
По кривой течения охры с водой (рис. 6.2) видно, что неустойчивость, характеризуемая изменением наклона кривой течения, появляется в ламинарном течении с предельно разрушенной структурой, то есть в вязкой ньютоновской жидкости (кружками отмечены экспериментальные точки). Для этого случая проведено сравнение данных опыта с теорией устойчивости Тейлора. Отклонение экспериментального значения критического параметра Тейлора Ткр от теоретического значения составляет 6,4%.
Показано, что у сурика с пирофосфатом натрия (рис. 6.3) неустойчивость движения, характеризуемая изменением наклона реологической кривой течения, появляется до предельного разрушения структуры, непосредственно в структурном режиме движения вязкопластичной жидкости. Для подобных сред проведено сравнение опытных данных с теоретическими результатами, полученными в работе [12], которое показало, что максимальное отклонение опытных значений Т¢кр от теоретических составляет 8%.
Интересные исследования были проведены по переходу ламинарного пограничного слоя в турбулентный при обтекании шара потоком воздуха. Эксперименты показали, что при числе Рейнольдса равного приблизительно 3∙105, коэффициент сопротивления шара внезапно уменьшается от 0,5 до 0,15. Столь резкое уменьшение сопротивления объясняется появлением в пограничном слое турбулентного течения. Возникновение в пограничном слое сильного перемешивания значительно усиливает увлекающее действие внешнего потока по сравнению со случаем ламинарного пограничного слоя, и это приводит к перемещению точки отрыва назад, то есть вниз по течению. Если для пограничного слоя остающегося ламинарным на всем протяжении, точка отрыва лежит приблизительно на экваторе шара, то после турбулизации пограничного слоя она перемещается на довольно значительное расстояние назад, то есть на заднюю половину шара. Вследствие этого область застоя течения позади тела значительно суживается, что приводит к значительному уменьшению коэффициента сопротивления. Такое явление получило название кризиса сопротивления.
Кризис сопротивления может осуществляться при числах Рейнольдса значительно меньших критических, если искусственно турбулизовать пограничный слой путем введения в него специального турбулизатора. Л. Прандтль провел следующий опыт. Несколько впереди экватора шара, обтекавшегося потоком воздуха, он укрепил на поверхности шара тонкое проволочное кольцо. Наличие этого кольца вызвало искусственную турбулизацию пограничного слоя, уже при умеренном числе Рейнольдса и повлекло за собой такое же изменение сопротивления, как и увеличение числа Рейнольдса при отсутствии кольца.
Литература
1. Седов Л.И. Механика сплошной среды. Т.2. Л.: Лань, 2004. – 528 с.
2. Ландау Л.Д., Лившиц Е.М. Теоретическая физика. Т.6. Гидродинамика – М.: Наука, 2004. – 736 с.
3. Лойцянский Л.Г. Механика жидкости и газа. – М.: Наука. 1987 – 840 с.
4. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Ч. II. – М.: Физматгиз, 1963. – 727 с.
5. Слезкин Н.А. Динамика вязкой несжимаемой жидкости. – М.: Гостехиздат, 1955. – 519 с.
6. Шлихтинг Г. Теория пограничного слоя. – М.: ИИЛ, 1956. – 528 с.
7. Огибалов П.Н., Мирзаджанзаде А.Х. Нестационарное движение вязкопластичных сред. – М.: МГУ, 1970. – 415 с.
8. Шульман З.П., Берковский Б.М. Пограничный слой неньютоновских жидкостей. – Минск. Наука и техника, 1966. – 238 с.
9. Астрахан И.М. Розенберг Г.Д. Механика неньютоновсих жидкостей. – М.: РГУ нефти и газа им. И.М. Губкина, 1999. – 30 с.
10. Астрахан И.М., Лурье М.В., Юфин А.П. Гидравлика. Ч. I. – М.: МИНХ и ГП им И.М. Губкина, 1974. – 115 с.
11. Монин А.С., Яглом А.М. Статистическая гидромеханика. Ч.1. Раздел «Гидродинамическая неустойчивость и возникновение турбулентности». – М.: Наука, 1965. с. 77 – 161.
12. Астрахан И.М. Устойчивость вращательного движения вязкопластичной жидкости между двумя коаксиальными цилиндрами. Прикладная механика и техническая физика. Изд. АН СССР. 1961. № 2, с. 47 – 53.
13. Белкин И.М., Виноградов Г.В., Леонов А.И. Ротационные приборы. Измерение вязкости и физико-химических характеристик материалов. – М.: Машиностроение, 1968. – 270 с.
14. Бетчов Р., Криминале В. Вопросы гидродинамической устойчивости. – М.: Мир, 1971.
15. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика. – М. – Ижевск, ИКС, 2003. – 480 с.
16. Edwards M.F., Nellist D.A., Wilkinson W.L. Unsteady, laminar flows of non-Newtonian fluids in pipes. Chemical Engineering Science. 1972. vol. 27, pp. 295 – 306.
17. Астрахан И.М. Об уравнениях движения вязкопластичной жидкости в пограничном слое на произвольной поверхности. Известия АН СССР, ОТН, Механика и машиностроение. 1960. №2, с. 54 – 59.
Оглавление
| Предисловие …………………………………………………………...... | |
| Глава I. Реологические уравнения ньютоновской и неньютоновских вязких несжимаемых жидкостей ………………………………... | |
| §1.Реология – учение о течении сплошных сред ………………… | |
| §2.Классификация неньютоновских жидкостей …………………. | |
| §3.Неньютоновские вязкие жидкости ……………………………. | |
| §4.Жидкости, реологические характеристики которых зависят от времени ……………………………………………………….. | |
| §5.Вязкоупругие жидкости ………………………………………... | |
| Глава II. Дифференциальные уравнения движения вязких несжимаемых жидкостей ………………………………………… | |
| §1.Уравнения движения в напряжениях …………………………. | |
| §2.Уравнения движения вязкой ньютоновской несжимаемой жидкости (уравнения Навье – Стокса) ………………………… | |
| Глава III. Точные решения уравнений движения вязких (ньютоновских и неньютоновских) жидкостей ……………. | |
| §1.Ламинарное прямолинейное установившееся движение вязких жидкостей в круглых трубах …………………………… | |
| §2.Коэффициент гидравлического сопротивления при течении в трубах ……………………………………………………………. | |
| §3.Вращательное движение жидкости в кольцевом зазоре ……... | |
| §4.Вискозиметрические методы определения реологических параметров жидкостей ………………………………………….. | |
| §5.Пульсирующее ламинарное движение вязкой ньютоновской жидкости в круглой цилиндрической трубе …………………... | |
| Глава IV. Движение вязкой жидкости при малых числах Рейнольдса... | |
| §1. Уравнения движения ньютоновской жидкости при малых числах Рейнольдса ………………………………………………. | |
| §2.Пространственное движение вязкой несжимаемой жидкости между двумя безграничными параллельными плоскостями. Закон Дарси ……………………………………………………… | |
| §3.Обтекание шара потоком жидкости …………………………... | |
| §4.Гидродинамическая теория смазки …………………………… | |
| §5.Нестационарное пульсирующее движение неньютоновских степенных жидкостей в трубах ………………………………… | |
| Глава V. Движение вязких жидкостей при больших числах Рейнольдса …………………………………………………………. | |
| §1.Понятие о пограничном слое.Уравнения ламинарного пограничного слоя в ньютоновской жидкости ………………... | |
| §2.Пограничный слой при обтекании несжимаемой жидкостью плоской пластины. Задача Блязиуса …………………………… | |
| §3.Отрыв пограничного слоя ……………………………………… | |
| §4.Приближенные методы расчета ламинарного пограничного слоя. Интегральное соотношение Кармана …………………… | |
| §5.Задача о плоской ламинарной затопленной струе …………… | |
| §6.Пограничный слой в вязкопластичных жидкостях …………... | |
| Глава VI. Неустойчивость ламинарных режимов течений и возникновение турбулентности в вязких ньютоновских и неньютоновских жидкостях ……………………………………... | |
| §1.Исследования устойчивости ламинарных течений …………... | |
| §2.Устойчивость вращательного течения ньютоновских и вязкопластичных жидкостей между двумя цилиндрами ……... | |
| Литература …………………………………………………………. |






