Рассмотрим теперь задачу о плоском установившемся движении вязкой жидкости в виде струи, исходящей из узкого отверстия 
. Пусть в покоящейся жидкости, расположенной справа от оси Оу, распространяется струя жидкости, исходящая из очень узкого отверстия, находящегося в начале координат, и имеющая ось Ох осью симметрии (рис. 5.4). Вследствие трения струя захватывает некоторую часть покоящейся жидкости и увлекает ее за собой. Струя расширяется вниз по течению, в то время как скорость течения в центре струи уменьшается. Принимаем, что щель бесконечно узка, поэтому для того, чтобы количество протекающей жидкости, а также импульс имели конечные значения, скорость в щели должна быть бесконечно большой. Так как поперечные размеры струи весьма малы по сравнению с продольными, то мы можем применить уравнения теории пограничного слоя. Конечно, как и в случае пластинки, полученные результаты будут пригодны только начиная с некоторого удаления от начала координат.
В виду того, что в покоящейся жидкости мы имеем постоянное давление и, следовательно, отсутствие градиента давления, то для функции тока ψ (х,у) мы получаем то же уравнение
, (5.62)
как и в случае обтекания пластинки равномерным потоком. Однако граничные условия будут теперь другими. А именно, на оси Ох мы имеем условия:
, 
при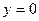 
,(5.63)
вытекающие из симметрии движения относительно оси Ох. Условие на бесконечности в данном случае принимает вид:
при 
(5.64)
так как основной поток отсутствует и, следовательно, 
.
Докажем теперь, что количество движения жидкости, проходящее через каждую прямую х=х о, будет постоянной величиной, не зависящей от х о. В самом деле, через элемент dy прямой х=х о проходит масса жидкости 
, несущая количество движения 
, проекция которого на ось Ох равна 
.Вследствие симметрии, нам достаточно найти проекцию количества движения жидкости на ось Ох; эта проекция имеет величину
. (5.65)
Если жидкость простирается до бесконечности и там находится в покое, то давление можно считать всюду постоянным, то есть р=const. Применяя теорему об изменении количества движения жидкости к области между двумя прямыми, параллельными оси у, и, используя постоянство давления, мы приходим к выводу о постоянстве переносимого струей количества движения, то есть
.
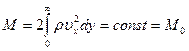Чтобы решить уравнение (5.62), положим
; 
, 
, 
.
Обозначая штрихами производные по ξ, легко найдем, что
, 
,
, 
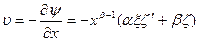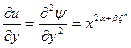, (5.66)
.
Поэтому уравнение (5.62) принимает вид:
. (5.67)
Мы получим обыкновенное дифференциальное уравнение для определения ζ, если примем, что
,
откуда
.
С другой стороны, условие
приводит к равенству
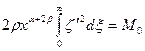(5.68)
и так как М о не зависит от х, то необходимо положить
.
Решая два полученных уравнения для α и β, находим
; 
.
Итак, если мы примем, что
, 
, (5.69)
то для определения ζ(ξ) мы будем иметь вытекающее из (5.67) уравнение
. (5.70)
Из (5.63), (5.64) и (5.66) вытекают граничные условия, которым должна удовлетворять функции ζ(ξ):
при 
,
при 
. (5.71)
Уравнение (5.70) очень легко интегрируется
.
Из условий (5.71) следует, что надо принять С1=0, так что
.
Это уравнение опять-таки интегрируется
.
Так как при , то значение С2 неотрицательно, положим поэтому
.
Итак,
, или 
;
интегрируя это уравнение, находим:
.
Так как 
ζ=0 при ξ=0, то С3=0. Поэтому
, 
.
Для сокращения письма положим:
,
тогда находим окончательный результат
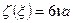
. (5.72)
Величина а легко выражается через М о путем использования формулы (5.68):
;
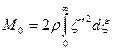но
; 
; 
; 
,
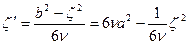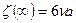поэтому
. (5.73)
Итак,
. (5.74)
Пользуясь выражением (5.72) и (5.69) для ζ(ξ), получаем:
. (5.75)
Для проекций скорости легко находим выражения [4]:
,
. (5.76)
Рисунок (5.4) дает построенные на основе этих выражений линии тока и зависимость составляющей скорости u от у в трех сечениях струи. Из нее ясно видно, как струя постепенно захватывает все большее количество жидкости. Легко проверить это и аналитически. Количество жидкости, протекающей через прямую, параллельную оси Оу и отстоящую от нее на расстоянии х, очевидно, равно
но
,
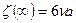и, следовательно,
. (5.78)
Этот процесс связан с подтеканием жидкости к оси Ох, и действительно, легко видеть, что
; 
;
это подтекание наиболее интенсивно в непосредственной близости от оси Оу и убывает по мере возрастания х. Таким образом, расход через начальное сечение струи (х=0) равен нулю, а затем расход растет благодаря подтеканию с боков струи. Расход растет также с увеличением импульса.
