Интегр ур-ние Фредгольма 2-го рода имеет вид: 
. (1)
Здесь 
– заданная функция, кот наз ядром интегр ур-ния; 
- заданная функция, кот наз. свободным членом или правой частью интегp. ур-ния; l - заданное число, наз паpаметpом интегp уp-ния; 
- искомая функция, подлежащая опpеделению. Однородное интегральное уравнение Фредгольма 2-го рода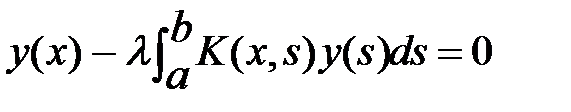 
, (2)
всегда имеет тривиальное решение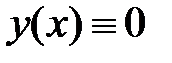 
. Значения параметра 
, при кот однородное ур-ние (2) имеет нетривиальные реш, наз собственными значениями ядра 
, а сами нетривиальные решения – собственными функциями ядра.Для интегр ур-ния Фредгольма 2-го рода возможны две альтернативы: 1)неоднородное интегр ур-ние Фредгольма (1) имеет единственное реш. при любых правых частях; 2)оответствующее однор. ур-ние (2) имеет нетривиальные решения.
Аппроксимация интегрального уравнения системой линейных алгебраических уравнений.
Hа отpезке 
зададим сетку 
и для каждого узла сетки pассмотpим интегpальное уpавнение (1): 
. (3)
В выражении (3) для вычисления интегpала воспользуемся квадpатуpной фоpмулой вида:
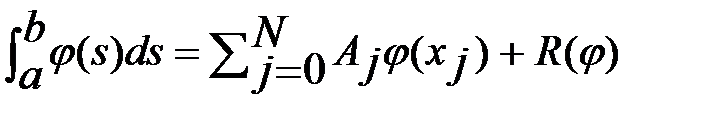(4)
При использовании составной квадратурной формулы средних прямоугольников
.
При использовании составной квадратурной формулы трапеций:
.
При использовании составной квадратурной формулы парабол имеем: 
.
Применение квадратурной формулы приводит к выражению 
, (5) откуда после отбpасывания остаточного члена получаем относительно пpиближенных значений 
pешения 
в узлах 
систему линейных алгебраических уpавнений:
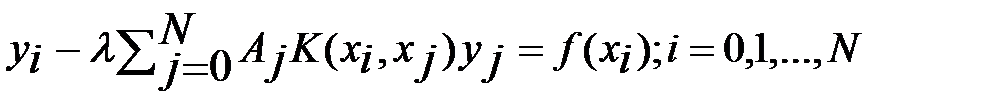. (6)
Как следует из (5) система (6) аппроксимирует интегральное уравнение (1) в узлах сетки с погрешностью 
. Введем в рассмотрение матрицу B с элементами 
Тогда определитель системы (6) можно записать в виде 
. Если 
, то система (6) имеет единственное решение, которое можно записать в форме Крамера 
.
Решение проблемы собственных значений для ядра.
В случае однор интегр ур-ния (2) при решении задачи на собственные значения для ядра получаем указанным способом алгебраическое уравнение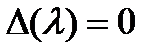 
степени, вообще говоря, 
относительно . Корни 
этого уравнения будут приближенными значениями первых собственных значений ядра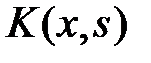 
. Приближения для собственных векторов находятся из системы (6) при 
и соответствующем значении параметра 
.
Оценка погрешности и сходимость метода квадратур
Пусть функция 
непрерывна на 
, ядро 
непрерывно на декартовом произведении 
и числовой параметр 
в интегр ур-нии (1) не является собственным значением ядра. В силу альтернативы Фредгольма, ур-ние (1) имеет единственное решение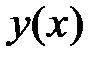 
. В пределе при 
и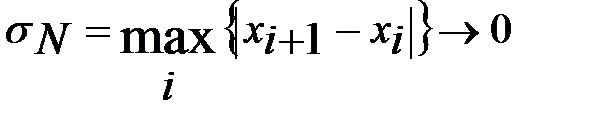 
решение 
системы (6) существует, единственно и сходится к реш интегр ур-ния. Таким образом, при достаточно больших N можно считать, что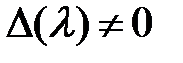 
.
При решении системы (6) имеет место вычислительная погрешность. Поэтому фактически найденные значения 
точно удовлетворяют системе
. (6’)
Погрешность полученного решения в узлах сетки выражается разностью 
. Вычитая ур-ния (6’) из уравнений (5) для погрешности получим систему 
. (7)
Отсюда, используя формулы Крамера
, получаем для погрешности оценку
, где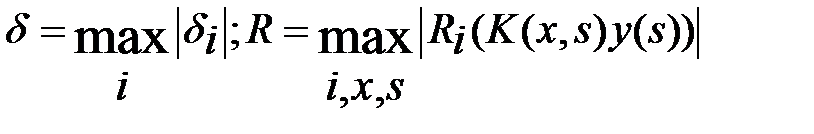 
.
