Комплексное сопротивление равно отношению комплекса напряжения к комплексу тока, или комплексного максимального значения напряжения к комплексному максимальному значению тока. Z=  =
= 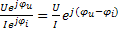 =Z
=Z 
Где:Z- модуль комплексного сопротивления, называется полным сопротивлением, 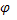 - аргумент комплексного сопротивления, равен углу сдвига фаз между напряжением и током, R- вещественная часть комплексного сопротивления, называется активным сопротивлением, X- мнимая часть комплексного сопротивления, называется реактивным сопротивлением. Графически выражение Z2=R2+X2,
- аргумент комплексного сопротивления, равен углу сдвига фаз между напряжением и током, R- вещественная часть комплексного сопротивления, называется активным сопротивлением, X- мнимая часть комплексного сопротивления, называется реактивным сопротивлением. Графически выражение Z2=R2+X2,  можно представить треугольником сопротивлений. Комплексное сопротивление идеальных двухполюсников: для сопротивления R Z=R(активное), для индуктивности L комплексное сопротивление
можно представить треугольником сопротивлений. Комплексное сопротивление идеальных двухполюсников: для сопротивления R Z=R(активное), для индуктивности L комплексное сопротивление 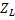 =j
=j  =-j
=-j 
 где
где  - реактивное сопротивление емкостного элемента.
- реактивное сопротивление емкостного элемента.
Комплексная проводимость. величину, обратную комплексному сопротивлению называют комплексной проводимостью: Y= 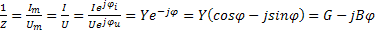 , где:
, где:
Y модуль комплексной проводимости, называется полной проводимостью, G- активная проводимость, В-реактивная проводимость графически данное выражения Y= 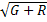 можно представить в виде треугольника проводимости. Комплексная проводимость этих же элементов Y=G,
можно представить в виде треугольника проводимости. Комплексная проводимость этих же элементов Y=G,  =
= 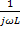 ,
,  . Если известно комплексное сопротивление, то можно найти комплексную проводимость: Z=R+jX Y=
. Если известно комплексное сопротивление, то можно найти комплексную проводимость: Z=R+jX Y=  .
.
Если известно проводимость, то можно получить сопротивление.
Пассивный двухполюсник. Схемы замещения. По известному входному комплексному сопротивлению двухполюсника можно получить последовательного соединения активного сопротивления и реактивного сопротивления. В зависимости от знака реактивного сопротивления и его можно рассматривать как индуктивное или как емкостное.
Напряжения U можно разложить на две составляющие: U=ZI=(R+jX)I=IR+jIX=  где
где  –составляющая совпадающая по фазе с током называется активной составляющей напряжения,
–составляющая совпадающая по фазе с током называется активной составляющей напряжения,  составляющая, сдвинутая по фазе относительно тока на угол
составляющая, сдвинутая по фазе относительно тока на угол  , называется реактивной составляющей напряжения. Составляющие
, называется реактивной составляющей напряжения. Составляющие  ,
,  рассматриваются как напряжения на элементах R и X.
рассматриваются как напряжения на элементах R и X.
Из треугольника напряжений следует U= 
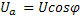
 . Входной проводимости Y=G-jB соответствует параллельная схема замещения из активной проводимости и реактивной проводимости В. Реактивная проводимость в зависимости от знака либо индуктивная, либо емкостная. Ток на входе может быть представлен. I=YU=(G-jB)U=GU-jBU=
. Входной проводимости Y=G-jB соответствует параллельная схема замещения из активной проводимости и реактивной проводимости В. Реактивная проводимость в зависимости от знака либо индуктивная, либо емкостная. Ток на входе может быть представлен. I=YU=(G-jB)U=GU-jBU=  , где
, где 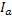 - составляющая, совпадающая по фазе с напряжением, называется активной составляющей тока,
- составляющая, совпадающая по фазе с напряжением, называется активной составляющей тока,  составляющая, сдвинутая по фазе относительно напряжения на угол
составляющая, сдвинутая по фазе относительно напряжения на угол  , называется реактивной составляющей тока. Составляющие
, называется реактивной составляющей тока. Составляющие 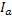 и
и  рассматриваются как токи в элементах G и В. Треугольник образованный I
рассматриваются как токи в элементах G и В. Треугольник образованный I 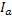
 называется треугольникам токов.
называется треугольникам токов.
Закон Ома и Кирхгофа в комплексной форме. Закон Ома: U=ZI.
Первый закон Кирхгофа: алгебраическая сумма комплексных токов в проводниках, соединенных в узел, равна нулю:  .
.
Второй закон Кирхгофа: алгебраическая сумма комплексных напряжений на всех элементах любого замкнутого контуре равна нулю. Его можно сформулировать другим образом: алгебраическая сумма комплексных напряжений на всех элементах любого замкнутого контура равна алгебраической сумме комплексных э.д.с. всех источников напряжения в этом контуре: 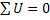
 . Законы Кирхгофа можно записать и для мгновенных значений. Алгебраическая сумма мгновенных значений токов в ветвях, соединенных в узле равна нулю:
. Законы Кирхгофа можно записать и для мгновенных значений. Алгебраическая сумма мгновенных значений токов в ветвях, соединенных в узле равна нулю:  . Алгебраическая сумма мгновенных напряжений на всех элементах любого замкнутого контура схемы равна нулю:
. Алгебраическая сумма мгновенных напряжений на всех элементах любого замкнутого контура схемы равна нулю: 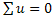 , или алгебраическая сумма мгновенных э.д.с. всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура.
, или алгебраическая сумма мгновенных э.д.с. всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура.
Вопросы для самоконтроля:
1.комплексная, полная, реактивная проводимости
2.Треугольник проводимости.
3. Как перейти от комплексных сопротивлений к комплексным проводимостям и обратно
4. Соотношения межу амплитудами и начальными фазами синусоидального тока и напряжения на резистивном элементе.
5. Чему равен угол сдвига фаз между напряжением и током на резистивном элементе.






