Закон Ома для пассивного участка цепи:
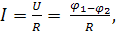где 
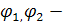потенциалы точек 1 и 2; U- разность потенциалов или напряжение между точками 1 и 2.
Для участка цепи содержащей э.д.с: 
Формулу можно написать дя любого участка сложной электрической цепи с произвольным числом э.д.с., сопротивлений и заданной разностью потенциалов на концах этого участка.
Для одноконтурной замкнутой цепи также применяется закон Ома: 
Для написания законов Кирхгофа необходимо ввести следующие понятия: узел, ветвь, контур. Узел – место соединения, в котором сходятся три и более ветвей. Ветвь – участок электрической цепи, вдоль которого протекает один и тот же ток. Контур – любой замкнутый путь образованный ветвями и узлами.
Первый закон Кирхгофа: алгебраическая сумма токов ветвей, сходящихсяв узле, равна нулю: 
Количество независимых уравнений, составляемых по первому закону Кирхгофа равно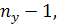 
где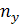 
количество узлов схемы. Второй закон Кирхгофа: алгебраическая сумма напряжений все ветвей в любом контуре равна нулю. С учетом напряжений элементов, можно сформулировать закон Кирхгофа в следующей формулировке: алгебраическая сумма э.д.с. замкнутого контура равна алгебраической сумме падений напряжений на сопротивлениях, входящих в этот контур:
Количество независимых уравнений по второму закону Кирхгофа 
где 
- число ветвей схемы. Пользуясь законом Кирхгофа, можно найти напряжение между любыми точками. Законы Кирхгофа выполняются для любого момента времени.
Потенциальная диаграмма. График распределение потенциала вдоль замкнутого контура называется потенциальной диаграммой.
Эквивалентные преобразования. В основе методов преобразования электрических схем лежит принцип эквивалентности, согласно которому токи и напряжения в ветвях схемы не затронутых преобразованием остаются неизменными.
ْْْ
Последовательное соединение. Т Электрическая цепь из последовательно соединенных сопротивлений. Ток в цепи один; напряжение на входе равно сумме напряжений на элементах. Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных сопротивлений: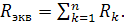 
Напряжение на элементах: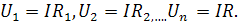 
Параллельное соединение. Рассмотрим цепь из параллельно соединенных элементов сопротивлений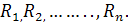 
На всех элементах имеем одно и то же напряжение, ток на входе цепи равен сумме токов элементов:
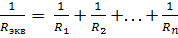где 
эквивалентная проводимость цепи.
Рассмотрим частный случай: параллельное соединение двух сопротивлений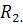 
Ток в неразветвленной части: 
где 
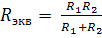– эквивалентное сопротивление цепи.
Смешенное соединение. Это сочетание последовательного и параллельного соединения сопротивлений.
Эквивалентное сопротивление для последовательно- параллельного соединения элементов: 
Ток в неразветвленной части токи в параллельных ветвях определяются формулой разброса:
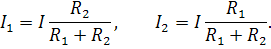
Преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений. Рассмотрим преобразование в виде треугольника ветвей с сопротивлениями эквивалентную трехлучевую звезду. Формулы преобразования имеют следующий вид: 
Преобразования ветвей трехлучевой звезды в эквивалентной треугольник. Формулы преобразования источника тока, и наоборот, имеют следующий вид. 
, 
Вопросы для самоконтроля.
1. Запишите закон Ома для пассивного участка цепи через проводимость.
2. Запишите закон Ома для активного участка цепи через проводимость.
3. Чему равно эквивалентное сопротивление трех параллельно соединенных резисторов?
4. Определить эквивалентное сопротивление трех резисторов с равными сопротивлениями, соединенных параллельно.
5.
