Последовательное соединения элементов R, L, C называется последовательным колебательным контуром, в нем возможен резонанс напряжения. Резонансом напряжения называется такой режим в колебательном контуре, при котором частота источника э.д.с.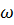 
равна частоте собственных колебании контура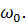 
Выходное напряжения u=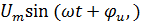 
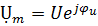
1.При резонансе напряжения, входное сопротивление становится чисто резистивным, реактивное входное сопротивление становится число резистивным, реактивное входное сопротивление равно нулю
Ẕ=R+j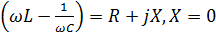 
, 
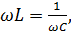Ẕ=R.
2.резонансная частота контура определяется из соотношения 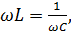т.е.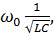 
3.Так как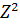 
= 
+ 
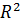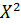, X=0, Z=R.полное сопротивление минимально, тогда токи в цепи 
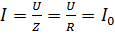и активная мощность в режиме резонанса максимальны P= 
.
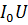4. 
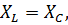
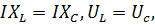U=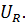 
Напряжения на реактивных элементах равны величине и противоположны по направлению. Реактивное мощности тоже равны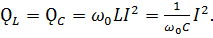 
5. 
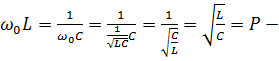характеристическое или волновое сопротивление контура.
6. Отношение напряжении на реактивных элементах к приложенному напряжению, или отношение реактивных мощностей к активной мощности в режиме резонанса называется добротностью контура
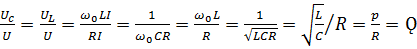-добротность контура.
Добротность контура указывает во сколько раз напряжение на индуктивности и емкости при резонансе больше, чем напряжение приложенное к цепи. Добротность обычных контуров бывает порядка от 50 до 300. Это означает, что напряжение и мощность реактивных элементов в десятки и в сотни раз превышает напряжение и мощность источника. Векторная диаграмма в момент резонанса.
Параллельное соединение элементов R,L,C называется параллельным колебательным контуром, в нем возможен резонанс токов. Резонанс токов наступает, когда выходная проводимость реактивная равна нулю.
……………………
Ток в неразветвленной части: ḻ= 
где Y-входная комплексная проводимость.
Y=G-j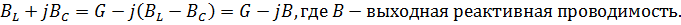 
При резонансе токов B=0?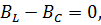 
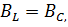
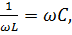
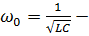резонансная частота контура.
При резонансе U⦁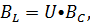 
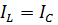ток через индуктивный элемент равен по модулю току через емкостный элемент и находится в противофазе и могут превышать входной ток.
Добротность параллельного контура, показывает во сколько раз ток в реактивных элементах при резонансе больше тока на входе контура.
Ǫ=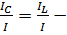 
добротность параллельного контура, показывает во сколько раз ток в реактивных элементах при резонансе больше тока на входе контура.
Частотные характеристики параллельного колебательного контура.
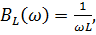
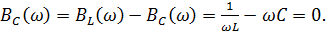
Частотное характеристики резонансных контуров.
Пусть к цепи пртложенно синусоидальное напряжение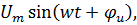 
амплитуда которого постоянна, а частота изменяется от изменение частоту проводит к изменению параметров цепи. Меняется реактивное сопротивление, полное сопротивление, а также уголь 
Зависимость действующих или амплитудных значений тока I и напряжении 
от частоты называется резонансными кривыми.
= 
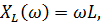
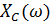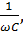X()=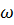 
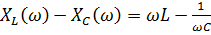называется частотным характеристиками цепи, а зависимости I(), 
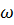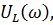
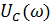называется резонансными кривыми.
……………………………
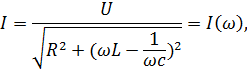
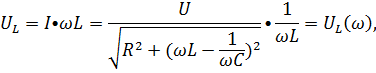
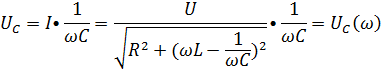
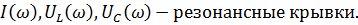
Для удобства сравнения резонансных кривых друг с другом будем рассматривать зависимости: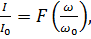 
где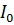 
ток при резонансе, 
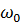-резонансное частота.
.
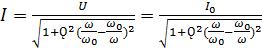Чем больше Ǫ, тем острее резонансная кривая, тем лучше избирательные свойства цепи.
……………………
Вопросы для самоконтроля:
1. Условия для наступления в цепи резонанса напряжении.
2. Чему равно входное сопротивление цепи в момент резонанса.
3. Векторная диаграмма цепи в момент резонанса
4. Добротность контура. Применение явления резонанса.
5. Условия резонанса тока.
6. Частотные характеристики последовательно колебательного контура.
7. Полоса пропускания контура и ее связь с добротностью контура.
Литература:
1.Атабеков Г.И. Основы теории цепей.-М.: Энергия, 2006-544с.
2.бакалов В.П., Воробинко П.П. Крук Б.И Теория электрических цепей.-М.: Радио и связь, 1998-440с.
3.Под редакцией Ионкина П.Теоритические основы электротехники. М.:
Высшая школа.1976-545с.
4.Зевеке Г.В Ионкин П.А и др. Основы теории цепей. М.:Энергия, 1989-528с.
Планы практических занятий
Тема №1. Эквивалентное преобразования электрических цепей. Преобразование треугольника сопротивлений в звезду сопротивлении. Определении эквивалентных сопротивлении
Повторить эквивалентные преобразования простейших резистивных цепей: последовательное, параллельное, смешанное соединение цепей. Изучить преобразование треугольника сопротивление в звезду. Формулы преобразование. Закрепить и уметь применять эквивалентные преобразования при решении практических задач.
Задания: Изучить эквивалентные преобразование электрических цепей.
Уметь рассчитывать эквивалентные сопротивления цепей. Преобразование треугольника сопротивлении в звезду. Уметь преобразовывать сложные электрические цепи в простые в помощью эквивалентных преобразований.
Решение задач 1.2, 1.3, 1.8, 1.10, 1.50 Л [1]
Основные вопросы:
Определить эквивалентное сопротивление трех параллельно соединенных резисторов. Получить формулу «разброса» для нахождения токов в параллельных ветвях. Рассчитать цепь при смешанном соединении резисторов.
Методические рекомендации к выполнению:
Изучить эквивалентные преобразования «треугольника» сопротивлений в звезду. Вспомнить простейшие эквивалентные преобразования: последовательное, параллельное, смешанное соединение цепей.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема№2. Преобразование звезды сопротивление в треугольник сопротивлений. Источники э.д.с. и тока. Эквивалентные преобразование источников.
Цели занятия:
Рассмотреть и закрепить преобразование «звезды» сопротивлений в треугольник сопротивлений. Рассмотреть эквивалентные преобразование источников. Закрепить и уметь применить знания при решении практических задач.
Задания: Решить задачи 1.51, 1.52, 1.53, 1.54, 1.55, 1.56, 1.58,1.59 Л[1].
Основные вопросы:
Особенности преобразования звезды сопротивлений в треугольник.
Эквивалентные преобразование источника тока в источник э.д.с..
Эквивалентные преобразование источника э.д.с. в источник тока.
Методические указания к выполнению:
Изучить эквивалентные преобразования сопротивлений по схеме «звезда» в треугольник. Вспомнить простейшие эквивалентные преобразования: последовательное, параллельное, смешанное соединение цепей.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема№3. Электрические цепи гармонического тока. Определение эквивалентных комплексных сопротивлений. Алгебраическая и показательная формы. Треугольник проводимостей.
Цель занятия:
Рассмотреть и закрепить электрические цепи гармонические тока. Уметь определять выражение комплексного сопротивления и комплексной проводимости, модуль, аргумент. Уметь работать с комплексными числами, производить действия с комплексными числами уметь переходить из показательной формы в алгебраическую, из алгебраической в показательную. Изучить законы Ома и Кирхгофа в комплексной форме.
Задания: Решить задачи 2.2, 2.3, 2.4, 2.5, 2.8, 2.18, 2.19,2.24, 2.30, 2.32, 2.34 Л[1].
Основные вопросы:
Изображения синусоидальной функции вращающимся вектором.
Изображения синусоидальной функции комплексным числом.
Полное, активное и реактивное сопротивление. Треугольник сопротивлений.
Полная, активная и реактивная проводимость. Треугольник проводимостей.
Методические указания к выполнению:
Изучить и закрепить особенности гармонического тока. Решить задачи для закрепления данного материала. Уметь определить комплексное, полное, активное и реактивное сопротивление. Уметь определять комплексную, полную, активную, реактивную проводимость. Аргумент комплексного сопротивления. Рассмотреть законы Ома и Киргхгофа в комплексной форме.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №4. Методы представления гармонических функций. Символический метод. Пассивные элементы гармонического тока. Векторная диаграмма. Топографическая диаграмма. Измерение мощностей.
Цель занятия:
Рассмотреть методы представления гармонической функции.
Представление гармонической функции графиком во временной области. Изображение гармонической функции вращающимся вектором. Изображение гармонической функции комплексным числом. Изучить построение векторных и топографических диаграмм. Рассмтреть измерение мощностей в цепи гармонического тока.
Задания: Решение задачи 2.43, 2.48 2.49, 2.50, 2.51, 2.52, 2.53 Л[1].
Основные вопросы:
Рассмотреть методы представления гармонических функций.
Методы расчета цепей гармонического тока в комплексной форме. Символический метод. Векторные диаграммы отдельных элементов, векторные диаграммы отдельных электрических цепей. Топографические диаграммы. Измерение мощности ваттметром.
Методические указания к выполнению:
Изучить методы расчета цепей гармонического тока. Особенности применения методов расчета постоянного тока для решения задач гармонического тока.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №5. Частотные характеристики электрических цепей. Комплексные передаточные функции линейных электрических цепей. Частотные характеристики последовательного колебательного контура. Частотные характеристики параллельного колебательного контура.
Цель занятия: Изучить комплексные передаточные характеристики электрических цепей: комплексную передаточную функцию по току, комплексное передаточное сопротивление и комплексная передаточная проводимость. Изучить построение амплитудно-частотную и фаза – частотных характеристик. Изучить и закрепить частотные характеристики резонансные колебательного контура.
Занятия: Построить амплитудно-частотную и фазо – частотную характеристики комплексной передаточной функцию по напряжению последовательного колебательного контура для различных значении добротности, изменяя частоту в пределах 0.25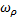 
до 2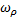 
.
Построить амплитудно-частотную и фаза – частотную характеристики комплексной передаточной функцию по току параллельного колебательного контура изменяя частоту в пределах 0.25 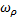до 2 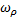, для различных значений добротности.
Методические рекомендации к выполнению:
Изучить частотные характеристики электрических цепей, уделив особое внимание на построение амплитудно-частотную и фаза – частотную характеристик.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №6 Частотные характеристики реактивных двухполюсников,
Цель занятия:
Изучить и закрепить общие свойства реактивных двухполюсников. Изучить частотные зависимости входных функции цепи: входного комплексного сопротивления и входной комплексной проводимости. Изучить канонические схемы реактивных двухполюсников.
Задание: Построить зависимости входных функций от частоты простых двухполюсников, состоящий из одного элемента: одного индуктивного и одного емкостного элемента(одноэлементные двухполюсники).
Построить функции входного сопротивления и входной проводимости двухэлементных двухполюсников.
Построить функции входного сопротивления и проводимости трехэлементных двухполюсников.
Методические рекомендации к выполнению:
Изучить и закрепить частотные характеристики реактивных двухполюсников.
Уметь строить зависимости входных функции от частоты.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №7. Особенности анализа индуктивно связанных элементов. Расчет по законам Кирхгофа. Метод контурных токов. Воздушный трансформатор.
Цель занятия:
Изучить и закрепить основные методы анализа цепей с индуктивно связанными элементами. Изучить особенности явлений, происходящих в электрических цепях с индуктивно связанными элементами. Уметь определять коэффициент взаимной индукции, составлять уравнения равновесия, уметь определять одноименные зажимы и построения векторных диаграмм.
Задания. Изучить методы анализа цепей с индуктивными связями: расчет по законом Кирхгофа и метод контурных токов. Изучить особенности анализа этих цепей. Изучить методы развязки индуктивно связанных цепей. Изучить частотные характеристики связанных колебательных контуров.Построить амплитудно-частотную характеристику связанных колебательных контуров.
Методические рекомендации к выполнению:
Изучить и закрепить особенности индуктивно связанных цепей. Уметь применять законы Кирхгофа, метод контурных тоов. Для инфуктивно связанных цепей подходят только эти методы расчета.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №8. Методы расчета и измерение мощностей в трехфазных цепях.
Цель занятия:
Закрепить методы симметричных и несимметрических трехфазных цепей. Закрепить особенности методы симметричных составляющих для расчета несимметрических трехфазных цепей. Изучить свойство трехфазных цепей в отношении симметричных составляющих токов и напряжений. Изучить методы измерения мощности в трехфазных цепях.
Задания:
Произвести расчет трехфазной цепи при поперечной несимметрий.
Произвести расчет трехфазной цепи при продольной несимметрии.
Произвести расчет мощности трехфазной цепях.
Методические рекомендации к выполнению:
Изучить методы анализ симметричных и несимметрических трехфазных цепей.
Изучить метод симметрических составляющих для решения несимметричных режимов в трехфазных цепях.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
