В основу метода положено то, что для каждого независимого узла электрической схемы можно составить уравнение по первому закону Кирхгофа (узловые уравнения), а для каждого независимого контура – по второму закону Кирхгофа (контурные уравнения).
Рассмотрим схему (рис. 3.3).
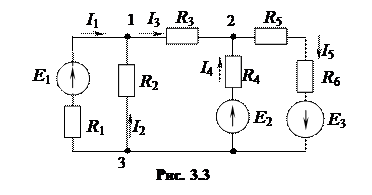
Выберем условно положительные направления токов. Если в простых цепях обычно можно определить истинные направления токов, то в сложных цепях это сделать не всегда возможно, так как источники действуют в разных направлениях и могут компенсировать друг друга, поэтому направления токов выбираем произвольно. Если в ветви есть источник ЭДС, то часто направление тока задают совпадающим с направлением источника, но это не обязательно.
Определяем количество независимых узлов и контуров.
В рассматриваемой схеме пять ветвей т = 5 и три узла п = 3(один фиктивный), следовательно, количество независимых узлов N = п – 1 = 3 – 1 = 2; количество независимых контуров К = т – (п – 1) = 5 – (3 – 1) = 3.
Таким образом, для данной схемы можно составить два узловых и три контурных уравнения.
Составим уравнения для узлов 1 и 2, считая положительными токи, текущие от узла,
;
.
Для расчета пяти токов необходимо иметь пять уравнений. Недостающие три уравнения составляем по второму закону Кирхгофа для контуров:
Е 1 – R 2 – R 1; R 2 – R 3 – R 4 – E 2; R 4 – R 5 – R 6 – E 3 – E 2,
выбрав направление обхода контуров по часовой стрелке.
;
;
.
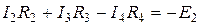Итак, мы получили пять уравнений с пятью неизвестными. Решая их любым известным в математике способом, находим токи в ветвях.
Достоинством этого метода является то, что уравнения составляются непосредственно для искомых величин, в результате не требуется определения промежуточных или фиктивных параметров.
К недостаткам следует отнести то, что при расчете этим методом составляется большое количество уравнений, каждое из которых включает в себя только часть токов. В результате получается система с большим количеством нулевых членов, что затрудняет применение матричных методов.
Метод контурных токов
Метод контурных токов позволяет уменьшить число уравнений, составляемых по законам Кирхгофа до числа независимых контуров.
Метод контурных токов основан на том свойстве, что ток в каждой ветви может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих в этой ветви.
Рассмотрим электрическую цепь (рис. 3.4), аналогичную той, что рассматривали в предыдущем случае.
Определим число независимых контуров:
 |
К = т – (п – 1) = 5 – (3 – 1) = 3.
Считаем, что в каждом контуре протекает свой, независимый от других контуров, ток. Направление контурных токов обозначаем круговой стрелкой. Выберем направление контурных токов по часовой стрелке и запишем для каждого контура уравнение по второму закону Кирхгофа с использованием контурных токов, считая положительным направлением для каждого контура направление контурного тока:
.
Эту систему уравнений можно привести к следующему виду:
.
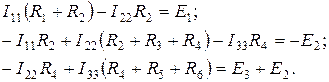При расчете цепей методом контурных токов удобнее пользоваться готовой математической моделью, которая представляет собой систему линейных алгебраических уравнений:
Здесь R 11, R 22, R 33 – собственные сопротивления контуров, равные сумме всех сопротивлений, входящих в контур:
;
;
.
Все остальные сопротивления являются взаимными:
R 12 = R 21 = R 2 – взаимное сопротивление между первым и вторым контурами;
R 23 = R 32 = R 4 – взаимное сопротивление между вторым и третьим контурами;
R 13 = R 31 = 0; – взаимное сопротивление между первым и третьим контурами.
Из схемы можно видеть, что первый и третий контуры не имеют общей ветви, а граничат только через узел, поэтому их взаимное сопротивление равно нулю
Е 11 = Е 1; Е 22 = – Е 2; Е 33 = Е 3 + Е 2 – контурные ЭДС.
Если действие э.д.с. совпадает с направлением контурного тока, то ЭДС имеет знак «плюс», если не совпадает – «минус».
При использовании математической модели следует направления всех контурных токов выбирать одинаковыми. В этом случае члены, расположенные по главной диагонали и содержащие собственные сопротивления контуров, будут положительны, а члены, содержащие взаимные сопротивления, – отрицательны.
Если число уравнений больше двух, то систему удобнее решать матричным методом.
Составим главный определитель системы
.
Частные определители получим, заменяя соответствующие столбцы матриц столбцами свободных членов
.
Контурные токи находим из выражений:
; 
; 
.
Для того чтобы определить истинные токи в ветвях, следут пользоваться следующими правилами. Если в ветви протекает только один контурный ток, то истинный ток равен этому контурному току, причем, если условно положительное направление истинного тока совпадает с направлением контурного тока, то ставим знак контурного тока, если не совпадает – противоположный. Если в ветви протекает два контурных тока, то за положительный принимаем тот, направление которого совпадает с направлением истинного тока. Для заданной схемы истинные токи определятся выражениями:
; 
; 
; 
; 
.
Достоинством этого метода по отношению к предыдущему является то, что количество уравнений, составляемых по законам Кирхгофа, уменьшается.
К недостаткам можно отнести введение в расчеты фиктивных величин – контурных токов, через посредство которых находят истинные токи.
Метод узловых потенциалов
Метод узловых потенциалов заключается в том, что сначала находят потенциалы всех узлов схемы, а потом по известным потенциалам, используя обобщенный закон Ома, определяют токи в ветвях.
Количество уравнений, составляемых по методу узловых потенциалов, определяется числом независимых узлов N = n – 1.
Заземляем один из узлов. Как правило, заземляется узел, в котором сходится больше ветвей. Заземлим узел 3 (рис. 3.4), то есть полагаем 
.
Выразим токи в ветвях через потенциалы.
; 
;
; 
; 
.
Здесь
; 
; 
; 
; 
– проводимости ветвей.
Для узлов 1 и 2 составим уравнения по первому закону Кирхгофа:
;
;
Подставим в эти уравнения выражения для токов, раскрывая скобки:
;
.
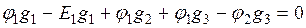Преобразуем выражения:
;
.
Эту систему уравнений можно записать в общем виде и при расчетах сразу использовать готовую модель:
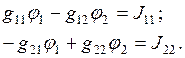
Здесь 
и 
– собственные проводимости узлов, они определяются суммой проводимостей всех ветвей, сходящихся в данном узле;
– взаимные проводимости, то есть проводимости ветвей, расположенных между соответствующими узлами;
; 
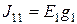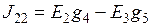– узловые токи.
Для того чтобы рассчитать узловые токи, из всех ветвей, сходящихся в данном узле, выбираем те, которые содержат источники, умножаем ЭДС каждого источника на проводимость ветви, в которой он находится. Если в одном узле сходятся несколько ветвей с источниками, как, например, в узле 2, то находим их алгебраическую сумму. Если источник направлен к узлу, то узловой ток берем со знаком «плюс», если от узла – «минус».
Решая полученную систему любым способом, находим потенциалы узлов 1 и 2, и, подставляя их в полученные выражения для токов, находим токи.
Достоинство данного метода состоит в том, что он позволяет свести количество уравнений в схеме к минимуму.
Недостаток состоит в следующем. Рассчитывая цепь методом узловых потенциалов, мы работаем с проводимостями ветвей. Проводимость – величина обратная сопротивлению, и при больших значениях сопротивлений проводимости малы. Отсюда точность метода узловых потенциалов ниже, чем у метода контурных токов, поэтому метод узловых потенциалов целесообразно применять тогда, когда число уравнений, составляемых по методу узловых потенциалов, меньше, чем по методу контурных токов, как в нашем случае.
Метод двух узлов
Метод двух узлов является частным случаем метода узловых потенциалов. Этот метод применяется в том случае, когда в схеме имеется несколько ветвей, присоединенных к одной паре узлов. В частности, этот метод позволяет определить напряжение, подаваемое на нагрузку, если она питается от нескольких источников, соединенных параллельно.
Рассмотрим схему, в которой три источника работают на одну нагрузку R 4 (рис. 3.5).
 |
Воспользуемся методом узловых потенциалов. Выразим потенциал точки а через потенциал точки b вдоль каждой ветви:
.
Перенесем потенциал 
в левую часть. Разность потенциалов точек a и b представляет собой напряжение между узлами Uab:
;
;
;
.
Отсюда выразим токи:
; 
;
; 
.
Запишем первый закон Кирхгофа для узла а:
.
Подставим сюда выражения для токов, раскрывая скобки,
или
.
Отсюда
.
Эта формула позволяет определить напряжение между двумя узлами при наличии нескольких параллельных ветвей с источниками. При этом справедливо правило: если ЭДС направлена в сторону узла а, то она положительна, если от узла – отрицательна.
Метод наложения
В основу метода положен принцип наложения: ток в любой ветви разветвленной линейной электрической цепи с несколькими источниками может быть получен как алгебраическая сумма токов, вызываемых в этой ветви каждым источником в отдельности.
Метод расчета токов в электрической цепи, основанный на определении токов в одной и той же ветви при поочередном воздействии всех ЭДС и последующем алгебраическом сложении этих токов называется методом наложения.
При расчете методом наложения электрической цепи с реальными источниками следует учитывать внутренние сопротивления источников ЭДС.
Как правило, метод наложения используется в том случае, если в цепи имеется два источника.
Рассмотрим применение этого метода на примере схемы (рис. 3.6).
Задача состоит в том, чтобы найти токи в ветвях I 1, I 2, I 3 методом наложения.
Задаемся условно положительными направлениями токов в ветвях.
1. Исключаем источник Е 2, тогда в цепи будет действовать только один источник Е 1, и схема примет вид (рис. 3.7)
Так как в цепи действует только один источник, мы можем задать истинные для данной схемы направления частичных токов I 1’, I 2’, I 3’.
Для расчета этих токов используем любой метод расчета простых цепей, например, метод эквивалентных преобразований.
 |
Находим эквивалентное сопротивление цепи
.
Зная величины Е 1 и Rэк, находим ток источника
.
Для определения токов I 2’ и I 3’ найдем напряжение между точками a и b.
.
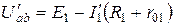Используя найденное напряжение, по закону Ома находим токи I 2’ и I 3’
; 
.
 |
2. Исключаем источник Е 1, тогда в цепи будет действовать только один источник Е 2 и схема примет вид (рис. 3.8).
Зададимся истинными направлениями частичных токов в ветвях для данной схемы I 1’’, I 2’’, I 3’’ и выполним расчеты, аналогичные предыдущим.
Находим эквивалентное сопротивление цепи
.
Зная величины Е 2 и R”эк, находим ток источника
.
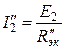Для определения токов I 1” и I 3” найдем напряжение между точками a и b
.
Находим токи I 1” и I 3”:
; 
.
3. Находим истинные токи в ветвях как алгебраическую сумму токов, создаваемых каждым источником:
; 
; 
.
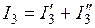При этом частичный ток берется положительным, если его направление совпадает с выбранным условно положительным направлением истинного тока, и отрицательным, если его направление противоположно.
