На практике приходится работать со схемами, в которых одни элементы соединены последовательно, другие – параллельно. Такое соединение называется смешанным.
 |
Рассмотрим простейшую схему смешанного соединения (рис. 2.4).
Ветви с сопротивлениями R 2 и R 3 подсоединены к одним и тем же узлам и находятся под одним напряжением U 2 , то есть, соединены параллельно. Параллельный участок соединен последовательно с сопротивлением R 1, которое находится под напряжением U 1. Тогда по второму закону Кирхгофа для данной цепи можно записать
.
По первому закону Кирхгофа
.
Эквивалентное сопротивление цепи найдем, используя правила преобразования последовательных и параллельных участков,
.
В многоэлементных электрических цепях со смешанным соединением иногда бывает невозможно сразу выделить участки с последовательным или параллельным соединением. В этом случае эквивалентное сопротивление всей цепи находят поэтапно, рассчитывая эквивалентные сопротивления отдельных участков, последовательно упрощая схему, свертывая ее.
Рассмотрим метод свертывания на примере схемы (рис. 2.5).
Найдем эквивалентное сопротивление этой цепи методом свертывания.
Свертывание цепи всегда начинают с ветвей, наиболее удаленных от источника. Действительно, если мы рассмотрим участки с сопротивлениями 
,R 4, R 5, то не сможем выделить ни последовательного, ни параллельного соединений, тогда как ясно видно, что 
соединены последовательно. Находим их эквивалентное сопротивление
.
После такой замены схема примет вид (рис. 2.6).
В этой схеме сопротивления 
соединены параллельно, находим
.
Схема принимает вид (рис. 2.7).
Далее последовательно находим сопротивления:
; 
; 
;
.
Определив эквивалентное сопротивление, можно выполнять расчет токов и напряжений электрической цепи.
Преобразование треугольника сопротивлений
В эквивалентную звезду
В некоторых случаях в электрических цепях существуют такие соединения элементов, которые не поддаются расчетам по методу свертывания, так как не содержат ни последовательно, ни параллельно соединенных элементов. Примером такой схемы может служить мостовая схема (рис. 2.8).
Для того чтобы найти эквивалентное сопротивление такой схемы, применяют преобразование треугольника сопротивлений в эквивалентную звезду.
Треугольником сопротивлений называют такое соединение трех элементов, при котором они образуют замкнутый контур, причем между каждой парой элементов имеется узел (рис. 2.9).
Трехлучевой звездой сопротивлений называют такое соединение элементов, при котором одним концом они подсоединены к одному узлу, а другие концы соединяются с остальной цепью (рис. 2.10).
 |
Заменим схему треугольника сопротивлений схемой трехлучевой звезды (рис. 2.11). Обозначим сопротивления звезды
, а сопротивления треугольника 
. Замена треугольника сопротивлений на трехлучевую звезду будет эквивалентной при условии, что такая замена не изменяет потенциалов узловых точек 1, 2, 3, являющихся вершинами треугольника и концами лучей звезды. Кроме того, такая замена не должна влиять на режим работы остальной части цепи, то есть токи, напряжения и мощности в остальной цепи остаются неизменными.
Докажем возможность такого перехода. Приведенные на рис. 2.11 схемы должны оставаться эквивалентными для любого режима работы цепи. Одним из таких режимов может быть равенство нулю тока I 1, что соответствует обрыву общего провода, ведущего к точке 1. Тогда между точками 2 и 3 в схеме треугольника окажутся две параллельные ветви с сопротивлениями R 23 и R 31 + R 12.
Общее сопротивление между этими точками определится как
.
В схеме звезды между этими точками включено сопротивление R 3 + R 2.
По условию эквивалентности токи I 2 и I 3 в обеих схемах равны, напряжения между точками 2 и 3 равны, следовательно, должны быть равны и сопротивления, то есть выполняться равенство
.
Положим теперь I 2 = 0, получим
.
При I 3 = 0, получим
.
Решая совместно эти три уравнения, получим выражения, связывающие сопротивления трехлучевой звезды с сопротивлениями треугольника
; 
; 
. (2.1)
Следовательно, треугольник сопротивлений 
можно заменить трехлучевой звездой с сопротивлениями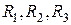 
.
В некоторых случаях удобнее для расчетов выполнить преобразование звезды в треугольник. Чтобы рассчитать сопротивления сторон треугольника, зная сопротивления лучей звезды, будем исходить из формул (2.1).
Разделим третье уравнение на первое, получим
.
Теперь разделим третье уравнение на второе, получим
.
Из этих выражение выразим сопротивления R 23 и R 31 через R 12:
; 
.
Подставим эти выражения в первое уравнение:
.
Отсюда найдем R 12:
.
Аналогично можно получить выражения для R 23 и R 31:
; 
.
Чаще при преобразовании звезды в треугольник пересчитывают не сопротивления, а проводимости ветвей, пользуясь формулами:
; 
; 
,
где g 1, g 2, g 3 – проводимости лучей звезды, g 12, g 23, g 31 – проводимости сторон треугольника.
Контрольные вопросы и задания
1. Какое соединение элементов называется последовательным?
2. Каким правилам подчиняются ток и напряжение при последовательном соединении элементов?
3. Как определить эквивалентное сопротивление при последовательном соединении?
4. Какое соединение элементов называется параллельным?
5. Каким правилам подчиняются ток и напряжение при параллельном соединении элементов?
6. Как определить эквивалентное сопротивление и эквивалентную проводимость при параллельном соединении?
7. Какое соединение элементов называется смешанным?
8. Каким правилам подчиняется цепь при смешанном соединении?
9. В чем состоит метод свертывания цепи?
10. Опишите порядок свертывания цепи.
11. Дайте определение треугольника сопротивлений и трехлучевой звезды сопротивлений.
12. При каких условиях замена одного участка электрической цепи другим будет эквивалентной?
