Введение
Роль и значение электрической энергии в науке, технике, быту в настоящее время очень велики. Электричество является основой развития всех отраслей техники, базой для развития промышленности, транспорта, сельского хозяйства, электросвязи. Столь широкому распространению применения электрической энергии способствовало удобство передачи электромагнитной энергии на расстояние и удобство преобразования ее в другие виды энергии: механическую, тепловую, световую, химическую и т. д.
Предметом курса «Теория электрических цепей» является изучение как с качественной, так и с количественной сторон электромагнитных процессов, происходящих в электрических и магнитных цепях.
Физические процессы, происходящие в электрических цепях можно изучать как с точки зрения теории электрических цепей, так и с точки зрения теории электромагнитного поля.
Теория цепей исходит из приближенной замены реального электротехнического устройства идеализированной схемой замещения и позволяет с достаточной для инженерных целей точностью определять токи, напряжения, мощности различных участков электрических цепей.
Теория поля изучает изменение электрических и магнитных величин от точки к точке в пространстве и времени. Она исследует напряженности электрического и магнитного полей и с их помощью такие явления, как излучение электромагнитной энергии, распределение зарядов, плотности тока и т. д.
Разграничение областей применения теории цепей и теории поля является условным. Например, процессы распространения электрических сигналов в линиях электропроводной связи исследуются как методами теории цепей, так и методами теории поля.
В процессе изучения дисциплины «Теория электрических цепей» студенты должны овладеть методами анализа электрических цепей с сосредоточенными параметрами в установившемся и переходном режимах, ознакомиться с основами анализа линейных цепей с распределенными параметрами и нелинейных резистивных цепей, освоить основные методы синтеза линейных цепей с сосредоточенными параметрами.
В курсе «Теория электрических цепей» рассматриваются физические процессы, происходящие в электрических цепях, математические модели, позволяющие дать количественную оценку этих процессов, методы анализа и синтеза электрических цепей. Знание теории цепей необходимо для успешного усвоения студентами всех последующих дисциплин, а также для работы в сфере обслуживания систем и сетей связи и при исследованиях, расчетах и проектировании вновь создаваемых систем. Теория электрических цепей образует фундамент, на котором базируется вся профессиональная творческая деятельность бакалавра техники связи. Залогом успеха в этой деятельности является хорошее усвоение аппарата анализа электрических цепей и умение применять его для решения практических задач.
Основные понятия и законы линейных электрических цепей
Основные определения, относящиеся к линейным
Электрическим цепям
Электрической цепью называется совокупность устройств и элементов, соединенных между собой и обеспечивающих прохождение электрического тока. То есть это совокупность источников и приемников энергии, соединительных проводов и измерительных приборов.
Источники электрической энергии – это устройства, в которых происходит преобразование различных видов энергии (тепловой, химической, механической) в электрическую.
Приемники электрической энергии (потребители, нагрузка) – это устройства, в которых электрическая энергия преобразуется в другие виды энергии.
Электрические цепи, в которых получение и преобразование электрической энергии происходят при неизменных во времени токах и напряжениях, называются цепями постоянного тока. Электрические цепи, в которых ток и напряжение изменяются с течением времени по величине и направлению называются цепями переменного тока.
Электрические цепи подразделяются на линейные и нелинейные.
Линейной электрической цепью называется цепь, состоящая только из линейных элементов. Если в цепи имеется хотя бы один нелинейный элемент, то цепь будет нелинейной.
Линейные элементы – это элементы электрической цепи, сопротивление которых не зависит от проходящего по ним тока или напряжения на их зажимах. Вольт-амперная характеристика (зависимость тока от напряжения) для линейных элементов представляет собой прямую линию; для нелинейных – кривую.
Любую электрическую цепь и происходящие в ней процессы можно описать с помощью понятий:
ток I [ A ], Ампер;
напряжение U [ B ], Вольт;
электродвижущая сила (ЭДС) Е [ B ], Вольт;
сопротивление R или r [ Ом ], Ом;
проводимость G или g [См ], Сименс;
индуктивность L [ Гн ], Генри;
емкость С [ Ф ], Фарада.
Основной целью изучения электрических цепей является анализ режимов работы этих цепей. На основе такого анализа можно определить, при каких условиях и с какой эффективностью будет работать радиотехническое оборудование. В большинстве случаев эта цель достигается определением токов на всех участках электрической цепи. Зная токи, можно найти напряжения и мощности отдельных элементов.
Для удобства расчетов электрическую цепь заменяют схемой замещения.
Схема замещения или электрическая схема – это графическое изображение электрической цепи с помощью условных знаков. Топологию электрической цепи определяют геометрические элементы схемы, которыми являются ветви, узлы и контуры.
Ветвь образуется одним или несколькими последовательно соединенными элементами цепи (рис. 1.1). По всем элементам ветви протекает один и тот же ток.
 |
Узел – место соединения трех и более ветвей. На электрических схемах узел обозначают точкой, как показано на рис. 1.2, а,б.
  |
По своему электрическому смыслу схемы а) и б) идентичны и содержат один узел. Участки цепи между точками 1 и 2, 2 и 3, 3 и 4 не содержат элементов, следовательно, не являются ветвями. Представив схему б) в виде а), получим один узел, поэтому точки 2, 3, 4 называют фиктивными или устранимыми узлами.
Узел является независимым, если к нему подходит хотя бы одна ветвь, не входящая в другие узлы. Число независимых узлов всегда на единицу меньше, чем общее число узлов в схеме. Если общее число узлов п, то число независимых узлов N = n – 1.
Исходя из понятия узла, ветвь можно охарактеризовать как участок цепи между двумя соседними узлами.
Контур – это любой замкнутый путь, проходящий по нескольким ветвям.
Для расчета электрических цепей используются независимые контуры. Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
Число независимых контуров рассчитывается по формуле
К = т – (п – 1) = т – N.
Здесь т – число ветвей.
Для примера рассмотрим контур, приведенный на рис. 1.3.
Данная схема содержит 4 ветви, 6 контуров и 2 узла. Линии схемы, в которых отсутствуют элементы цепи, не являются ветвями. Так как линия 2– 
не является ветвью, то узел является «фиктивным», или устранимым узлом.
Так как данная схема содержит четыре ветви и два узла, следовательно,
независимых узлов: N = n – 1 = 2 – 1 = 1;
независимых контуров: К = т – (п –1) = 4 – (2 – 1) = 3.
Ток, напряжение, мощность
Электрический ток есть упорядоченное движение электрических зарядов как положительных q+, так и отрицательных q -. Интенсивность, или сила тока определяется количеством электрического заряда q = q+ + q-, прошедшего через поперечное сечение проводника за единицу времени:
Следовательно, ток представляет собой скорость изменения заряда во времени. Следует отметить, что величина заряда весьма мала, отрицательный заряд одного электрона qе = 1,6·10-19 Кл.
 |
Ток – величина алгебраическая, то есть имеет знак положительный или отрицательный. В физике за положительное направление тока условно принимается направление движения положительного заряда, в противном случае ток отрицателен. В теории электрических цепей нам часто неизвестно истинное направление движения зарядов, поэтому задаются условно положительным направлением тока. Условно положительное направление тока на участке цепи выбирается произвольно и обозначается стрелкой, как это показано на рис. 1.4.
Выбранное направление тока не означает реального направления положительных зарядов, а только придает знаку тока определенный смысл. На рис. 1.4 положительное направление тока от точки 1 к точке 2. Кроме стрелки, это направление можно обозначить при помощи индексов: i 12. Первая цифра показывает точку, от которой течет ток, вторая – точку, к которой течет ток. Очевидно, что i 12 = – i 21.
Каждая точка электрической цепи имеет свой потенциал. Электрический потенциалφ численно равен работе, совершаемой силами поля по переносу единичного положительного заряда из бесконечности в данную точку.
Ток всегда протекает от точки с большим потенциалом к точке с меньшим потенциалом. Если потенциалы двух точек одинаковы, то ток между ними протекать не будет.
Прохождение электрического тока, то есть перенос заряда в цепи, связано с преобразованием или потреблением энергии W.
Напряжением называют количество энергии, затрачиваемой на перемещение единицы заряда из одной точки в другую:
Для напряжения, как и для тока, произвольно выбирают условно положительное направление, чаще всего его выбирают совпадающим с положительным направлением тока и указывают стрелкой (рис. 1.4). При согласованном выборе полярности тока и напряжения, очевидно, достаточно ограничиться только указанием направления тока.
Для положительного напряжения стрелка указывает направление от большего потенциала φ 1 к меньшему φ 2. Таким образом, напряжение можно рассматривать как разность потенциалов двух точек цепи 
.
Энергия. Если к участку цепи приложить напряжение U, то через этот участок будет проходить электрический заряд q. Энергия, затраченная на перемещение заряда q на участке цепи с напряжением U в интервале времени от t = – ∞, где энергия принимается равной нулю, до рассматриваемого момента времени t 1 определяется соотношением
Энергия – величина положительная.
Мощность – это скорость изменения энергии во времени. Мгновенная мощность определяется выражением
Мгновенная мощность – величина алгебраическая. Знак мощности определяется знаками мгновенных значений напряжения и тока: при совпадении знаков напряжения и тока мощность положительна, что соответствует потреблению энергии рассматриваемым участком цепи. При несовпадении знаков мощность отрицательна, что свидетельствует о том, что энергия отдается участком цепи.
Все элементы электрической цепи подразделяются на активные и пассивные. Активные элементы – это источники электрической энергии, пассивные элементы – это сопротивление, индуктивность, емкость.
Активные элементы
К активным элементам электрических цепей относятся источники ЭДС и источники тока.
Источники ЭДС
Идеализированный источник ЭДС – это активный элемент с двумя зажимами, напряжение на которых не зависит от проходящего через источник тока. Перемещение зарядов в источнике от точки с меньшим потенциалом к точке с большим потенциалом осуществляется за счет сторонних сил, присущих источнику.
 |
Обозначение идеализированных источников ЭДС на электрических схемах показано на рис. 1.5.
Электродвижущая сила (ЭДС) – это количество энергии, затраченное сторонними силами на перенос единичного положительного заряда от меньшего потенциала к большему
.
За положительное направление э.д.с. принимается направление возрастания потенциала (рис. 1.6). Таким образом, положительные направления ЭДС и напряжения всегда противоположны.
Численно ЭДС равна разности потенциалов между выводами источника при разомкнутой цепи.
Если внутри источника ЭДС не содержится пассивных элементов, то его внутреннее сопротивление r 0 равно нулю. Такой источник является идеальным.
На практике обычно приходится иметь дело с реальными источниками ЭДС, обладающими некоторым внутренним сопротивлением (рис. 1.7).
В таких источниках напряжение на зажимах зависит от тока в нагрузке.
Напряжение на зажимах реального источника в работающей цепи определяется соотношением
.
 |
Это выражение называют внешней характеристикой источника ЭДС.
 |
Анализируя внешнюю характеристику источника, можно сделать вывод, что напряжение на зажимах источника в режиме нагрузки всегда меньше ЭДС на величину падения напряжения на внутреннем сопротивлении источника. Зависимость напряжения от тока нагрузки показана на рис. 1.8 пунктирной линией. В свою очередь величина тока нагрузки зависит от сопротивления внешней цепи, поэтому можно считать, что напряжение на зажимах реального источника зависит от сопротивления внешней цепи.
В случае идеального источника внутренне сопротивление равно нулю. Напряжение на зажимах такого источника не зависит от тока нагрузки и равно ЭДС источника U = E. Зависимость напряжения от тока в идеальном источнике показана на рис. 1.8 сплошной линией.
Источники тока
Идеализированный источник тока – это активный элемент, ток которого не зависит от напряжения на его зажимах.
Считается, что внутреннее сопротивление идеального источника бесконечно велико, поэтому параметры внешней цепи не будут оказывать влияния на ток в источнике тока.
 |
На электрических схемах источник тока обозначается так, как показано на рис. 1.9.
Реальный источник тока обладает конечным внутренним сопротивлением или отличной от нуля проводимостью. Схема реального источника представлена на рис. 1.10.
Ток реального источника определяется разностью тока идеального источника J и внутреннего тока I 0:
,
где U – напряжение, приложенное к зажимам источника. Полученное выражение называют внешней характеристикой источника тока.
Зависимость тока источника от напряжения на его зажимах показано на рис. 1.11. В случае идеального источника внутренняя проводимость равна нулю и, исходя из уравнения внешней характеристики, можно заключить, что ток, идущий от источника равен току короткого замыкания источника. Эта зависимость показана на рис. 1.11 сплошной линией.
 |
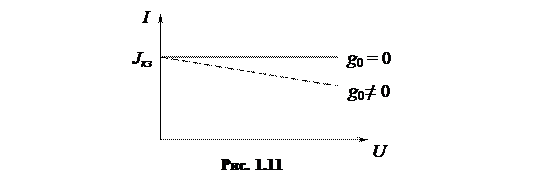В случае реального источника g 0 ≠ 0 и часть тока будет ответвляться через внутреннюю проводимость. Чем больше напряжение, приложенное к источнику, тем больший ток ответвляется и тем меньший ток поступает в нагрузку. Вольт-амперная характеристика реального источника показана на рис. 1.11 пунктирной линией.
Источник тока – это теоретическое понятие, но оно часто применяется для расчета электрических цепей. Примером источника тока может служить пентод.
Эквивалентное преобразование источников конечной мощности
Преобразование какого-либо участка цепи по отношению к внешним зажимам называют эквивалентным, если напряжение u и ток i на внешних зажимах при этом не изменяются.
Рассмотрим условие эквивалентности реальных источников напряжения и тока, представленных на рис. 1.12, а,б. Воспользуемся уравнением внешней характеристики источника ЭДС
.
Поделим почленно это уравнение на r 0
Здесь I – ток, протекающий через нагрузку;
– ток короткого замыкания источника ЭДС;
– ток, протекающий через внутреннее сопротивление.
Отсюда можно заключить, что 
или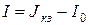 
, то есть получили внешнюю характеристику источника тока.
Следовательно, схему источника ЭДС можно заменить схемой источника тока при условии, что ток короткого замыкания источника и внутренняя проводимость определятся выражениями:
В свою очередь, схему источника тока можно заменить схемой источника ЭДС при условии, что внутреннее сопротивление и э.д.с. источника определятся выражениями:
Мощность источника ЭДС определяется произведением электродвижущей силы источника и тока в нагрузке
.
Мощность источника тока определяется произведением тока короткого замыкания и напряжения на зажимах источника:
.
