Несинусоидальные ЭДС, напряжения и токи
На практике э.д.с., напряжения и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников. В радиотехнике, вычислительной технике и т.п. применяются генераторы периодических несинусоидальных импульсов.
В общем случае характер изменения несинусоидальных величин может быть периодическим, почти периодическим и непериодическим. В данной лекции будут рассматриваться цепи только с несинусоидальными периодическими э.д.с., напряжениями и токами.
В качестве примера (рисунок 13.1,а) представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (рисунок 13.1,б).
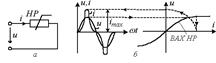
Рисунок 13.1
Разложение периодических несинусоидальных кривых в ряд Фурье
Периодическая функция 
где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд Фурье
 .
| (13.1) |
Здесь 
- постоянная составляющая или нулевая гармоника;
- первая (основная) гармоника, изменяющаяся с угловой частотой 
где Т – период несинусоидальной периодической функции.
В выражении (13.1) 
. Коэффициенты А0, аК и bK определяются по формулам
, 
, 
.
Свойства периодических кривых, обладающих симметрией:
Рисунок 13.2
а) кривые, симметричные относительно оси абсцисс.
К данному типу относятся кривые, удовлетворяющие равенству 
(рисунок 13. 2). В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е. 
;
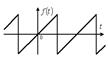
Рисунок 13.3 Рисунок 13.4
б) кривые, симметричные относительно оси ординат.
К данному типу относятся кривые, для которых выполняется равенство 
(рисунок 13.3). В их разложении отсутствуют синусные составляющие, т.е. 
;
в) кривые, симметричные относительно начала координат.
К этому типу относятся кривые, удовлетворяющие равенству 
(рисунок 13.4). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е. 
.
Действующее значение периодической несинусоидальной переменной. Действующее значение периодического тока
. (13.2)
Разложим периодический несинусоидальный ток в тригонометрический ряд
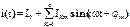и подставим в формулу (13.2), после преобразования получим 
. (13.3)
Аналогичные выражения имеют место для э.д.с. напряжения
, 
.
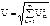