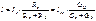Законы Кирхгофа. Закон Ома

Элементы электрической цепи (активные, пассивные)

Эл. цепью наз. совокупность устройств, предназначенных для прохождения тока

и описываемых с помощью понятий тока и напряжения

Пассивные элементы. Резистивным сопротивлением наз. идеализированный элемент,

обладающий только свойством необратимого рассеивания энергии.

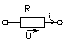
Количественной характеристикой: Сопротивление R Ом, проводимость (G=1/R, См)

Математическая модель, описывающая св-ва резистивного сопротивления,

определяется з-ном Ома: Ур-ие определяет зав-сть

напряжения от тока, наз. вольт-амперной х-кой (ВАХ).

Если R постоянно, то ВАХ линейна, если R зав-ит от напряжения и тока, то ВАX нелинейное

Мощность в резистивном сопротивлении:

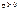
Индуктивным эл-ом наз. идеализированный эл-т эл. цепи,

обладающий только св-вом накопления им энергии магнитного поля.

Математическая модель, описывающая св-ва индуктивного элемента

определяется соотношением где - потокосцепление

Количественная х-ка: индуктивность(положитеьлное).

Если L=сonst, зав0ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная

мгновенная мощность: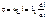

емкостным эл-от наз. идеализированный эл-т эл цепи,

обладающий только св-вом накапливать энергию эл поля.

Математическая модель, описывающая св-ва емкостного эл-та, опред-ся ВАХ: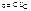

Количественная х-ка: емкость (С)(положительна)

Если С=сonst, зав-ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная

Мощность:

 

Активные эл-ты: завис-ые и незав-ые источники эл энергии

Независимым источником напряжения наз. идеализированный двухполюсный Эл-т,

напряжение на зажимах к-ого не зав-ит от протекающего через него тока.

Х-ся своим задающим напряжением U_г, или ЭДС е_г

ВАХ – прямая, параллельная оси токов

Независимым источником тока наз идеализированный двухполюсный эл-т,

ток к-ого не зав-ит от напряжения на его зажимах

Х-ся своим заданный током i_г

ВАх- прямая, параллельная оси напряжения

Зависимый источник - четырехполюсный эл-т с 2-мя парами зажимов- входных и выходных

Зависимые источники: источник напряжения, управляемый напряжением; источник тока,

управляемый напряжением; источник напряжения, управляемый током; источник тока, управляемый током.

Законы Кирхгофа. Закон Ома

1-ый з-н Кирхгофа (з-н токов): алгебраическая сумма токов ветвей, сходящихся в одном узле эл цепи,

равна нулю , где m число ветвей, сходящихся в узле

Число независимых ур-ий =n_у-1

2-ой з-н Кирхгофа (з-н напряжений): алгебраическая сумма напряжений ветвей

в любом контуре равна нулю

2-ой з-н Кирхгофа: (для падении янапряжений):

алгебраическая сумма падений напряжений на Эл-ах в замкнутом

контуре= алгебраической сумме ЭДС, действующих в данном контуре:

Число Ур-ий = n_в-n_у+1-n_ит

З-н Ома: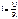

 

 

Преобразование эл схем

Последовательное соединение эл-ов: через эл-ты протекает один и тот же ток

Напряжение приложенной ко всей цепи

Для послед-ых соединений резистивных Эл-ов

Для послед-ых соединенй индуктивных Эл-ов

Для послед-ых соединенй емкостных Эл-ов

Параллельное соединение элементов: к Эл-м приложено одно и

то же напряжение Для параллельго соед-ия резиствных эл-ов:

Для параллельго соед-ия емкостных эл-ов:

Для параллельго соед-ия резиствных эл-ов:

 

Преобразование источника напряжения с параметрами U_г и R_г

в эквивалентный источник I_г G_г, или наоборот:

Принцип наложения

Принцип наложения: Реакция линейной цепи на сумму воздействий равна сумме реакций

от каждого воздействия в отдельности.

Напряжения и токи источников – воздействия, а напряжения и токи на эл-ах – реакции

Исп-ся: для нахождения р-ции в линейной цепи, находящейся как

под воздействием неск-их источников, так и при сложном произвольном воздействии одного источника

Линейная цепь с нес-кими источниками: результирующая р-ция в соотв-ии с принципом наложения

где n – общее число источников

Если в лин цепи приложено напряжение сложной формы,

применение принципа наложения позволяет после разложения этого воздействия на сумму

простейших найти р-цию цепи на каждое из них в отдельности с последующим наложением рез-ов

МКТ

Основан на 2-ом з-не Кирхгофа.

МКТ позволяет снизить число решаемых уравнений до числа независимых контуров,

определяемых равенством = n_в-n_у+1-n_ит

Каноническая форму записи ур-ий по МКТ: если цепь содержит к- независимых контуров:

- собственные сопротивления

МУП

Основывается на 1-ом з-не Кирхгофа и з-не Ома

Число ур-ий n_у-1

 

Метод двух узлов

 

Для цепей, имеющих только два узла 1 и 2.

План анализа:

1. Произвольно выбрать направления всех токов в ветвях на исходной схеме.

2. Вычислить узловое напряжение, направленное от узла 1 к узлу 2.

 

МЭГ

В соответствие с т Тевенина и Нортона задающее напряжение генератора

определяется как напряжение хх на разомкнутых зажимах активного

2-х-полюсника U_г=U_хх, а задающий ток- как ток кз I_г=I_кз.

внутреннее R активного 2-х-полюсника или его проводимость G_г

находятся как эквивалентные входные сопротивления или проводимость

отн-но разомкнутых зажимов пассивного 2-х-полюсника,

к-ый получается после исключения из схемы всех источников напряжения и тока.

При этом идеальные источники напряжения закорачиваются,

а токи- размыкаются; реальные источники

заменяются своими внутренними сопротивлениями или проводимостями.

или