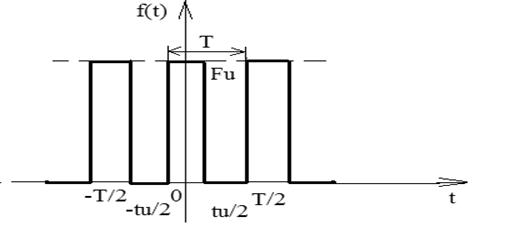
, где 
- скважность последовательности импульсов. Получается функция вида 
. Если рассматривать импульсы напряжения величиной Uu, то получим
, A0=2Uu/N.
Найдем нулевые точки синуса: 
,
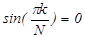
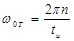Первая нулевая точка – самая важная для спектра последовательности прямоугольных импульсов.
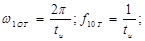постоянная составляющая 
.
АЧС последовательности прямоугольных импульсов при N=5:
ω1 ω2 2π/tu 4π/tu
(1/ tu) (f)
Основную долю энергии несут гармоники, расположенные от 0 до первой нулевой точки (около 90% энергии). Эту область частот, где сосредоточено 90% энергии сигнала, называют шириной (частотного) спектра сигнала.
Для последовательности прямоугольных импульсов ширина спектра → [0 
−1/tu] (Гц).
Любая цифровая передача сигнала требует большего спектра, чем простая аналоговая, так как 1/ tu >1/T.
ФЧС последовательности прямоугольных импульсов:
π
если sin(m)>0, то Ψk =0,
если sin(m)<0, то Ψk = π
Влияние длительности импульса и периода на вид спектра
Если длительность импульса уменьшается, то основная частота не изменится, нулевые точки переместятся вправо. До первой нулевой точки, где сосредоточена основная энергия, попадает больше составляющих. Технически отмечают, что спектр расширяется.
Если же длительность импульса возрастает, то происходит сужение спектра.
Если период повторения увеличивается, то уменьшается основная частота. Если период повторения уменьшается, то основная частота увеличивается.
Изменение положения импульса или начала отсчета
Это не влияет на АЧС, при этом изменяется только фазовый спектр. Это можно отразить на основе теоремы запаздывания:
Смещенная на tu /2 последовательность прямоугольных импульсов N=4
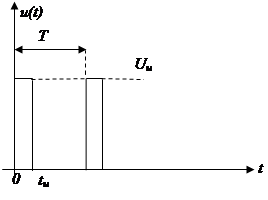Фазовый спектр для смещенного сигнала:
5.5.Понятие о расчете цепей при периодических сигналах
Методика расчета:
Определяется комплексный спектр периодического сигнала;
2. Оценивается спектр, оставляют наиболее значащие гармоники (первый критерий: отсекаются все, который составляют менее 0,1 от максимальной по величине амплитуды гармоники);
Рассчитываются токи и напряжения от каждой составляющей в отдельности. Можно использовать комплексный метод расчета.
Рассмотрим RLC - цепь с составляющими напряжения
Тогда i=I0+i1+i2+…..
I0=0 
аналогично 
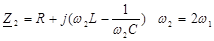
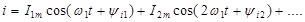
Можно определять комплексный спектр на выходе цепи через комплексный коэффициент передачи.
Оценить негармоническую функцию можно по действующему значению, т.е. среднеквадратичному за период:
Далее показан пример спектра на выходе подобной цепи при подаче на вход последовательности прямоугольных импульсов.
