Т.е. 
, где F1(p) – полином числителя, F2(p) – полином знаменателя.
Такую функцию можно разложить на элементарные дроби следующим образом:
. Здесь рК - корни знаменателя.
Тогда оригинал легко ищется в виде суммы экспонент: 
. Причем коэффициенты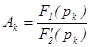 
. Разложение возможно, если старшая степень числителя меньше степени знаменателя.
Если один из корней равен 0, то 
Рассмотрим пример: 
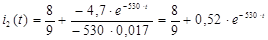
Корни могут быть комплексно-сопряженными. В этом случае пользуются общей формулой, причем 
, если 
. Здесь Mk - это модуль, а ψk - аргумент А k.
Можно использовать программные средства ЭВМ (Mathcad).
Операторные передаточные функции в теории цепей
Операторная передаточная функция представляет собой отношение операторного изображения реакции электрической цепи к операторному изображению воздействия на цепь. Техническое название - операторные коэффициенты передачи.
В зависимости от вида воздействия и типа реакции различают четыре варианта коэффициентов передач:
· по напряжению: 
· по току: 
· по сопротивлению: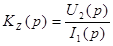 
· по проводимости: 
Передаточные функции по напряжению и току безразмерные, а по проводимости и сопротивлению имеют размерность См и Ом. Передаточные функции обычно определяются при нулевых независимых начальных условиях и используются для линейных цепей, где соблюдается коэффициент пропорциональности. Методика расчета основана на применении операторного метода, при этом воздействие рассматривается в общем виде, не конкретизируется, но может и конкретизироваться.
Рассмотрим следующий пример:
Определим операторный коэффициент передачи по напряжению. Для этого составляем операторную схему замещения при нулевых условиях:
Можно взять U1(p)=1/p. Получаем: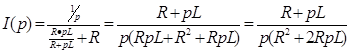 
Если есть операторные передаточные функции, то от них модно перейти к комплексным передаточным функциям, заменив p на jω, а затем определить амплитудно-частотную характеристику цепи (АЧХ), как модуль комплексной передаточной функции, и фазо частотную характеристику (ФЧХ), как аргумент комплексной функции.
АЧХ показывает, как изменяется отношение амплитуды выходного сигнала цепи к амплитуде входного при изменении частоты гармонического воздействия на цепь. ФЧХ показывает, как изменяется разность фаз выходного и входного сигнала при изменении частоты гармонического воздействия на цепь.
Рассмотри пример:
Для цепи рассмотренной ранее, где в Z1 индуктивность, а в Z2 такая же индуктивность и последовательно резистор получаем:
- АЧХ
- ФЧХ.
H(0)=1, H(∞)=0,5, φ(0)=0, φ(∞)=0, но в промежутке φ<0.
