Для того чтобы была возможность аналитически рассчитывать цепи с нелинейными элементами, необходимо иметь математические выражения для характеристик элементов. Сами эти характеристики обычно являются экспериментальными, т.е. полученными в результате измерений соответствующих элементов, а затем приводятся как справочные (типовые) данные. Процедуру математического описания некоторой заданной функции в математике называют аппроксимацией этой функции. Существует целый ряд типов аппроксимации: по выбранным точкам, по Тейлору, по Чебышеву и др. В конечном итоге необходимо получить математическое выражение, которое с какими-то заданными требованиями удовлетворяло исходной, аппроксимирующей функции. Для этого применяют полиномы: степенные, экспоненциальные и тригонометрические.
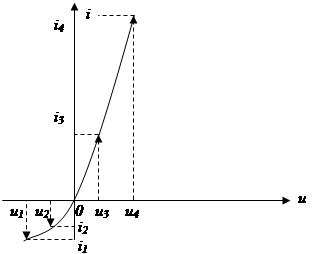Рассмотрим простейший способ: метод выбранных точек или узлов интерполяции степенным полиномом.
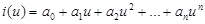
Необходимо определить коэффициенты полинома. Для этого выбирается (n+1) точка для заданной функции и составляется система уравнений:
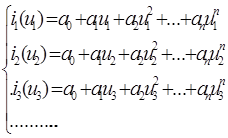
Из решения этой системы находятся коэффициенты а0, а1, а2, …, аn.
В выбранных точках аппроксимирующая функция будет совпадать с исходной, в других точках – отличаться (сильно или нет – зависит от степенного полинома, чем больше степень, тем меньше отклонение).
Можно использовать экспоненциальный полином:,
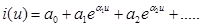
Второй метод: метод аппроксимации по Тейлору. В этом случае выбирается одна точка, где будет совпадение исходной функции с аппроксимирующей, но дополнительно ставится условие, чтобы в этой точке совпадали еще и производные.
Аппроксимация по Батерворту: это частный случай тейлоровской - выбирается простейший полином: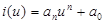 
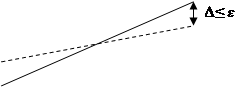
В этом случае можно определить максимальное отклонение ∆ и добиться, что бы оно было меньше заданной величины ε.
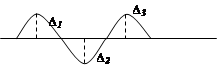Аппроксимация по Чебышеву является тоже степенной, там устанавливается совпадение в нескольких точках и минимизируется максимальное отклонение аппроксимирующей функции от исходной.
Чебышев установил, что все отклонения должны быть одинаковы для минимизации старшей степени полинома:
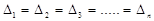
В инженерной практике используется еще так называемая кусочно-линейная аппроксимация – это описание заданной кривой отрезками прямых линий, например тремя.
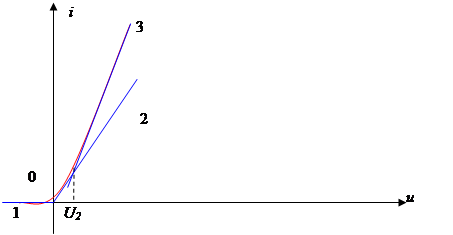
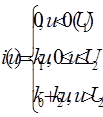
6.4. Определение реакции нелинейного элемента на гармоническое воздействие
1. Рассмотрим гармоническое воздействие малой амплитуды c постоянной составляющей
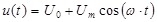, где 
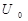- постоянная составляющая,
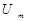- амплитуда малой величины, так что напряжение попадает на практически линейный участок.
В этом случае можно отдельно рассмотреть реакцию на постоянную составляющую - это будет постоянная величина, и на гармоническое воздействие - это будет гармоническая функция. Здесь можно использовать понятие статического и дифференциального сопротивлений, а также графический метод построения реакции путем переноса точек временной функции с использованием вольтамперной характеристики – ВАХ (АВХ). Ток получается примерно гармоническим.
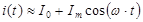, где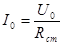 
, 
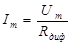в точке ВАХ со смещением U0.
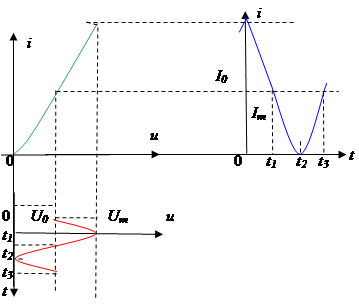2. Большая амплитуда напряжения
Напряжение попадает на существенно нелинейный участок характеристики. Используется графический метод (строится реакция путем переноса точек, здесь U0 <0). Ток получается явно не гармоническим.
 |
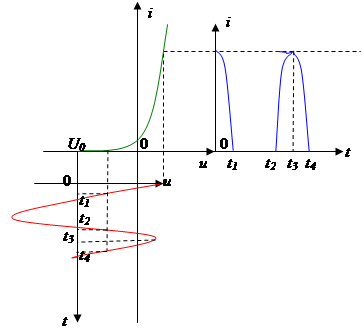
