6) Моделирование на ЭВМ.
Импульсная характеристика, методики расчета
Импульсная характеристика – это функция времени, численно равная реакции электрической цепи на единичное (по площади) импульсное воздействие; определяется для линейных цепей при нулевых независимых начальных условиях.
Имеется четыре типа импульсных характеристик: по напряжению, по току, по проводимости, по сопротивлению.
Размерность импульсной характеристики определяется отношением размерности реакции к размерности площади воздействия. Эти характеристики всегда имеют размерность, например характеристика по напряжению имеет размерность с-1.
Обозначение импульсной характеристики: 
. Рассматривают и запаздывающие импульсные характеристики 
.
Методики расчета:
1) Классический метод не подходит, так как воздействие равно ∞ или 0.
2) Операторный метод можно использовать с учетом, что операторное изображение воздействия равно 1.
3) Через операторный коэффициент передачи: импульсная характеристика соответствует оригиналу от операторного коэффициента передачи
Т(р)=K(p)Þ .
4) Через переходную характеристику: основано на том, что в линейных цепях реакция производной есть производная реакции.
Если h(0)=0, то с учетом 
Пример нахождения временных характеристик
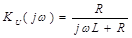
. Проверка К(0)= 1, по схеме при ω=0 индуктивность перемычка (ωL =0)и то же 1, при ω=∞ К(∞)= 0, индуктивность разрыв и то же получается 0 (сигнал на выход не проходит).
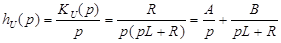Определив коэффициенты A и B,
получаем: 
Тогда: 
Проверка: при t =0 hU (0) = 0 и по схеме то же 0 (индуктивность - разрыв), hU (∞)=1 и по схеме 1 (индуктивность – перемычка). Найдем импульсную характеристику через производную переходной
Реакция цепи на сложное кусочно-непрерывное воздействие. Интегралы Дюамеля и наложения
Общие понятия
Рассмотрим следующую задачу: на вход цепи полается сложное воздействие x(t), необходимо определить реакцию цепи y(t).
Существует два способа решения подобных задач:
Способ
Можно сложную функцию разбить на сумму простых, например, на элементарные ступеньки, т.е.: 
,
х (0) – начальная ступенька, Δτ - промежуток времени между ступеньками, Δ xK – приращение х иего можно выразить через производную по вспомогательной переменной τ 
Тогда реакция цепи может быть найдена приблизительно как сумма реакций на отдельные ступенчатые воздействия с использованием переходной характеристики.
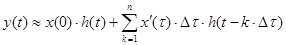Здесь сначала находится реакция на начальный скачок, а затем используется запаздывающая на k∙Δτ переходная характеристика. Чтобы точно найти реакцию, надо устремить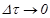 
Тогда сумма перейдет в интеграл: 
, где t – момент наблюдения.
Эта формула получила название интеграла Дюамеля (один из вариантов). Этой формулой удобно пользоваться, особенно если x(t) – линейная функция, так как производная при этом постоянна.
Способ
