Изображение производной и интеграла по времени
Используя эти свойства можно от интегральных и дифференциальных уравнений перейти к алгебраическим.
В ТЦ рассматривают основные законы но переводят их в операторную форму, для так называемых операторных схем замещения электрической цепи.
Законы Кирхгофа в операторной форме
Поскольку интегрирование – функция линейная и сумма интегралов соответствует интегралу суммы, то формально законы Кирхгофа можно записывать в операторном виде для операторных токов и напряжений, аналогично комплексной форме.
Рассмотрим 1 закон Кирхгофа
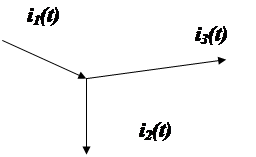
i1(t)-i2(t)-i3(t)=0 
I1(p)-I2(p)-I3(p)=0
Для напряжений аналогично.
U1(p)+U2(p)…..= 0
При записи может использоваться E(p) – операторная ЭДС или операторное изображение ЭДС.
Операторные схемы замещения реактивных элементов ЭЦ
1) Индуктивный элемент
Из математики известно, что 
В этом случае: UL(p)=L∙(p∙IL(p)-iL(0))=pL∙IL(p)-L∙iL(0).
Здесь pL=ZL(p) –можно представить как операторное сопротивление индуктивности. Второе слагаемое отражает начальные условия или запасы энергии в индуктивности.
Таким образом, операторная схема замещения индуктивного элемента выглядит следующим образом:
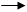
2) Емкостной элемент
Из математики известно, что 
. Тогда для данного случая получаем: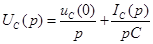 
. Здесь первое слагаемое отражает начальные условия или запасы энергии в емкости, а 1/pC= ZC(p) - операторное сопротивление емкости.
Таким образом, операторная схема замещения емкостного элемента выглядит следующим образом:
Закон Ома в операторном виде выполняется для резистора всегда
IR(p)=UR(p)/R, а для индуктивных и емкостных элементов только при нулевых начальных условиях.
После составления операторной схемы замещения цепи к ней можно применять любые методы расчета в операторной форме: МТВ, МКТ, МУН и др.
Применение операторного метода к параллельной LC-цепи
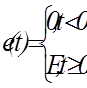Здесь включаемый источник эдс и нулевые независимые начальные условия.
В полученной схеме можно рассчитать любой операторный ток.
Сделаем проверку. Должны выполняться следующие условия: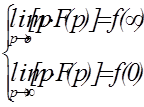 
. В данном случае 
. Произведя проверку, получаем тождество. Следовательно, решение верное. Но теперь необходимо найти ток, как функцию времени. Этому будут посвящены следующие темы.
Нахождение функции времени в операторном методе
Технически это значит нахождение откликов или реакций электрической цепи при каких-то коммутациях, т.е. зависимости токов или напряжений в электрических цепях. В общем, это математическая процедура нахождения оригинала по операторному изображению.
Теоретически можно выделить три способа:
· по обратному преобразованию Лапласа.
· табличным способом – подгонка операторного изображения под какие-то стандартные табличные функции.
| Оригинал | Изображение |
| |
| 
|
| 
|
| 
|
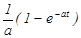
| sin(ω∙t) | 
|
| cos(ω∙t) | 
|
· применение теоремы разложения Хевисайда.
При определении операторных токов и напряжений в RLC -цепях можно увидеть, что они представляют собой дробно-рациональные функции сложного вида.
