Считается, что энергия не может изменяться скачком, т.е. мгновенно – это касается энергоемких элементов (L и C). На этой основе установлено два закона коммутации.
Математически первый закон коммутации запишется в виде формулы:
yS (0-) = yS (0) = yS (0+)
Суммарное потокосцепление индуктивных элементов в цепи не может изменяться скачком в момент коммутации и является непрерывной функцией времени. Непосредственно после коммутации оно равно значению в момент коммутации и значению непосредственно перед коммутацией (предел справа равен пределу слева).

Частный случай: если индуктивные элементы в момент коммутации не меняют свои параметры, то закон коммутации будет справедлив для токов индуктивных элементов, поскольку потокосцепление
yк(t) = Lк·iк(t), Lк = const, iLк(0-) = iLк(0) = iLк(0+).
Практическая формулировка: если индуктивность не меняется в момент коммутации, то ток в индуктивном элементе не изменяется скачком и в момент коммутации равен току в индуктивности непосредственно перед коммутацией.
Математическая запись второго закона коммутации имеет вид:
qS (0-) = qS (0) = qS (0+)
Частный случай: если емкость не меняется в момент коммутации, то закон действителен для емкостного напряжения qк = Cк·uк,
Cк = const, uCк(0-) = uCк(0) = uCк(0+).
Практическая формулировка: если емкость не меняется в момент коммутации, то напряжение на емкостном элементе не изменяется скачком и в момент коммутации равно напряжению на емкости непосредственно перед коммутацией
Физическое обоснование этих законов обусловлено невозможностью получения бесконечно больших величин. Если, например, ток (потокосцепление) в индуктивности изменится скачком, то скачком должна измениться и энергия индуктивности, что приводит к бесконечно большому напряжению  и мощности, поскольку мощность это производная энергии. Аналогично и для емкостного напряжения (заряда),
и мощности, поскольку мощность это производная энергии. Аналогично и для емкостного напряжения (заряда),
поскольку  .
.
Начальные и конечные условия
Одной из основных задач в расчетах переходных процессов является определение начальных условий, что делается на основе законов теории цепей. Начальными условиями называются значения электрических величин в начальный момент времени t =0 (в момент коммутации). Начальные условия при переходных процессах разделяют на независимые (связаны с законами коммутации) и зависимые (все остальные). Независимые условия – токи в индуктивных элементах iL(0) и напряжения на емкостных элементах uC(0) в момент коммутации (при условии, что L и C – const они не изменяются скачком).

Аналогично для емкости 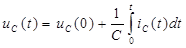
Значения величин после окончания переходного процесса (t ®¥) называются конечными условиями или установившимися значениями. Они могут быть постоянными или периодическими.
При определении начальных и конечных условий удобно пользоваться схемами замещения элементов в различные моменты времени.
Схемы замещения элементов в различные моменты времени
Источники энергии: они представляются соответственно источниками тока и напряжения с учетом их зависимости от времени до и после коммутации.
Резисторы: если они безинерционные, так резисторами и остаются с учетом их изменения во времени. Реактивные: элементы (индуктивности и емкости) имеют специфические схемы замещения.
| t Элементы | t=0- | t=0 | t=∞ | |||||||||
 Индуктивность Индуктивность

   
| В зависимости от источника, действующего в цепи:
1) нет источников – неопределенная ситуация;
2) ист. постоянного действия → перемычка (к.з.)
 3) источник гармонического действия - сопротивление
3) источник гармонического действия - сопротивление
| При любых источниках есть два варианта:
1) нулевые нач. условия (iL(0-)=0). т.е. нет запаса энергии, то iL(0)=0 → разрыв
(х.х.)
→источник тока | В зависимости от источника | |||||||||
Емкость
 
| В зависимости от источника, действующего в цепи (по принципу дуальности):
1) нет источников – неопределенная ситуация;
2) ист. постоянного действия → разрыв (х.х.)
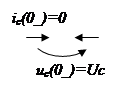 3) источник гармонического действия → сопротивление
3) источник гармонического действия → сопротивление

| При любых источниках есть два варианта:
1) нулевые нач. условия uC(0-)=0 т.е. нет запаса энергии, то uC(0)=0 → перемычка (к.з.)
iC(0)=?
2) Ненулевые нач. условия uC(0-)≠0 → источник напряжения
|
В общем случае до и после коммутации схемы замещения могут быть разными (до коммутации мог быть один источник подключен, а после другой).
Классический метод анализа переходных процессов
в электрических цепях
Классический метод расчета переходных процессов основан на непосредственном решении системы дифференциальных уравнений, составленных для электрической цепи на основе законов Кирхгофа. В этом случае переходные токи и напряжения ищутся в виде двух составляющих: свободной и установившейся или принужденной

Установившаяся (принужденная) составляющая является частным решением неоднородного уравнения или системы и определяется (устанавливается) действующими источниками (постоянного, переменного или периодического действия). Свободная составляющая соответствует поведению цепи в свободном режиме, без источников и соответствует математически общему решению однородного дифференциального уравнения или системы, и ищется как сумма экспонент:
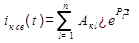 ,
,
где Pl – (показатели экспонент) корни характеристического уравнения, соответствующего дифференциальному (они одинаковы для всех величин токов и напряжений цепи и их количество определяется старшей степенью уравнения), а Aкl - множители, определяемые с применением начальных и конечных условий (они разные).
1.2. Переходные процессы в электрических цепях первого порядка.
Анализ процессов в последовательных RL и RC цепях
Рассмотрим подключение источника постоянного напряжения e(t)=E.
| RL | RC |
|    
|
| 1. Определение начальных условий | |
 (первый закон коммутации – источник отключен) (первый закон коммутации – источник отключен)
|  (второй закон коммутации– источник отключен) (второй закон коммутации– источник отключен)
|
2. Уравнения в момент времени  (источник постоянный подключен) (источник постоянный подключен)
| |


| 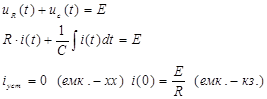
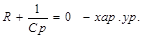
 
|
| 3. Используя начальные условия, получаем: | |


| 
|
| 4. Проверка решения | |

| 
|
| 5. Построение графиков – по формулам, изменяя t | |
 
|  
|
Понятие о длительности переходного процесса и постоянной времени
Теоретически переходной процесс длится бесконечно долго. На практике его ограничивают моментом, когда процесс заканчивается на 95% - 99% (остается 5–1%).
Еще используют понятие постоянной времени – это такой промежуток времени, в течение которого свободная (экспоненциальная) составляющая уменьшается по величине в e раз (2,72).
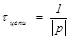 , где p – показатель экспоненты.
, где p – показатель экспоненты.
Для последовательных RL и RC цепочек постоянная времени равна соответственно:  ;
;  .
.
Чем больше τ, тем медленнее идет переходной процесс и дольше длится. За время 2τ свободная составляющая уменьшится в e2≈ 7 раз, за 3τ – в e3≈ 20 раз и остается 5%, за 5τ в >100 раз и остается менее 1% от свободной составляющей.Если есть несколько корней уравнения, то берется максимальное τ. Таким образом, за длительность переходного процесса принимают время равное 3-5 τ. Формулы для переходных токов и напряжений можно записывать с использованием τ.
Отключение источника
| RL | RC |
  
|    
|
| Получаем ненулевые начальные условия | |

| 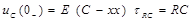
|
| Конечные условия | |

| 
|
| Уравнения такие же, только правая часть равна 0 | |
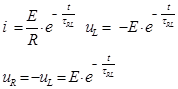
| 
|
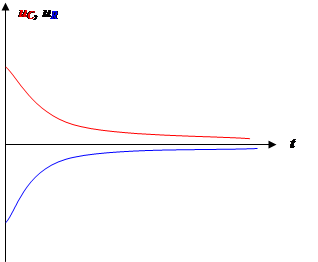
| Графики | |
  
|   
|
Если не было скачка при включении какой-то величины, то не будет и при выключении. Если был скачок при включении, то точно такой же, но в обратную сторону будет скачок при выключении. Это следствие из закона сохранения энергии справедливо, если в цепи ничего не меняется.
Определение τ для сложной цепи с одним реактивным элементом и несколькими резисторами
В этом случае постоянную времени ищут, используя следующую формулу:  для цепи с емкостным элементом и
для цепи с емкостным элементом и  для цепи с индуктивным элементом, где RЭ – эквивалентное (общее) сопротивление, которое определяют относительно реактивного элемента после срабатывания ключа.
для цепи с индуктивным элементом, где RЭ – эквивалентное (общее) сопротивление, которое определяют относительно реактивного элемента после срабатывания ключа.
Рассмотрим следующий пример:
В данном случае источник эдс (напряжения) рассматривается как перемычка  при подключении источника, а при выключении перемычка получается за счет срабатывания ключа. В обоих случаях
при подключении источника, а при выключении перемычка получается за счет срабатывания ключа. В обоих случаях

 ,
, 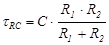
Подключение источника гармонического напряжения

 e(t)=Emcos(ωt+ΨE)
e(t)=Emcos(ωt+ΨE)
Дифференциальное и характеристическое уравнения такие же, как и для цепи с источником постоянного напряжения, значит и показатель экспоненты такой же. Будет отличаться принужденная (установившаяся) составляющая: она будет гармонической:



Подставив начальные условия (t=0), получим с учетом i (0)=0 значение множителя A:

Множитель A может получаться разным: от 0 (Ψi =π/2) до некоторого максимального значения (Ψi =0). Ψi = ΨЕ - φ, а угол ΨЕ зависит от момента коммутации. Следовательно множитель А получается тоже зависящим на практике от момента коммутации (теоретически от выбранного начала отсчета в косинусоиде).
Рассмотрим график тока, состоящий из двух составляющих –






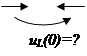
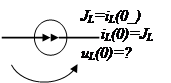 2) ненулевые нач. условия iL(0-)≠0
2) ненулевые нач. условия iL(0-)≠0



