Знайти силу, з якою вода тисне на пластину, переріз якої має форму рівнобічної трапеції (рис. 20).
15.1. a = 4,5 м; b = 6,6 м; h = 3,0 м.
15.2. a = 4,8 м; b = 7,2 м; h = 3,0 м.
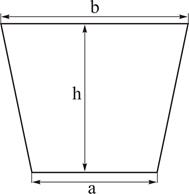Рис. 20
|
15.3. a = 5,1 м; b = 7,8 м; h = 3,0 м.
15.4. a = 5,4 м; b = 8,4 м; h = 3,0 м.
15.5. a = 5,7 м; b = 9,0 м; h = 4,0 м.
15.6. a = 6,0 м; b = 9,6 м; h = 4,0 м.
15.7. a = 6,3 м; b = 10,8 м; h = 4,0 м.
15.8. a = 6,6 м; b = 10,8 м; h = 5,0 м.
15.9. a = 6,9 м; b = 11,4 м; h = 5,0 м.
15.10. a = 7,2 м; b = 12,0 м; h = 5,0 м.
15.11. a = 7,5 м; b = 12,5 м; h = 5,0 м.
15.12. a = 7,8 м; b = 13 м; h = 6,0 м.
15.13. a = 8 м; b = 13,2 м; h = 6,0 м.
15.14. a = 8,1 м; b = 13,4 м; h = 6,0 м.
15.15. a = 8,3 м; b = 13,5 м; h = 7,0 м.
Задача 15.3 Обчислити роботу змінної сили, при цьому використовуючи формулу
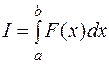, (20)
де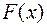 
- змінна сила, що діє на відрізку 
.
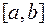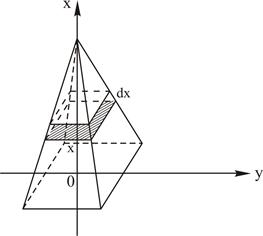Рис. 21
|
Приклад 15.3 Обчислити роботу, яку потрібно витратити для побудови піраміди з квадратною основою, якщо висота піраміди h, сторона основи а, питома вага матеріалу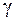 
.
Розв'язання. Розташуємо осі координат як показано на рис. 21. Для підйому на висоту х будівельного матеріалу об’ємом 
- буде витрачена робота 
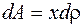, де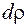 
- вага об’єму , рівна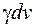 
. Отже, 
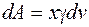. Оскільки об’єм (рис. 21) має малу товщину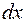 
, то можна вважати, що він являє собою прямокутний паралелепіпед з квадратною основою і висотою 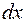. Звідси 
.
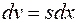Знайдемо S. З геометрії відомо, що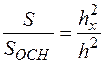 
.
Звідси 
і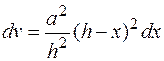 
;
.
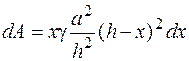Повна робота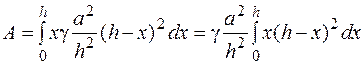 
.
Остаточно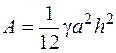 
(од. роб.)
Знайти роботу, яку потрібно витратити, щоб викопати котлован циліндричної форми радіуса R і висоти H, якщо питома вага породи g.
15.16. R =10 м, H =5,4 м.
15.17. R =8,2 м, H =6 м.
15.18. R =8,4 м, H =6,3 м.
15.19. R =8,9 м, H =4,5 м.
15.20. R =12 м, H =4,8 м.
15.21. R =10,5 м, H =7,8 м.
15.22. R =15,2 м, H =6,2 м.
15.23. R =15,8 м, H =5,8 м.
15.24. R =14,5 м, H =3,3 м.
15.25. R =12,8 м, H =7,4 м.
15.26. R =12,4 м, H =10 м.
15.27. R =10,3 м, H =8,5 м.
15.28. R =10,6 м, H =12,3 м.
15.29. R =15,4 м, H =5,7 м.
15.30. R =25,1 м, H =10,4 м.
ЛІТЕРАТУРА
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. 1, гл. Х, ХІ, ХІІ. – М.: Наука, 1978.
2. Бугров Я.С., Никольский С.С. Дифференциальное и интегральное исчисления, гл. V, VI, VII. – М.: Наука, 1980.
3. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1977.
4. Кузнецов Л.А. Сборник заданий по высшей математике. – М.: Высш. шк., 1983.
5. Дубовик В.П., Юрик І.І. Вища математика: Навчальний посібник.- К.: Вища шк., 1993.-648с.
6. Денисюк В.П., Репета В.К. Вища математика. Модульна технологія навчання: Навчальний посібник:У 4-х ч. –Ч. 2.-К.: Книжкове вид-во НАУ,2005.-276с.
Навчально-методичне видання
ІНТЕГРАЛи та їх застосування
Навчальний посібник з вищої математики для студентів 1 курсу будівельних спеціальностей
Укладачі: БОНДАРЕНКО Наталія В’ячеславівна
ЗАБАРИЛО Олексій Віталійович
Отрашевська Валентина Володимирівна
Пастухова Марина Семенівна
СОКОЛОВА Людмила Віталіївна
Підписано до друку 2008. Формат 60х801/16.
Папір офсетний. Гарнітура Таймс. Друк на різографі.
Ум. друк. арк. 1,39. Обл.-вид. арк. 1,5. Ум. фарбовід 13.
Тираж 100 прим. Вид. № Замовлення №
КНУБА, Повітрофлотський проспект, 31, Київ-680, 030680
Віддруковано в редакційно-видавничому відділі
Київського національного університету будівництва і архітектури
Свідоцтво про внесення до Державного реєстру суб’єктів
видавничої справи ДК № 808 від 13.02.2002 р.
