 , ,

| 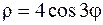 , ,

| 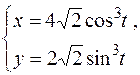
| |
 , ,
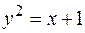
| 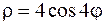
| 
| |
 , ,

| 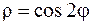
| 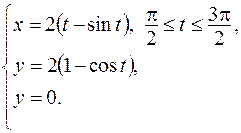
| |
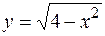 , ,

|  . .
| 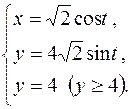
| |
 , ,

|  , ,

| 
| |
 , ,

| 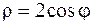 , ,
 . .
| 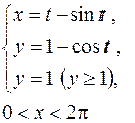
| |
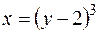 , ,
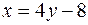
|  , ,

| 
| |
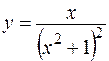 , ,

|  , ,
 . .
| 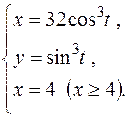
| |
 , ,
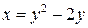
|  , ,

| 
| |
 , ,

| 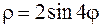
| 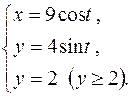
| |
 , ,
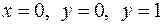
|  . .
| 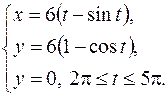
| |
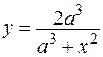 , , 
| 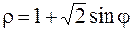 . .
| 
| |
 , ,
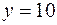
| 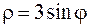 , ,
 . .
| 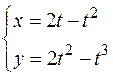
| |
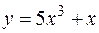 , ,
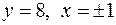
|  , ,
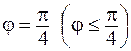 . .
| 
| |
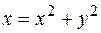 , ,

| 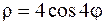
| 
| |
 , ,

| 
| 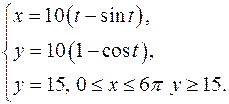
| |
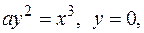 , ,

| 
| 
| |
 , ,
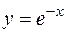
| 
| 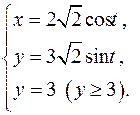
| |
 , ,
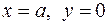 / /
| 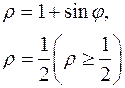
| 
| |
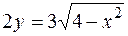 , ,
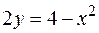
| 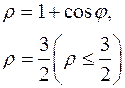
| 
| |
 , ,

| 
| 
| |
 , ,

| 
| 
| |
 , ,
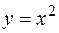
| 
| 
| |
 , ,
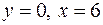
| 
| 
| |
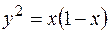 , ,
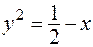
| 
| 
| |
 , ,

| 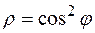
| 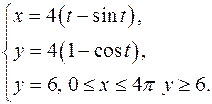
| |
 , ,

| 
| 
| |
 , ,

| 
| 
| |
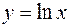 , ,
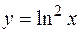
| 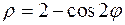
| 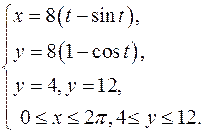
| |
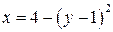

| 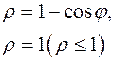
| 
|
Знаходження довжини плоскої кривої
Довжина дуги гладкої плоскої кривої, заданої рівнянням  на відрізку
на відрізку  , обчислюється за формулою
, обчислюється за формулою
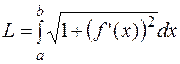 . (10)
. (10)
Якщо ж крива задана параметрично:
 ,
,  ,
,  ,
,
то
 . (11)
. (11)
Крива може бути задана в полярній системі координат:
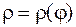 ,
, 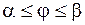 .
.
Тоді
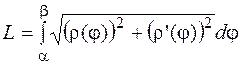 . (12)
. (12)
Задача 13. (13.1. а, б – 13.30. а, б.). Обчислити довжину дуги заданої плоскої кривої
Приклад 13.1 Знайти довжину дуги лінії кардіоїди, що задана рівнянням  ,
,  .
.
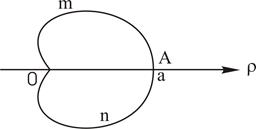 Рис. 11
Рис. 11
|
Розв'язання. Зробимо схематичний рисунок кардіоїди (рис. 11). З рисунок видно, що крива складається з двох симетричних частин, одна з яких (AmO) відповідає зміні кута  від 0 до
від 0 до  , друга – (O n A) – від
, друга – (O n A) – від 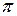 до
до  . Тому достатньо обчислити довжину половини дуги і подвоїти результат. Крива задана в полярній системі координат. Тому для розв’язання задачі потрібно використати формулу (12).
. Тому достатньо обчислити довжину половини дуги і подвоїти результат. Крива задана в полярній системі координат. Тому для розв’язання задачі потрібно використати формулу (12).
Спочатку знаходимо довжину дуги (AmO), що описується при зміні кута  від 0 до
від 0 до  :
:

Так як  при
при  , то
, то  і
і
 ,
, 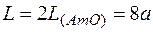 лін. од.
лін. од.
приклад 13.2. Обчислити довжину дуги напівкубічної параболи  , що вирізана параболою
, що вирізана параболою  .
.
Розв'язання. Зробимо схематичний рисунок (рис. 12) З рисунка видно, що в задачі потрібно знайти довжину дуги 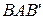 , що складається з двох симетричних частин. Тому достатньо обчислити довжину дуги АВ і подвоїти результат. Для знаходження меж інтегрування достатньо знайти абсцису точки В, оскільки абсциса точки А уже відома і рівна p. Розв’яжемо систему рівнянь двох парабол:
, що складається з двох симетричних частин. Тому достатньо обчислити довжину дуги АВ і подвоїти результат. Для знаходження меж інтегрування достатньо знайти абсцису точки В, оскільки абсциса точки А уже відома і рівна p. Розв’яжемо систему рівнянь двох парабол:
 Рис. 12 Рис. 12
|
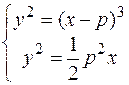

 .
.
Отримали кубічне рівняння, розв’язок якого знаходимо підбором:  .
.
Так як функцію можна записати рівнянням  , то для розв’язання задачі використовується формула (10), де
, то для розв’язання задачі використовується формула (10), де  ,
, 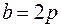 ,
,  ,
,  .
.

Зауваження. 1. якщо при обчисленні довжин дуг, межі інтегрування відомі, будувати рисунок не обов’язково.
2. В деяких випадках при використанні формули (10) доцільно в якості значення функції покласти змінну x і формула (10) матиме вигляд  , де дуга кривої буде задана рівнянням
, де дуга кривої буде задана рівнянням  ,
, 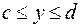 .
.
ЗАДАЧА 13. Індивідуальні завдання
 1. а) 1. а)   , ,  . .
| б) 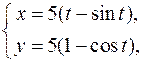  . .
|
2.а)  , ,  . .
| б)  , , 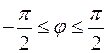 . .
|
3. а)  . .
| б)  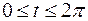
|
4 а)  , , 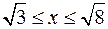 . .
| б)  , , 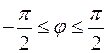
|
5. а)  , ,  . .
| б)  
|
6. а) 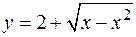 , , 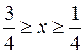 . .
| б) 
|
7.а) 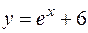 , , 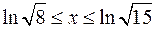 . .
| б) 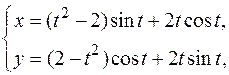  . .
|
8. а)  . .
| б) 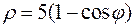 . .
|
9. а)  , ,  . .
| б) 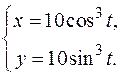
|
10. а) 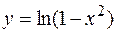 , , 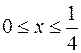 . .
| б)  . .
|
11. а) 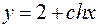 , ,  . .
| б) 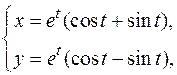 
|
12. а)  , ,  . .
| б)  , , 
|
13.а)  , , 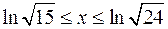 . .
| б) 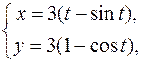  . .
|
14.а)  , ,  . .
| б) 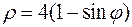 . .
|
15.а)  , ,  . .
| б) 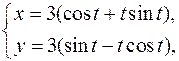 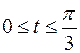 . .
|
16. а)  . .
| б) 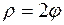 , ,  . .
|
17.а)  , ,  . .
| б) 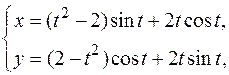 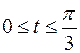 . .
|
18. а) 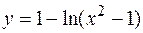 , , 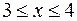 . .
| б)  . .
|
19.а) 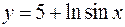 , ,  . .
| б) 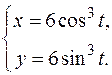 , , 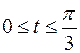 . .
|
20. а)  . .
| б)  , , 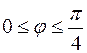 . .
|
21. а)  , ,  . .
| б) 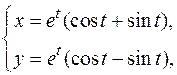  . .
|
22.а) 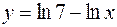 , , 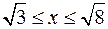 . .
| б)  , ,  . .
|
23. а)  , ,  . .
| б) 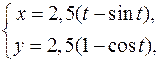  . .
|
24. а)  . .
| б) 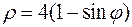 , ,  . .
|
25. а)  , , 
| б)   . .
|
26.а)  , ,  . .
| б)  , , 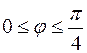 . .
|
27.а)  , , 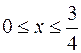 . .
| б)  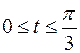 . .
|
28.а)  , , 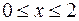 . .
| б)  , , 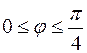
|
29.а)  , ,  . .
| б) 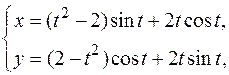 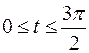 . .
|
30. а)  , , 
| б)  . .
|
Знаходження площ поверхонь та
Об’ємів тіл обертання
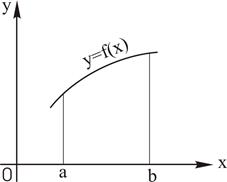
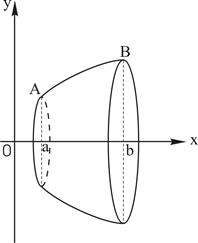
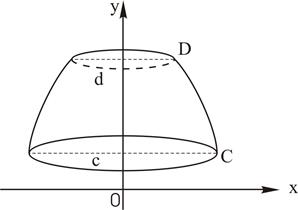
Нехай задана криволінійна трапеція (рис. 13), що спирається на вісь OX і обмежена неперервною кривою  . Обертаючи таку трапецію навколо осі ОХ, отримаємо тіло обертання, об’єм якого обчислюється за формулою
. Обертаючи таку трапецію навколо осі ОХ, отримаємо тіло обертання, об’єм якого обчислюється за формулою
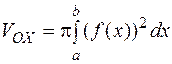 . (13)
. (13)
Якщо ж трапеція спирається на вісь OY (мал. 14) і обертається навколо осі OY, то об’єм тіла обертання обчислюється за формулою
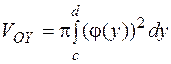 (14)
(14)
Зауваження 1. Якщо крива, що обмежує трапецію, задається n аналітичними виразами, то задана трапеція розбивається на n трапецій. Тоді обчислюють об’єм тіл, отриманих обертанням кожної з n трапецій, і результати сумують.
| 
|
| Рис. 13 | Рис. 14 |
Зауваження 2. Якщо тіло утворюється обертанням фігури, що не є трапецією (рис. 15), то воно розкладається на трапеції: знаходять об’єм тіл обертання кожної з побудованих трапецій. Тоді результуючий об’єм V=Vоб. А1 А m B B1 -. Vоб. А1 А n B B1.
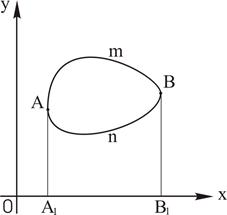 Рис. 15
Рис. 15
|
3. У випадку параметрично заданої кривої  ,
,  слід у формулах (13), (14) покласти
слід у формулах (13), (14) покласти  ,
,  ,
,  ,
,  і знайти відповідні межі зміни змінної t. Схема розв’язання задачі обчислення об’єма тіла обертання наступна:
і знайти відповідні межі зміни змінної t. Схема розв’язання задачі обчислення об’єма тіла обертання наступна:
1) виконати схематичний малюнок фігури, об’єм тіла обертання якої потрібно знайти;
2) знайти межі інтегрування (див. схему розв’язку задачі 9);
3) скласти, а потім і обчислити визначений інтеграл.

|
Задача 14. (14.1 – 14.30). Обчислити об’єм тіла обертання або площу поверхні тіла обертання.
Приклад 14.1 Обчислити об’єм тіла, утвореного обертанням навколо осі OX фігури, обмеженої напівеліпсом 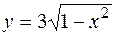 , напівпараболою
, напівпараболою  і віссю OY.
і віссю OY.
Розв'язання. Зробимо схематичний рисунок. Рівняння 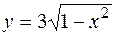 задає верхню пловину еліпса
задає верхню пловину еліпса  ; рівняння
; рівняння  задає праву вітку параболи
задає праву вітку параболи  з вершиною в точці (0,1), що перетинає вісь ОХ в точках (1,0), (-1,0). Навколо осі ОХ обертається заштрихована фігура АВС. Об’єм тіла обертання знайдемо як різницю об’ємів, отриманих від обертання трапецій ОВС та ОАС. Використаємо формулу (13):
з вершиною в точці (0,1), що перетинає вісь ОХ в точках (1,0), (-1,0). Навколо осі ОХ обертається заштрихована фігура АВС. Об’єм тіла обертання знайдемо як різницю об’ємів, отриманих від обертання трапецій ОВС та ОАС. Використаємо формулу (13):

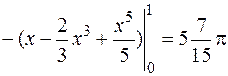 куб. од.
куб. од.
Якщо навколо осі координат обертається дуга кривої АВ (рис. 16, 17), то утворюється поверхня обертання, площа Р якої обчислюється за наступними формулами:
| 
|
| Рис. 16 | Рис. 17 |
крива задана явним рівнянням  і обертається навколо осі ОХ,
і обертається навколо осі ОХ,  :
:
 ; (15)
; (15)
крива задана параметрично  ,
,  ,
,  і обертається навколо осі ОХ:
і обертається навколо осі ОХ:
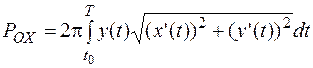 ; (16)
; (16)
крива задана явним рівнянням  і обертається навколо осі OY (рис. 17):
і обертається навколо осі OY (рис. 17):
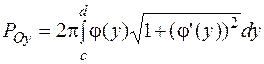 ; (17)
; (17)
крива задана параметрично  ,
,  ,
,  і обертається навколо осі OY:
і обертається навколо осі OY:
 . (18)
. (18)
Приклад 14.1 Знайти площу поверхні, утвореної обертанням астроїди  навколо осі ОХ.
навколо осі ОХ.
Розв'язання. Будуємо схематичний рисунок поверхні, утвореної обертанням астроїди в параметричній формі:
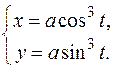

|
Астроїда симетрична відносно осей координат. Тому для розв'язання задачі достатньо обчислити площу поверхні, отриманої обертанням дуги АВ, що розміщення в першій четверті, і результат помножити на 2.
Розв’язання1. Для обчислення площі поверхні обертання астроїди навколо осі ОХ використаємо параметричне задання кривої, а отже, формулу (16). Так як дуга АВ описується при  , то
, то
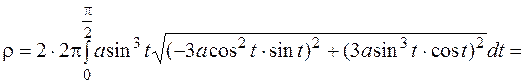
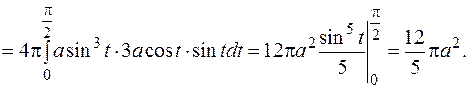
Шукана площа  (кв. од.).
(кв. од.).
Розв'язання.2. Для розв’язання використаємо початкове рівняння астроїди, а отже, формулу (15). З рівняння астроїди
 .
.
За формулою (15)
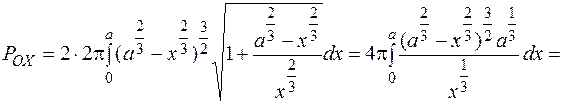
 (кв. од.)
(кв. од.)
Зауваження. Порівнюючи наведені два розв’язки, бачимо, що перший спосіб приводить до більш простих операцій обчислювального характеру. В деяких випадках перехід до параметричної форми задання кривої може значно спростити інтеграл, отриманий в результаті розв’язку задачі.






