Розділ I
Невизначений інтеграл
означення. функція F(x) називається первісною функції f(x) на проміжку I, якщо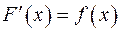 
для всіх 
.
Теорема. Якщо функція F(x) є первісною функції f(x) на проміжку I, то функція 
, де С – довільна стала, також буде первісною даної функції на I.
Правильним є й обернене твердження: кожну функцію, що є первісною функції f(x) на проміжку I, можна подати у вигляді 
, де С – довільна стала.
Операція знаходження для функції всіх її первісних називається інтегруванням функції і є оберненою операцією відносно диференціювання.
Вираз , де С – довільна стала, називається невизначеним інтегралом і позначається 
, тобто = . при цьому вираз 
називається підінтегральним виразом, а функція f(x) підінтегральною функцією.
отже для того, щоб знайти невизначений інтеграл від заданої функції f(x), потрібно знайти одну з первісних даної функції та додати до неї довільну сталу. правильність інтегрування перевіряють диференціюванням: 
.
Властивості невизначеного інтеграла
1. 
2. 
3. 
4. 
таблиця основних інтегралів
1. 
| 2.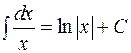 
|
3. 
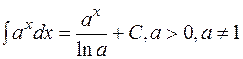
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
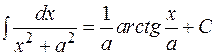
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
Розглянемо основні методи інтегрування.
ЗАДАЧА 1 (1.1-1.30). Знайти інтеграл безпосереднім інтегруванням.
Приклад 1.1 Знайти.
Розв'язання. Подамо даний інтеграл у вигляді суми табличних інтегралів: 
= 
= 
= 
= 
= 
Відповідь. 
ПРИКЛАД 1.2 Знайти 
.
Розв'язання. = 
= 
= 
= 
.
Відповідь.
ЗАДАЧА 1. Індивідуальні завдання
1. 
| 2.  
| 3. 
|
4. 
| 5. 
| 6.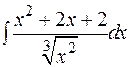 
|
7. 
| 8. 
| 9. 
|
10. 
| 11. 
| 12. 
|
13. 
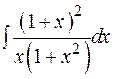
| 14. 
| 15. 
|
16. 
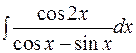
| 17. 
| 18. 
|
19. 
| 20. 
| 21. 
|
22. 
| 23. 
| 24. 
|
25. 
| 26. 
| 27. 
|
28. 
| 29. 
| 30.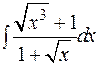 
|
Метод внесення функції під знак диференціала
метод внесення функції під знак диференціала доцільно застосовувати, якщо підінтегральний вираз можна подати у вигляді добутку деякої функції та її диференціала, тобто
.
наведемо деякі корисні співвідношення (таблиця диференціалів):
| 
| 
|
| 
| 
|
 , 
| 
| 
|
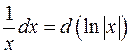
ЗАДАЧА 2 (2.1-2.30) Знайти невизначений інтеграл за допомогою метода введення функції під знак диференціала.
Приклад 2.1 знайти інтеграл 
.
Розв'язання. = 
=
= 
Відповідь.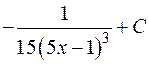 
приклад 2.2 Знайти інтеграл 
.
Розв'язання. Виділимо повний квадрат у виразі, що знаходиться у знаменнику підінтегрального виразу: 
. враховуючи, що 
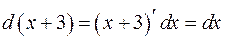, знаходимо інтеграл: = 
= 
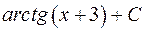
Відповідь.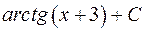
ЗАДАЧА 2. Індивідуальні завдання
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 
|
7. 
| 8. 
| 9. 
|
10. 
| 11.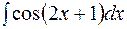 
| 12. 
|
13. 
| 14. 
| 15. 
|
16. 
| 17. 
| 18. 
|
19. 
| 20. 
| 21. 
|
22. 
| 23. 
| 24. 
|
25. 
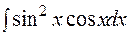
| 26. 
| 27. 
|
28. 
| 29. 
| 30. 
|
метод інтегрування частинами.
для знаходження інтегралів від добутку многочленів на трансцендентну функцію (1,2)
1. 
2. 
, а також інтегралів виду
3. 
та інш.
застосовують формулу 
, (1)
де 
- диференційовані функції. В інтегралах першого типу за u слід брати многочлен, а за 
ту частину підінтегрального виразу, що залишилась. В результаті інтеграл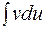 
має стати простішим порівняно з початковим. в інтегралах другого типу навпаки за u приймаємо логарифмічну чи обернену тригонометричну функції. в інтегралах третього типу отримуємо лінійне рівняння відносно початкового інтеграла.
задача 3 (3.1-3.30) знайти невизначений інтегралза допомогою методу інтегрування частинами.
приклад 3.1 знайти інтеграл 
.
Розв'язання. Покладаємо 
, тоді 
, 
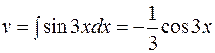. Згідно з формулою інтегрування частинами маємо: = 
+ 
= + 
.
Відповідь. +
приклад 3.2 знайти інтеграл 
.
Розв'язання. Покладаємо 
, 
, тоді 
, 
. застосувавши формулу інтегрування частинами, отримуємо: = 
= 
- 
. Інтеграл також знаходимо методом інтегрування частинами. Покладаємо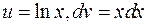 
, тоді 
, = 
- 
= - 
= - 
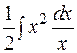+С.
остаточно маємо: = - + +С
Відповідь. - + +С
