Рассмотрим участок электрической цепи (рис. 16)

Рис. 16.
Участок ветви, содержащий один или несколько источников энергии, является активным.
Положительные направления тока и напряжения указаны стрелкой.
Определим потенциалы точек c, d, e, b, предположив, что известен потенциал точки a-ja.
Для правильного выбора знаков следует помнить, что:
1) ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е. потенциал падает по направлению тока.
2) э.д.с., направленная от точки «с» к точке «d», повышает потенциал последней на величину E.
3) напряжение U=Uac положительно, когда потенциал точки а выше, чем потенциал точки с.
При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она ставится в направлении от точки высшего потенциала к точке низшего потенциала.
На рис. 16 ток протекает от точки «а» к точке «с», значит потенциал jс будет меньше ja на величину падения напряжения на сопротивлении R1, которое по закону Ома равно IR1:
jс = ja - IR1
На участке cd э.д.с. E1 действует в сторону повышения потенциала, следовательно:
jd = jс + E1 = ja - IR1+ E1
Потенциал точки «e» меньше потенциала точки «d» на величину падения напряжения на сопротивлении R2:
je = jd – IR2 = ja - IR1+ E1– IR2
На участке e в э.д.с. E2 действует таким образом, что потенциал точки «b» меньше потенциала точки «e» на величину E2:
jb = je – E2 = ja - IR1+ E1– IR2 – E2 = ja – I(R1+R2) + E1-E2 (15)
Чтобы наглядно оценить распределение потенциала вдоль участка цепи, полезно построить потенциальную диаграмму, которая представляет график изменения потенциала вдоль участка цепи или замкнутого контура.
По оси абсцисс графика откладываются потенциалы точек, а по оси ординат – сопротивления отдельных участков цепи. Для участка цепи рис. 16 распределение потенциала построено на рис. 17.

Рис. 16. Потенциальная диаграмма участка цепи.
Потенциальная диаграмма рис. 16 построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал ja принят равным нулю.
Точка цепи, потенциал которой условно принимается равным нулю, называется базисной.
Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса.
Обобщенный закон Ома.
Закон Ома выражаемый формулой  , определяет зависимость между током и напряжением на пассивном участке электрической цепи.
, определяет зависимость между током и напряжением на пассивном участке электрической цепи.
Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).
Из формулы 15 следует:
ja -jb=I(R1+R2)- E1+E2 (16)
На положительное напряжение на участке a – b Uab=ja -jb
Следовательно, Uab= I(R1+R2)- E1+E2 (17)
 (18)
(18)
Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.
Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-».
Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.
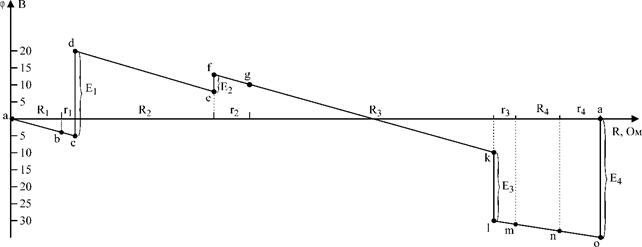
Пример № 1 построения потенциальной диаграммы:
Построить потенциальную диаграмму для одноконтурной схемы:

E1=25В; E2=5В; E3=20В; E4=35В,
R1=8 Ом; R2=24 Ом; R3=40 Ом; R4=4 Ом,
r1=2 Ом; r2=6 Ом; r3=2 Ом; r4=4 Ом.
Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r1- r4) за их пределы; обозначим точки контура.

Рис.2
2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:

3. За базисную точку примем точку a. Найдем потенциалы остальных точек:
jb = ja – IR1 = - 4В je = jd – IR2 = 8В
jc = jb – Ir1 = - 5В jf = je + E2 = 13В
jd = jc + E1 = 20В jq = jf – Ir2 = 10В
jk = jq – IR3 = - 10В jn = jm – IR4 = - 33В
je = jk – E3 = - 30В jo = jn – Ir4 = - 35В
jm = je – Ir3 = - 31В ja = jo + E4 = 0
4. В системе координат строим потенциальную диаграмму:
Законы Кирхгофа.
Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.
Законы Кирхгофа наряду с законом Ома являются основными в теории электрических цепей.
Первый закон Кирхгофа:
Алгебраическая сумма токов в узле равна нулю:
SIi = 0 (19)
Где i - число ветвей, сходящихся в данном узле.
Т.е., суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.

Рис.17. Иллюстрация к первому закону Кирхгофа.
Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:
Nуp = Nу – 1,
Где Nу – число узлов в рассматриваемой цепи.
Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.
Например, для узла, представленного на рис.17: припишем токам, подтекающим к узлу знаки «+», а к токам, оттекающим от узла – знаки «-».
Тогда уравнение по первому закону Кирхгофа запишется так:
I1 – I2 + I3 – I4 = 0.
Уравнения, составленные по первому закону Кирхгофа, называются узловыми.
Этот закон выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
Второй закон Кирхгофа:
Алгебраическая сумма э.д.с. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:
S Ui = S Ei
S IiRi = S Ei (20)
Где i – номер элемента(сопротивления или источника напряжения) в рассматриваемом контуре.
**Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:
Nуp = Nb – Nу + 1 – Nэ.д.с.
Где Nb – число ветвей электрической цепи;
Nу - число узлов;
Nэ.д.с. - число идеальных источников э.д.с.

Рис.18. Иллюстрация ко второму закону Кирхгофа.
Для того, чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнять следующие правила:
1. произвольно выбрать направление обхода контура, например, по часовой стрелке (рис.18).
2. э.д.с. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если э.д.с. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «-».
Например, для контура рис.18, второй закон Кирхгофа запишется следующим образом:
U1 – U2 + U3 = E1 – E3 – E4 (21)
Уравнение (20) можно переписать в виде:
S (Ui – Ei) = 0 (22)
Где (U – E) – напряжение на ветви.
Следовательно, второй закон Кирхгофа можно сформулировать следующим образом:
Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.
Потенциальная диаграмма, рассмотренная ранее, служит графической интерпретацией второго закона Кирхгофа.
Задача №1.
В схеме рис.1 заданы токи I1 и I3, сопротивления и э.д.с. Определить токи I4, I5, I6; напряжение между точками a и b, если I1 = 10мA, I3 = -20 мA, R4 = 5kОм, E5 = 20B, R5 = 3kОм, E6 = 40B, R6 = 2kОм.
.
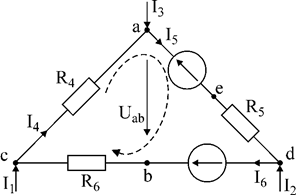
Рис.1
Решение:
1. Для заданного контура составим два уравнения по первому закону Кирхгофа и одно – по второму. Направление обхода контура указано стрелкой.

В результате решения получаем: I6 = 0; I4 = 10мA; I5 = -10мA
2. зададим направление напряжения между точками a и b от точки «a» к точке «b» - Uab. Это напряжение найдем из уравнения по второму закону Кирхгофа:
I4R4 + Uab + I6R6 = 0
Uab = - 50B.
Задача №2.
Для схемы рис.2 составить уравнения по законам Кирхгофа и определить неизвестные точки.
Дано: I1 = 20мA; I2 = 10мA
R1 = 5kОм, R3 = 4kОм, R4 = 6kОм, R5 = 2kОм, R6 = 4kОм.

Рис.2
Решение:
Число узловых уравнений – 3, число контурных уравнений – 1.
Запомнить! При составлении уравнения по второму закону Кирхгофа выбираем контур, в который не входят источники тока. Направление контура указано на рисунке.
В данной цепи известны токи ветвей I1 и I2. Неизвестные токи I3, I4, I5, I6.

Решая систему, получаем: I3 = 13,75 мA; I4 = -3,75мA; I5 = 6,25мA; I6 = 16,25мA.






