Рассмотрим две индуктивно связанные катушки,соединенные последовательно (рис 5.3). Каждая из катушек обладает индуктивностью L1 и L2 и активным сопротивлением проводника из которого катушка изготовлена r1 и r2. Индуктивная связь на электрической схеме указана двусторонней стрелкой и взаимной индуктивностью М.
Рис 5.3.
Одноименные зажимы катушек обозначены жирными точками и расположены так, что протекающий под воздействием напряжения u ток i вызывает в катушках одинаковое направление потоков. Поэтому включение называется согласным.
Запишем уравнение представленной на рис 5.3 цепи в мгновенных значениях токов и напряжений
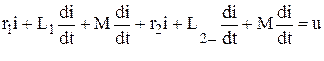
Для комплексов действующих значений токов и напряжений последнее уравнение примет вид:
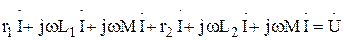
Перепишем это уравнение следующим образом:
Выражение в квадратных скобках называется сопротивлением двух последовательно соединенных индуктивно связанных катушек при согласном включении
Выражение в круглых скобках называется полной индуктивностью двух последовательно соединенных индуктивно связанных катушек при согласном включении
Очевидно Zсогл >Z, где Z-полное сопротивление двух последовательно соединенных катушек без индуктивной связи:
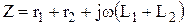
Увеличение сопротивления Zсогл происходит за счет увеличения полной индуктивности Lсогл.
Построим векторную диаграмму двух последовательно соединенных индуктивно связанных катушек при согласном включении. Для этого задаемся вектором тока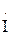 
. Напряжение на активном сопротивлении первой катушки 
совпадает по фазе с током. Напряжение на индуктивности первой катушки 
опережает ток на 900. Откладываем этот вектор с конца вектора под прямым углом k току 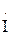. Напряжение на первой катушке, вызванное индуктивной связью 
также опережает ток на 900. Откладываем этот вектор с конца вектора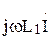 
. Напряжение на активном сопротивлении второй катушки 
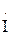совпадает с током . Напряжение на второй индуктивности 
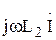и напряжение на второй катушке обусловленное взаимной индуктивностью опережает ток на 900.
Откладываем вектора напряжения в таком же порядке: следующий вектор откладывается с конца предыдущего.
В результате получим векторную диаграмму изображенную на рис 5.4.
Рис.5.4
Соединяя начало вектора и конец последнего вектора , получим напряжение 
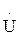. Сумма первых трех векторов напряжения дает напряжение на первой катушке 
. Напряжение на второй катушке 
, получается как сумма последних трех векторов напряжения.
