Для схемы, представленной на рис.6.10 уравнение электрического равновесия будет иметь вид:
;
;
;
Решение данной системы уравнений:
(6.13)
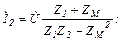
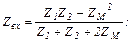
Соответствующие векторные диаграммы строятся аналогично случая последовательного соединения данных катушек.
6.2.5. Расчет разветвлённых цепей при наличии взаимной индуктивности
Расчёт разветвлённых цепей при наличии взаимной индуктивности представляется более сложным этапом. Он осуществляется с помощью законов Кирхгофа либо методов контурных токов. Отметим, что метод узловых потенциалов в данном случае не применим, поскольку токи в ветвях определяются не только разностью потенциалов соседних узлов, но и токами других ветвей, с которыми они связаны индуктивно. Пусть имеются три индуктивно связанные катушки, намотанные на общий сердечник, выполненный из немагнитного материала и подключённые к двум источникам ЭДС. Получим электрическую схему вида (рис.6.10).
Выберем в качестве расчётного метод контурных токов и составим систему уравнений относительно заданных на схеме контурных токов.
Решив систему, получим: 
; 
; 
.
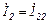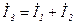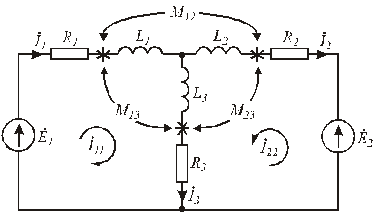
Рис.6.10. Электрическая схема с индуктивно
связанными катушками
6.2.6. "Развязывание" магнитосвязанных цепей
Отличительной особенностью расчёта цепей со взаимной индуктивностью является то, что приходится одновременно учитывать электрические и магнитные связи. Расчёт цепей упростится, если теми или иными методами исключить магнитную связь и свести данную цепь к чисто электрической. Это возможно, если прибегнуть к развязыванию магнитных связей, при этом в составе цепи появятся новые дополнительные элементы.
В схеме рис.6.11 катушки L1 и L2 индуктивно связаны. Рассмотрим два варианта их соединения. В узле С они могут соединяться как одноименными, так и разноименными зажимами.
1) Пусть в узле С катушки соединены разноимёнными зажимами. Составим уравнения по законам Кирхгофа с учётом индуктивной связи.
Рис.6.11. Исходная цепь
Преобразуем систему уравнений к следующему виду:
или
Рис.6.12. Схема после "развязывания" магнитных связей при соединении катушек в узле разноименными зажимами
2) Если в узле С катушки соединены одноимёнными зажимами, аналогичные рассуждения позволили бы получить следующую схему:
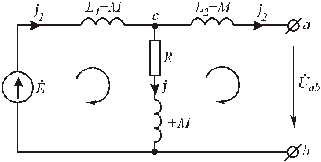
Рис.6.13. Схема после «развязывания» магнитных связей при
соединении катушек в узле одноименными зажимами
Для обоих случаев определим выражения 
при условии 
, получим: 
, 
.
Для разноимённого соединения:
. (6.14)
Для одноимённого соединения:
. (6.15)
Оставаясь неизменным по модулю в обоих случаях, в первом случае напряжение отстаёт на определённый угол, а во втором варианте - опережает ток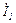 
. При этом ток 
не зависит от способа соединения катушек:
;
Появление параметра М в процессе процедуры развязывания говорит о том, что в состав цепи искусственно вводится некоторая дополнительная индуктивность М. Для рис.6.12 введенный элемент с сопротивлением (- jωM) имеет емкостной характер, для рис.6.13 – индуктивный (jωM).
