Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.
Пусть дана некоторая электрическая цепь, которую представим активным двухполюсником (рис.3.10). Необходимо рассчитать ток в ветви ab:
1) введем в ветвь ab два источника ЭДС. 
и 
одинаковые по величине и противоположно направленные:
;
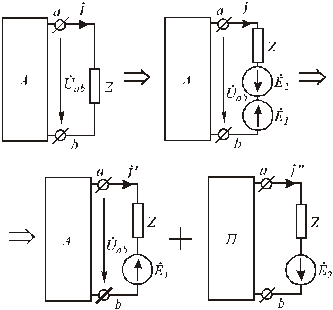
Рис.3.10. Преобразование исходного двухполюсника
в сумму двух цепей
2) используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС . Вторая цепь представляет собой пассивный двухполюсник и источник ЭДС 
.
На основании принципа наложения ток ветви ab:
;
; 
.
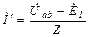Поскольку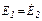 
– любые по величине, то подберем их значения такими, чтобы ток 
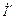был равен нулю. Для этого выберем 
.
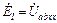Напряжение на зажимах источника в режиме холостого хода численно равна его ЭДС. Тогда активный двухполюсник с источником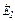 
может быть представлен в виде:
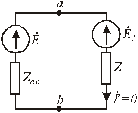
Рис.3.11. Схема замещения активного двухполюсника
В этой схеме эквивалентная ЭДС активного двухполюсника:
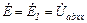
и, следовательно, ток
.
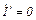Таким образом, ток в ветви ab:
. 89(3.15)
Пусть дана цепь (рис.2.12), рассчитаем ток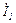 
методом эквивалентного генератора.
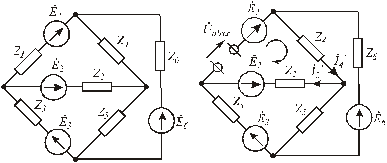
Рис.3.12. Исходная цепь
Последовательность расчета:
1. Разомкнем ветвь с сопротивлением Z1 или примем Z1 = ¥.
2. Зададим положительное направление 
и для произвольно выбранных положительных направлений токов, например, первого контура, запишем уравнение по второму закону Кирхгофа:
.
3. Ток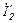и 
и 
в преобразованной схеме (рис.3.13) рассчитываем любым известным методом, например, методом контурных токов:
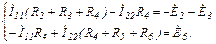
Тогда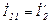 
; 
.
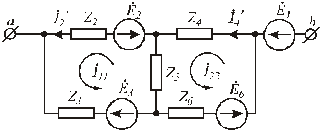
Рис.3.13. Преобразованная цепь
4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя для реальных источников их внутренние сопротивления.
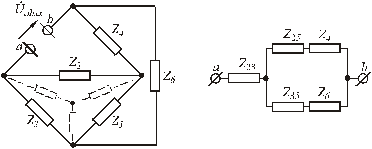
Рис.3.14. Схема пассивного двухполюсника
В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов a-b, так как нет последовательно-параллельного соединения приемников, поэтому необходимо выполнить преобразование какого-либо участка цепи из «треугольника» в «звезду» или выполнить обратное преобразование.
Заменим, например, треугольник сопротивлений Z2 – Z3 – Z5 в звезду Z23 – Z25 – Z35. При этом получится схема с последовательно-параллельным соединением приемников (рис.3.14.в).
Сопротивления этой схемы:
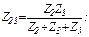
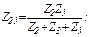
и эквивалентное сопротивление:
.
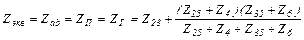Окончательно:
.
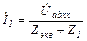ТРЕХФАЗНЫЕ ЦЕПИ
В предыдущей главе рассматривалась работа электрических цепей, питающихся от однофазных синусоидальных источников тока или напряжения. Наряду с однофазными источниками существуют источники энергии, количество фаз у которых составляет два, три, четыре и т.д., и которые характеризуются тем, что ЭДС этих фаз имеют одинаковую частоту, но сдвинуты друг относительно друга на некоторую одинаковую фазу. Такие генераторы называются многофазными и электрические цепи с такими источниками называются многофазными.
Трехфазный генератор
Среди всего многообразия многофазных источников трехфазный получил наибольшее практическое применение. В связи с этим основные исследования многофазных цепей будем проводить на примере трехфазных цепей. И в связи с этим рассмотрим вопрос реализации такого трехфазного источника, которым является трехфазный генератор.
Рис.4.1. Трехфазный генератор
В целях упрощения понимания принципа работы генератора обмотки представлены одним витком. В качестве ротора генератора выбран постоянный магнит. Каждая из обмоток имеет начало – клеммы А, В, С и конец – Х, Y, Z. Обмотки в пространстве сдвинуты на 120° друг относительно друга. Из чего следует, что максимумы ЭДС в них достигаются в разные моменты времени, отстоящие друг от друга на одну треть периода T = 2p / w, где w - угловая часта вращения ротора.
Последовательность, в которой ЭДС достигают максимума в соответствующих фазах, носит название порядка чередования фаз. Прямым порядком чередования фаз называют последовательность, при которой фаза B отстает от фазы А на 1/3Т, и фаза С отстает от фазы В на 1/3Т – т.е. А, В, С. На рис.4.2 изображен график мгновенных значений ЭДС для прямого порядка чередования фаз. Изменение направления вращения ротора на противоположное меняет эту последовательность чередования фаз и она станет уже А, С, В.
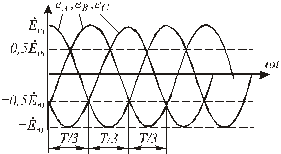
Рис.4.2. Графики мгновенных ЭДС фаз А, B, С
eА=Emsin(wt + p/2);
eВ=Emsin(wt + p/2 - 2p/3); 90(4.1)
eС=Emsin(wt + p/2 - 2p/3 - 2p/3).
Поскольку ЭДС каждой фазы генератора синусоидальна, то им в соответствие можно на комплексной плоскости построить векторы фазных ЭДС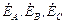 
(рис.4.3).
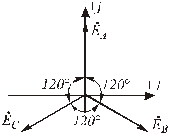
Рис.4.3. Векторная диаграмма фазных ЭДС
Важным обстоятельством является то, что система векторов фазных ЭДС генератора на комплексной плоскости образует симметричную трехлучевую звезду, и сумма этих векторов в любой момент времени равна нулю.
При подключении к каждой из фаз генератора нагрузки по ней будет протекать ток. Таким образом, образуется трехфазная система.
