Используя метод контурных токов, можно получить обобщенное уравнение по расчету любого i -го контурного тока. Сомножитель перед 
имеет размерность Ом – 1, то есть уравнение будет иметь следующий вид:
.85
В общем случае это уравнение применимо для любого i -го контурного тока, однако, оно справедливо и для любого реального тока в ветви, так как всегда можно систему независимых контуров выбрать так, чтобы ток ветви численно равнялся контурному току. Если в уравнении (2.8) учесть, что контурная ЭДС есть сумма всех ЭДС контура, то, перегруппировав слагаемые таким образом, чтобы каждая ЭДС умножалась на соответствующую сумму слагаемых вида 
, получим уравнение для тока ветви.
(3.11)
В правой части уравнения (3.11) имеем сумму слагаемых – токов, созданных каждой из ЭДС ветви в отдельности.
Принцип наложения: ток любой i -ой ветви равен алгебраической сумме токов, созданных каждой из ЭДС цепи в отдельности.
Рис.3.3. Иллюстрация принципа наложения
На сформулированном принципе базируется метод наложения, суть которого состоит в следующем: в исходной электрической цепи поочередно закорачиваются все источники ЭДС, кроме одного и производится расчет частичных токов в ветвях любым из известных методов.
Для определения реальных токов в исходной цепи производится алгебраическое суммирование этих частичных токов:
;
;
.
Входные и взаимные проводимости
Пусть дана некоторая электрическая цепь, содержащая единственный источник ЭДС в k -ой ветви. Кроме того, выделим еще одну ветвь – m -ю, а всю оставшуюся часть электрической цепи представим в виде некоторого пассивного четырехполюсника (рис.3.4).
Рис.3.4. Схема пассивного четырехполюсника
Определим k -й и m -й токи. Используя уравнение (3.11), запишем выражение для k -го и m -го токов:
;
.
Если Ek = 1В, то 
; 
;
k- й и m- й токи численно равны своим проводимостям, при условии, что Ek = 1В. Ykk – входная проводимость k – ой ветви. Ykn – взаимная проводимость k – ой и m - ой ветви. Рассмотрим пример определения входных и взаимных проводимостей (рис.3.5).
Рис.3.5. Схема замещения пассивного четырехполюсника
Представим пассивный четырехполюсник в виде схемы рис.3.5 и составим для нее уравнения по методу контурных токов.
;
;
;
;
;
.
Свойство взаимности
Рассмотрим еще одно важное свойство, имеющее место в сложных цепях, присущее линейным электрическим цепям, базирующееся на понятиях входных и взаимных проводимостей.
Рис.3.6. Схемы, иллюстрирующие принцип взаимности
;
.
Докажем, что взаимные проводимости Ykk и Ykn равны. Пусть для некоторой многоконтурной схемы составлена система уравнений по методу контурных токов, и главный определитель системы имеет вид:
Этот определитель всегда симметричен относительно первой главной диагонали, проходящей через элементы Z11 – Znn, т.к. любой элемент Zkm=Zmk (сопротивления, расположенные на границе k- ого и m- ого контуров). У такого определителя строка m не отличается от столбца k и поэтому алгебраические дополнения, полученные вычеркиванием k- ой строки и m- ого столбца и наоборот, равны, следовательно:
. 86(3.12)
Пусть 
и 
Þ 
;
Свойство взаимности: если ЭДС k- ой ветви вызывает в m- ой ветви ток Im, то, будучи перенесенным в m- ю ветвь, этот же источник вызовет ток той же амплитуды и фазы в k- ой ветви.
Цепи, обладающие такими свойствами, носят название обратимых цепей. Все линейные цепи обратимы.
3.8. Преобразование треугольника сопротивлений в эквивалентную звезду и обратное
преобразование
При расчете разветвленных цепей и, особенно, при определении их входных сопротивлений может возникнуть вопрос о преобразовании треугольника сопротивлений в эквивалентную звезду или обратного преобразования. Такая процедура становится возможной при условии неизменности потенциалов на зажимах преобразуемого участка цепи.
Рассмотрим участок цепи, соединенный треугольником (рис.3.7).
Составим уравнения по первому и второму законам Кирхгофа для «треугольника».
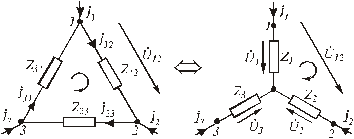
Рис.3.7. Взаимное преобразование «треугольника» в «звезду»
По первому закону Кирхгофа:
«1 узел»: 
;
«2 узел»: 
.
По второму закону Кирхгофа:
.
Решим эту систему уравнений, например, относительно тока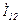 
:
Определим напряжение 
:
в схеме «треугольник»:
;
в схеме «звезда»:
Причем, должно выполняться такое равенство: 
. Приравнивая эти выражения, получим формулы перехода от соединения сопротивлений «треугольником» к сопротивлениям «звезды»:
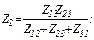
.87(3.13)
Покажем на примере применимость данного преобразования.
Рис.3.8. Преобразование «треугольника»
сопротивлений в «звезду»
Рис.3.9. Преобразование «звезды»
сопротивлений в «треугольник»
Обратное преобразование - из «звезды» в «треугольник» выполняется по формуле перехода:
88(3.14)
