Последовательное соединение

 

Рис.2.11. Последовательное соединение R, L, C

 

На основании второго закона Кирхгофа:

u = u_R + u_L + u_C;

u = iR +L + . 36(2.26)

Перейдем к комплексным изображениям:

i = I_msin(wt+y_i) Þ _. 37(2.27)

Используя полученный комплекс тока, определим комплексы падения напряжения на участках цепи:

Для сопротивления:

, (2.28)

где 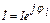. 38

Для индуктивности:

. 39(2.29)

Для емкости:

. 40(2.30)

Найденные комплексы U_R,U_C,U_{L ,} подставим в исходное уравнение:

, 41(2.31)

. 42(2.32)

- закон Ома в комплексной форме.

Выражение в знаменателе представляет собой комплексное сопротивление исходной цепи, которое имеет вещественную и мнимую составляющую.

, 43(2.33)

где ; .

Для комплексных амплитуд закон Ома запишется в следующем виде:

, 44(2.34)

где U_m= I_mz - амплитуда напряжения;

 

Рис.2.12. Изображение сопротивления
на комплексной плоскости

 

φ_U = j + j_i; Þ j = j_U – j_i; 45(2.35)

u(t) = U_msin(wt + j_U). 46(2.36)

Построим векторную диаграмму цепи.

 

Рис.2.13. Векторная диаграмма для последовательного
колебательного контура

 

i(t) = I_msin(wt + j_i); j_i > 0.

Построение векторной диаграммы начинают с вектора тока, т.к. он одинаков на всех участках цепи. Из построенной на комплексной плоскости векторной диаграммы можно выделить векторный треугольник напряжений, представленный на рис.2.14.

 

Рис.2.14. Векторный треугольник напряжений

Ниже приведен треугольник сопротивлений.

 

Рис.2.15. Скалярный треугольник сопротивлений

 

Угол сдвига фаз между током и напряжением можно определить из любого треугольника.

. 47(2.37)

Резонанс напряжений

Резонансом в цепях переменного тока, содержащих индуктивные и емкостные элементы, называется явление совпадения по фазе векторов тока и напряжения на входе цепи или на участке цепи, при этом cosj = 1, j = 0.

Резонанс напряжений наблюдается в последовательном колебательном контуре. На рис.2.16 построена векторная диаграмма для этого режима.

 

Рис.2.16. Векторная диаграмма для резонанса напряжений

 

При резонансе:

X_Cp = X_Lp или ,

, 48(2.38)

где w₀ –циклическая частота последовательного колебательного контура.

Резонанс достигается путем изменения одного из пара­метров w, L, C при двух других фиксированных.

Определим индуктивное и емкостное сопротивления цепи при резонансе:

49(2.39)

50(2.40)

Величина r, называется волновым сопротивление контура.

Введем еще один важный параметр, характеризующий резонанс – добротность контура:

. 51(2.41)

Добротность (коэффициент резонанса) – это отношение напряжения на индуктивности или напряжения на емкости к входному напряжению цепи.

Рассмотрим энергетические соотношения в цепи при резонансе напряжений. Определим суммарную энергию, потребляемую реактивными элементами из сети.

w = w_M+w_Э ;

;

;

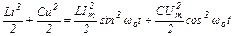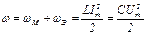. 52(2.42)

Суммарная энергия электрического и магнитного полей при резонансе остается величиной постоянной.

Рассмотрим частотные характеристики цепи при резонансе. В случае, когда на последовательную цепь воздействует источник сину­соидального напряжения с частотой w, меняю­щейся от 0 до ¥, параметры цепи, а именно ее реактивное и полное сопротивления меняются, что вызовет соответству­ющие изменения тока и падений напряжения на отдельных участках цепи.

Построим функции названных выше сопротив­лений в одних координатных осях (рис.2.17).

Исходя из построений (рис.2.17), можно заключить, что в доре­зонансной области частот – [ 0; w_o) преобладает емкостной харак­тер нагрузки, а после резонансной области (w_o; ¥) индуктив­ный, и в точке резонанса (w_о) реактивное сопротивление равно нулю, характер нагрузки активный. На рис.2.18 представлены зависимости падений напряжения, тока и фазы последовательного колебатель­ного контура от частоты.

 

Рис.2.17. Зависимости сопротивлений цепи от частоты w

 

Рис.2.18. Кривые изменений напряжений, тока и фазы
последовательного колебательного контура от частоты

 

Рис. 14.

На нулевой частоте (для источника постоянного ЭДС) индуктивность заме­няется короткозамкнутым проводником, а емкость обрывом; на бесконечной частоте свойства указанных элементов меняются местами, то есть индуктивность становится обрывом, а емкость - короткозамкнутым проводником.

Значения функции j(w) не существуют при w = 0 и w = ¥.

Оценим влияние параметров цепи на форму резонансной кривой тока. Решение этого вопроса начнем с уже известной нам функции , с которой сделаем следующие преобразования:

.

Используя полученное выражение для входного сопротивления z, определим ток:

53(2.43)

где I_o – максимальное значение тока в цепи при резонансе.

 

Рис.2.19. Резонансные кривые: Q₃ > Q₂ > Q₁

 

Для удобства построение будем вести в относительных единицах (график зависимости см. на рис.2.19):

;