Параллельное соединение элементов R, L, C

Рассмотрим параллельное соединение разнородных элементов
R, L, C.

Рис.2.20. Схема параллельного соединения элементов R, L, C

Пусть на вход цепи подано напряжение u = U_msin(wt+j_u), тогда по первому закону Кирхгофа:

Комплексное изображение входного напряжения:

.

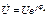Для определения комплекса общего тока найдем его составляющие:

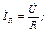
тогда комплекс общего тока:

. 54(2.44)

Построим векторную диаграмму для параллельного соединения (рис.2.21).

Пусть φ_u < 0, φ_u - φ_I = j > 0, j - опережающий, характер нагрузки активно-индуктивный.

Выражение в круглых скобках (2.44) имеет размерность 1/Ом или См (симменс) и носит название комплексной проводимости цепи:

, 55(2.45)

где y – модуль комплексной проводимости, а j – угол сдвига фаз между током и напряжением.

 

Рис.2.21. Векторная диаграмма для параллельного соединения разнородных элементов

 

Комплексная амплитуда общего тока:

. 56(2.46)

Её модуль:

.

Её фаза:

;

.

Мгновенное значение общего тока:

i = I_msin(wt + φ_u – j).

Проводимости

Под комплексной проводимостью любой цепи понимается величина обратная ее полному комплексному сопротивлению:

, 57(2.47)

где g – активная проводимость данной цепи;

b – результирующая реактивная проводимость.

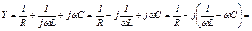
, 58(2.48)

где b_L и b_C – индуктивная и емкостная проводимости соответственно.

Понятие проводимости приобретает особый смысл в том случае, если ветвь содержит активные и реактивные элементы. На ветви, изображенной на рис.2.22, определим ее активную и реактивную проводимости:

 

Рис.2.22. Участок цепи с активно-индуктивным сопротивлением

 

. 59(2.49)

Из векторной диаграммы (рис.2.21) можно выделить треугольник токов:

 

Рис.2.23. Векторный треугольник токов

 

Разделив стороны векторного треугольника токов на вектор напряжения, получим скалярный треугольник проводимостей.

 

Рис.2.24. Скалярный треугольник проводимостей

Резонанс токов

Резонансный режим, возникающий при параллельном соединении R, L, C, называется резонансом токов. В отличие от рассмотренного ранее режима резонанса напряжений, данный режим не столь однозначен.

Рис.2.25. Цепь с параллельным соединением
разнородных приемников

 

В цепи (рис.2.25) режим резонанса токов возникает при условии равенства нулю результирующей реактивной проводимости этой цепи:

b = b₁+ b₂ = 0. 60(2.50)

Реактивные проводимости ветвей:

.

Подставим выражения b₁ и b₂ в (2.50):

и после преобразования получим резонансную частоту :

. 61(2.51)

Структура полученного уравнения показывает, что существует четыре варианта частоты :

1. Если R₁ = R₂ ¹ r, то = w₀

2. Если R₁ = R₂ = r, то = w₀ – с физической точки зрения это означает, что входное сопротивление данного контура равно ее волновому, которое не зависит от частоты, значит, резонанс будет иметь место при любой частоте. Для доказательства этого положения определим входное сопротивление цепи:

3. Если под корнем получилось отрицательное число, значит, резонансной частоты не существует для данных параметров R₁, R₂, r, L, C.

4. Если под корнем положительное число, то получаем - единственную резонансную частоту.