Цепи однофазного синусоидального тока

КУРС ЛЕКЦИЙ

ПО ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

 

Тюмень "Вектор Бук", 2001

 

 

УДК 621.3(075)

 

Шлык Ю.К., Кречина Г. С.. Курс лекций по теории электрических цепей. Тюмень, «Вектор Бук», 2001 г. 250 с.

В данном учебном пособии изложены основные методы расчета сложных электрических цепей. При этом рассмотрены линейные и не линейные цепи, работающие как в установившихся, так и в переходных режимах.

Рассмотрена теории четырехполюсников и электрических линий с распределенными параметрами.

Все основополагающие научные позиции, изложенные в пособии, подтверждены конкретными практическими расчетами.

Книга предназначена для студентов электроэнергетических специальностей соответствующих институтов и университетов РФ.

Рис.,список лит. наименований.

Авторы выражают глубокую благодарность кафедре «Электроэнергетики» ТюмГНГУ, и лично, ее зав. кафедрой – д. т. н., профессору Кицису С. И. за научно-методическую редакцию данной работы.

Кроме того, авторы признательны студентам, принявшим активное участие в подготовке и оформлении данной рукописи к изданию: Красноперову А. Г., Морозову С. А., Шлыку К. Ю., Шульгину Д. В.

 

 

 

 

Предисловие

Курс теории электрических цепей является составной частью курса теоретических основ электротехники (ТОЭ). Это фундаментальная наука, базирующаяся на исследованиях в области электрических и магнитных явлений.

В том виде, как мы ее знаем, она возникла сравнительно недавно – в начале ХХ века, однако путь, который она прошла, был достаточно долгим и трудным. Потребовалось достаточно много творческих усилий как наших, так и зарубежных ученых, чтобы внешне разрозненные явления природы были систематизированы и выстроены в строгую теорию.

Без электрической энергии сегодня не возможно представить нашу жизнь. Она применяется по всюду и потребность в ней неуклонно возрастает. Столь широкое распространение этого вида энергии не случайно, ибо ее можно передавать на огромные расстояния от источника до потребителя. Она способна легко трансформироваться в другие виды, такие как: механическую, химическую, световую и др. При этом возможен и обратный ее переход, что подтверждает универсальность данного вида энергии.

Развитие электроэнергетики, как науки, потребовало больших усилий в области изучения электромагнитных явлений и их практического применения. Работы в этом направлении начались давно. Первый трактат по электричеству вышедший в 1753 г., принадлежит нашему великому соотечественнику М. В. Ломоносову – «Слово о явлениях воздушных, от электрической силой происходящих», посвященный теории атмосферного электричества.

Потребовалось более чем полвека, прежде чем А. Вольта изобрел свой гальванический столб. Все это позволило впервые получить реальный электрический ток.

Первые годы XIX века явились началом развития теории и практики цепей постоянного тока. В этой связи приведем хронологическую последовательность открытий, положивших начало систематическому изучению электрических и магнитных явлений.

Рассматривая хронологию развития данной науки, выделим основные ее даты.

1802 г. – В. В. Петров обнаружил и исследовал явление электрической дуги между двумя угольными электродами. Он указал на возможность ее использования для освещения, плавки и сварки металлов.

1819 г. – Эрстед обнаружил механическое воздействие электрического тока на магнитную стрелку.

1820 г. – Ампер открыл магнитные свойства соленоида с током.

1831 г. – Фарадей открыл и впервые описал явление электромагнитной индукции.

1833 г. – Э. Х. Ленц (русский академик) открыл фундаментальный принцип электродинамики – принцип электромагнитной инерции; он же в 1844 г., не зависимо от Джоуля, открыл закон о тепловом действии электрического тока.

1845 г. – Кирхгофф сформулировал основные законы для разветвленных электрических цепей, имеющие фундаментальное значение.

1876 г. – П. Н. Яблочков (русский инженер) изобрел электрическую свечу, которая положила начало электрическому освещению; он же был и автором реализации использования переменного электрического тока, а так же создал первый в мире трансформатор.

Период времени с 1800 по 1880 гг. можно считать периодом становления теории и практики цепей постоянного тока.

С открытием П. Н. Яблочковым переменных токов начался новый этап развития электротехники. Переменный ток получил исключительно широкое практическое применение благодаря изобретениям русского инженера М. О. Доливо-Добровольского.

1889 г. – М. О. Доливо-Добровольский построил первый 3-х фазный электрический двигатель и разработал все основные звенья 3-х фазной электрической цепи, он же в 1891 г. осуществил передачу электроэнергии 3-х фазным током на расстояние 175 км.

Применение переменных токов потребовало решения целого ряда теоретических и практических задач, существенно отличающихся от задач по расчету цепей постоянного тока. Важнейшим этапом здесь можно считать введение американским инженером Штейнметцем комплексного метода расчета цепей переменного тока.

Создание первых электрических машин (электрических двигателей и трансформаторов), а так же линии электропередач потребовало исследований по расчету электрических и магнитных полей, а так же их совокупности – единого электромагнитного поля.

1888 г. – Герц экспериментально доказал существование поля излучения, теоретически предсказанного Максвеллом в 1873 г. Однако сам Герц и многие другие физики не верили в возможность использования электромагнитных волн для беспроводной связи.

1895 г. – А. С. Попов (русский инженер) блестяще решил практическую задачу по передаче информации с помощью электромагнитных волн. Изобретение радиосвязи открыло новую эру в культурной жизни человечества (первые слова эфира были «Генрих Герц»).

1. Основные определения, понятия и
законы в теории электрических цепей

Электрическая цепь – это совокупность устройств, пред­назна­ченных для передачи, распределения и взаимного преоб­разования электрической энергии, если процессы, протека­ющие в этих устрой­ствах, могут быть определены с помо­щью понятий ЭДС, тока и напряжения.

Электрическая схема – это изображение электричес­кой цепи с помощью условных обозначений. Несмотря на всё многообразие цепей, каждая из них содержит эле­менты двух основных типов – это источники токов и потреби­тели.

 

а) b) с)

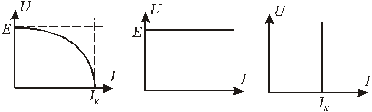
Рис.1.1.Вольтамперные характеристики источников ЭДС (a,b), источников тока (с)

 

Источники энергии (см. рис.1.1) могут быть двух типов: источники ЭДС (напряжения) и источники тока. Любой реальный источник напряжения харак­теризуется двумя основными параметрами: величи­ной ЭДС Е и вели­чиной его внутреннего сопротивления R_вн (рис.1.2). Напряжение на зажимах ис­точника в режиме холостого хода численно равно ЭДС.

 

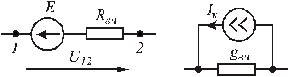
a) b)

Рис.1.2. Реальный источник ЭДС (a) и источник тока (b)

 

Реальный источник тока характеризуется величиной тока I_к и внутренней проводимостью g_вн. Наряду с реальными рассмотрим два их идеализиро­ванных варианта.

Для источника ЭДС (рис.1.2.a) положительное направление ЭДС указывается стрелкой, т.е. U₁₂ = φ₁ – φ₂, напряжение убывает от точки с большим потенциалом к точке с меньшим по­тенциалом.

В случае, когда внутреннее сопротивление источника равно нулю (R_вн = 0), реализуется классический вариант идеализированного источника ЭДС. Напряжение на зажимах такого источника не зави­сит от силы тока, который через него протекает (рис.1.1.b). В случаях, когда R_вн << R_нагр, источник ЭДС можно считать идеальным.

Другим вариантом идеального источника энергии является источник тока, для которого g_вн=0 (рис.1.1.с). Ввиду того, что источник тока имеет бесконечное внутреннее сопротив­ление, ток, протекающий по нему, остается постоянным, а напряжение на зажи­мах может быть любым.

Поскольку физические свойства идеализированных источников коренным обра­зом различны, то прямая их замена друг на друга невозможна. Тем не менее, процедура преобра­зования одного реального источника в другой возможна и широко применяется на практике (рис.1.2).

Е = 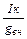, 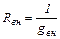. 1(1.1)

Потребители классифицируются по трем основным типам: сопротивление R, индуктивность L и емкость C (рис.1.3).

 

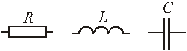
Рис.1.3. Потребители в электрических цепях

 

Сопротивление – идеализированный пассивный элемент цепи, приближенно заменяющий резистор, в котором происходит необратимый процесс преобразования электрической энергии в неэлектрические виды энергии.

R = U/i, Ом.

Вольт-амперные характеристики (ВАХ) линейного (1) и нелинейного (2) сопротивлений изображены на рис.1.4.

 

Рис.1.4. Вольт-амперные характеристики линейного (1) и нелинейного (2) сопротивлений

 

Индуктивность – идеализированный пассивный элемент цепи, приближенно заменяющий катушку индуктивности, в которой происходит процесс накопления энергии магнитного поля.

L = y/i, Гн; y = WФ, Вб. 2 (1.2)

Вебер-амперные характеристики линейной (1) и нелинейной (2) индуктивности представлены на рис.1.5.

 

Рис.1.5. Вебер-амперные характеристики линейной (1)
и нелинейной (2) индуктивности

 

Ёмкость – идеализированный пассивный элемент цепи, приближенно заменяющий конденсатор, в котором происходит процесс накопления энергии электрического поля.

C = q/u, Ф.3 (1.3)

Кулон-вольтные характеристики линейной (1) и нелинейной (2) емкости представлены на рис.1.6.

Кроме того, любая цепь характеризуется следующими основными топологическими понятиями.

Ветвь – это участок цепи, состав­ленный из после­довательно соединен­ных элементов цепи и расположен­ный между двумя узлами.

Узел – это точка цепи, где сходятся три или более ветвей.

Контур – это замкнутый путь, про­ходящий по не­скольким ветвям (рис.1.7).

 

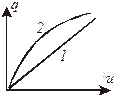
Рис.1.6. Кулон-вольтные характеристики линейной (1)
и нелинейной (2) емкости

 

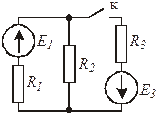
Рис.1.7. Электрический контур

 

Контур называется независимым, если в его составе при­сут­ствует хотя бы одна новая ветвь, ранее не входившая в другие контуры. В схеме на рис.1.7 при замкнутом ключе имеем три контура, но лишь два из них неза­висимы.

Закон Ома для участка цепи, не содержащего ЭДС:

I = U/R. (1.4)

Рассмотрим участок цепи с ЭДС (рис.2.1).

 

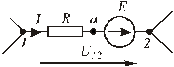
Рис.1.8. Линейный участок цепи, содержащий ЭДС

 

Из состава сложной электрической цепи выделим ветвь, содержащую источник энергии и потребитель. Для определенности примем, что направления тока и источника ЭДС совпадают. При условно выбранных положительных направлениях тока и ЭДС в ветви имеем:

j₁ > j_a Þ j₁ – j_a = IR, 4(1.5)

j₂ > j_a Þ j₂ – j_a = E. 5(1.6)

Вычтем из уравнения (1.5) уравнение (1.6) и тогда получим:

j₁ – j₂ = IR – E = U₁₂;

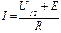. 6(1.7)

Полученное выражение представляет собой закон Ома для участка цепи с ЭДС. В случае несовпадения направления тока в ветви с направлениями напряжения и ЭДС перед ними появляется знак «минус».

 

Законы Кирхгофа

Первый закон Кирхгофа - алгебраическая сумма токов в узле равна нулю:

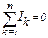. 7(1.8)

где k – номер ветви, n – общее их количество.

Второй закон Кирхгофа - алгебраическая сумма падений напряжений вдоль замкну­того контура равна алгебраической сумме ЭДС, действующих в этом контуре:

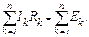8(1.9)

Второй закон Кирхгофа работает как для замкнутого, так и для разомк­нутого контура.

 

Уравнение баланса мощности:

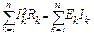9 (1.10)

Уравнение баланса мощности является модификацией закона сохранения энергии для электрических цепей. Это базовое уравнение для проверки правильности выполненных расчетов тех или иных цепей.

В левой части этого уравнения стоит арифметическая сумма мощностей, которые выделяются на сопро­тивлениях от токов, которые по ним протекают. В правой части – мощность, отданная источниками в сеть.

При этом возможна такая ситуация, когда одно из сла­гаемых суммы справа мо­жет оказаться отрицательным. Это будет означать, что в данной ситуации источник становится пот­ребителем. Она возникает в случае, когда ток, проте­кающий по источнику, направлен встречно направлению ЭДС.

ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА

Рассмотренные выше источники энергии могут быть как постоянными, так и переменными, причем закон их изменения во времени может носить как периодический, так и непериодический характер. Наибольшее практическое распространение получили источники, а, следовательно, и цепи, электромагнитные процессы, в которых подчиняются периодическому закону.

Частным случаем таких цепей являются цепи однофазного синусоидального тока.

Мгновенное значение любой синусоидальной функции: напряжения, тока, ЭДС и т.д. может быть представлено выражением вида:

u(t) = U_m sin(wt+y), 10(2.1)

где U_m – амплитуда – наибольшее значение функции за период Т (рис.2.1), аргумент синуса – (wt+y) – фаза колебания; w – круговая (циклическая) частота колебания; y – начальная фаза, которая показывает смещение синусоиды относительно начала координат вправо или влево,

T = 1/¦ Þ ¦ = 1/T, [Гц]; 11(2.2)

w = 2p¦ = 2p/Т, [рад/с]. 12(2.3)

 

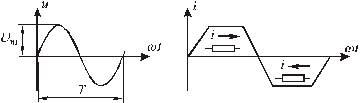
Рис.2.1. Примеры изображения периодических функций