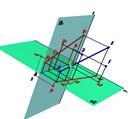
Построим пространственную модель, на которой изобразим две взаимно перпендикулярные плоскости П1 и П2. Линия пересечения плоскости П1 и плоскости П2 называется осью проекций и обозначается П2 / П1. Ось проекций совпадает с осью ОХ.

Выберем в пространстве точку А и опустим из неё на плоскости П1 и П2 перпендикуляры. Тогда мы получим две проекции точки А: А1 - первую или горизонтальную проекцию точки А и А2 - вторую или фронтальную проекцию точки А. Прямые А А1 и А А2 называются проецирующими прямыми или проецирующими лучами.
Перейдем от модели к чертежу. Для этого мысленно удалим точку А и повернём плоскость П1 вместе с отрезком А1 А0 вокруг оси проекций П2 / П1 до совмещения с плоскостью П2.
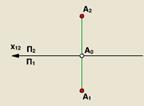
Полученный чертеж называется эпюром Монжа, ортогональным чертежом или комплексным чертежом.
Комплексный чертёж линии
Комплексный чертёж линии представляет собой совокупность проекций точек этой линии на две или три плоскости проекций. На комплексном чертеже необходимо установить связь между проекциями точек. В этом случае линия будет определена однозначно.
Например, возьмём прямую m общего положения, заданную двумя точками А и В. Построим ортогональные проекции отрезка АВ на плоскости П1, П2, П3. Соединив ортогональные проекции точек А и В на каждой плоскости, мы получим ортогональную проекцию отрезка АВ на все три проецирующие плоскости.

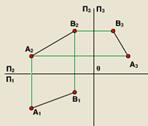
Теперь перейдём к ортогональному чертежу. По аналогии с тем как мы строили ортогональный чертёж точки, построим ортогональный чертёж отрезка АВ общего положения на все три плоскости проекций. Для этого сначала построим проекции точки А: А1, А2 и А3, затем проекции точки В: В1, В2 и В3. Соединим одноимённые проекции точек А и В. Мы получили комплексный чертёж отрезка прямой АВ общего положения на все три плоскости проекций.
Комплексные чертежи плоскостей
Рассмотрим пример комплексного чертежа плоскости общего положения, заданной тремя точками, не лежащими на одной прямой: А, В, С, т. е. треугольник АВС. Спроецируем точки А, В, С на все три плоскости проекций, и получим ортогональные проекции плоскости, заданной треугольником АВС. Каждая проекция плоскости АВС, есть треугольник.

Как на комплексном чертеже можно задавать прямые и плоскости?
Задание прямой
Двумя точками.
2. Двумя плоскостями (a; b).
3. Двумя проекциями.
4. Точкой и углами наклона к плоскостям проекций.
Задание плоскости на чертеже
а) проекциями трех точек, не принадлежащих одной прямой линии;
б) проекциями прямой и не принадлежащей ей точки;
в) проекциями двух пересекающихся прямых;
г) проекциями двух различных параллельных прямых;
д) проекциями плоской фигуры.
Как на эпюре располагаются проекции точек, прямых, плоскостей при следующих их взаимных расположениях:
Если точка С лежит на прямой:
Ответ:
Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой).
Из четырех предложенных на рисунке точек, только одна точка С лежит на прямой АВ.