16.1. Показати, що хімічний потенціал фотонного газу дорівнює нулю.
16.2. Виходячи з уявлень про світлові кванти, обчислити тиск рівноважного випромінювання на дзеркальну поверхню.
16.3. Обчислити енергію газу фотонів з частотами від  Гц до
Гц до  Гц при
Гц при 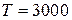 К у порожнині об’ємом 1 м3.
К у порожнині об’ємом 1 м3.
16.4. Показати, що закон випромінювання Віна  та закон випромінювання Релея–Джинса
та закон випромінювання Релея–Джинса  є частинними випадками формули Планка (16.6).
є частинними випадками формули Планка (16.6).
16.5. За якої температури густина енергії випромінювання в одноатомному газі дорівнює густині енергії газу? Обчислити температуру для випадку, коли густина газу дорівнює густині за нормальних умов.
16.6. Вивести формули для спектральної і повної густини енергії рівноважного випромінювання у двовимірному випадку.
Розділ 17
ЕЛЕМЕНТИ ТЕОРІЇ ФЛУКТУЦІЙ
Теоретичні відомості
Поняття флуктуацій та методи їх обчислення. Статистичні міркування призводять до цілком уявного висновку: у багаточастинковій системі завжди відбуваються спонтанні відхилення від рівноважного стану. При цьому показання достатньо точних приладів, при вимірюванні будь-яких термодинамічних параметрів рівноважної системи, коливатимуться з часом біля деяких середніх значень.
Отже, невпорядковані, спонтанні відхилення того чи іншого параметра від його певного рівноважного (усередненого) значення внаслідок хаотичності внутрішнього руху у багаточастинковій системі називаються флуктуаціями цього параметра (або відповідної фізичної величини).
Як правило, у макроскопічному масштабі вони майже не помітні. Однак існують явища, які пояснюються саме флуктуаціями певних параметрів: молекулярне розсіювання світла, броунівськой рух та інші. Значну роль вони відіграють у суто нерівноважних процесах, спричиняючи переходи систем у стани з більш високим порядком. Важливо також, що із загальнофізичної точки зоруфлуктуації встановлюють природну межу точності вимірювання фізичних величин.
Зараз добре відомо, що наявність флуктуацій є наслідком атомізму і хаотичності теплового руху у багаточастинкових системах. Однак теоретичні дослідження флуктуаційних явищ на початку ХХ століття (А. Ейнштейн, М. Смолуховський) були важливим етапом у розвитку фізики, оскільки призвели до усвідомлення атомістичної гіпотези, усвідомлення постулатів статистичної фізики.
Кількісна міра флуктуацій визначається у термінах середніх значень. Отже, абсолютна флуктуація величини  дорівнює
дорівнює
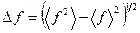 . (17.1)
. (17.1)
На мові математичної статистики це середнє квадратичне відхилення величини  від свого середнього значення
від свого середнього значення 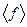 . Відносна флуктуація визначається формулою
. Відносна флуктуація визначається формулою
 . (17.2)
. (17.2)
Зрозуміло, що для обчислення флуктуацій  і
і  деякої величини, треба знати закон її розподілу.
деякої величини, треба знати закон її розподілу.
У деяких випадках корисною характеристикою пари величин  і
і  є так звана кореляція флуктуацій цих величин
є так звана кореляція флуктуацій цих величин  , яка визначається за формулою
, яка визначається за формулою
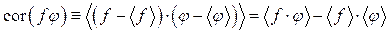 . (17.3)
. (17.3)
Розглянемо розрахунок уведених флуктуацій в межах класичного канонічного розподілу Гіббса і на прикладі внутрішньої енергії  . У цьому випадку
. У цьому випадку  , а також усі зовнішні параметри, є сталими. Позначимо середнє значення
, а також усі зовнішні параметри, є сталими. Позначимо середнє значення 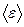 , тобто термодинамічну енергію, через
, тобто термодинамічну енергію, через  . Для розрахунку
. Для розрахунку 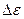 і
і 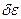 треба обчислити середні
треба обчислити середні 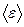 та
та  за канонічним розподілом. Маємо
за канонічним розподілом. Маємо
 , (17.4)
, (17.4)
 . (17.5)
. (17.5)
Продиференціюємо (17.4) за  . Одержимо
. Одержимо

 . (17.6)
. (17.6)
Скориставшись формулою (12.22), перепишемо (17.6) у вигляді
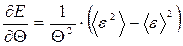 , (17.7)
, (17.7)
звідки остаточно маємо
 . (17.8)
. (17.8)
Зокрема, для одноатомного ідеального газу, коли  , одержуємо
, одержуємо
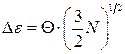 ,
,  . (17.9)
. (17.9)
У квантовому випадку з гамільтоніаном  і енергетичним спектром
і енергетичним спектром 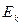 знаходимо
знаходимо
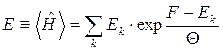 ,
,
звідки аналогічно
 .
.
Враховуючи рівняння Гіббса–Гельмгольца  , отримаємо
, отримаємо
 .
.
Отже, у квантовому випадку маємо такий самий результат, що і у класичному:
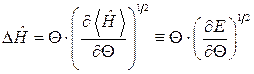 ; (17.10)
; (17.10)
тільки не завжди при цьому виконується  .
.
В деяких випадках розрахунки середніх значень викликають певні труднощі. Тому часто використовується так звана квазітермодинамічна теорія флуктуацій, яка дозволяє обчислювати ймовірності відхилень тих чи інших термодинамічних параметрів від своїх рівноважних значень. За Ейнштейном така ймовірність 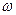 визначається відношенням кількості способів реалізації стану з відхиленням від рівноваги до кількості способів реалізації стану у рівновазі. Оскільки таке відношення пропорційне відношенню відповідних фазових об’ємів
визначається відношенням кількості способів реалізації стану з відхиленням від рівноваги до кількості способів реалізації стану у рівновазі. Оскільки таке відношення пропорційне відношенню відповідних фазових об’ємів  , з (12.6) для ізольованої системи матимемо
, з (12.6) для ізольованої системи матимемо
 . (17.11)
. (17.11)
Формула (17.11) є основною у квазітермодинамічній теорії флуктуацій.
Якщо відхилення системи від рівноважного стану характеризується одним параметром 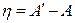 (
( – деяка термодинамічна величина), то в рівноважному стані
– деяка термодинамічна величина), то в рівноважному стані  . Розкладаючи ентропію
. Розкладаючи ентропію  нерівноважного стану у ряд за степенями
нерівноважного стану у ряд за степенями  , запишемо
, запишемо
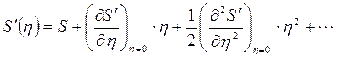 . (17.12)
. (17.12)
Враховуючи, що у рівноважному стані ентропія ізольованої системи максимальна, тобто 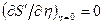 та
та 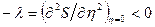 , після підстановки (17.12) у (17.11) матимемо гауссовий розподіл для малих флуктуацій (відхилень величини А)
, після підстановки (17.12) у (17.11) матимемо гауссовий розподіл для малих флуктуацій (відхилень величини А)
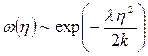 .
.
Використовуючи умову нормування, остаточно отримаємо
 . (17.13)
. (17.13)
Формулу (17.13) можна узагальнити на довільну кількість параметрів 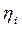 .
.
Можна також показати, що для неізольованих систем працює загальна формула
 , (17.14)
, (17.14)
де знак  позначає відхилення того чи іншого термодинамічного параметра від свого рівноважного значення, тобто
позначає відхилення того чи іншого термодинамічного параметра від свого рівноважного значення, тобто  і так далі.
і так далі.
Треба зазначити, що в деяких випадках квазітермодинамічна теорія флуктуацій призводить до розбіжностей зі статистичною теорією, яка базується на обчисленні середніх за статистичним ансамблем. Це зумовлено тим, що у першій теорії вибір змінних стану системи є довільним, у той час як у статистичній теорії флуктуацій певні параметри при заданих умовах флуктуювати за визначенням не можуть, тобто їх не можна вибирати довільно. Так, наприклад, квазітермодинамічна теорія дає 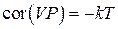 , а за статистичною теорією флуктуацій
, а за статистичною теорією флуктуацій 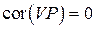 .
.
Броунівський рух. Його зв’язок з дифузією. Броунівський рух – це неперервний, хаотичний рух найдрібніших макрочастинок речовини, завислих у рідині чи газі. Це явище має чисто флуктуаційний характер і зумовлене безладними зіткненнями цих, так званих, броунівських частинок з оточуючими їх молекулами. Якою ж спостережувальною величиною можна описати броунівський рух? Зрозуміло, що це повинна бути деяка усереднена величина. Найбільш придатною з таких може бути середня відстань  , на яку відхиляється броунівська частинка за час t. Однак явний вигляд відповідного розподілу відсутній. Проте виявляється, що за його відсутності у декартових координатах досить легко обчислити саме середнє значення квадрату такої відстані:
, на яку відхиляється броунівська частинка за час t. Однак явний вигляд відповідного розподілу відсутній. Проте виявляється, що за його відсутності у декартових координатах досить легко обчислити саме середнє значення квадрату такої відстані:  . Тому з цих міркувань вибираємо як спостережувальну величину для опису броунівського руху конструкцію
. Тому з цих міркувань вибираємо як спостережувальну величину для опису броунівського руху конструкцію 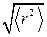 , яку не набагато складніше ніж
, яку не набагато складніше ніж  можна визначати в експерименті.
можна визначати в експерименті.
Отже, запишемо диференціальне рівняння руху броунівської частинки масою m для її координати x:
 , (17.15)
, (17.15)
де 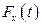 – проекція на вісь
– проекція на вісь 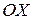 випадкової сили з боку молекул, а перший доданок у правій частині – сила в’язкого тертя. Для частинок сферичної форми
випадкової сили з боку молекул, а перший доданок у правій частині – сила в’язкого тертя. Для частинок сферичної форми  , де
, де  – їх радіус,
– їх радіус,  – коефіцієнт в’язкості середовища. Зрозуміло, що сила
– коефіцієнт в’язкості середовища. Зрозуміло, що сила 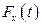 невідома. Але ж це не заважатиме розв’язанню (17.15) саме у термінах середнього
невідома. Але ж це не заважатиме розв’язанню (17.15) саме у термінах середнього  .
.
Отже, знайдемо середній квадрат зміщення  броунівської частинки від початкового її положення за час t, який набагато більший за інтервали змін випадкової сили
броунівської частинки від початкового її положення за час t, який набагато більший за інтервали змін випадкової сили  . Для цього помножимо (17.15) на x та скористаємось простими математичними рівностями
. Для цього помножимо (17.15) на x та скористаємось простими математичними рівностями
 .
.
Зробивши заміну  , (17.15) отримаємо у вигляді
, (17.15) отримаємо у вигляді
 . (17.16)
. (17.16)
Усереднимо тепер одержане рівняння за ансамблем броунівських частинок, вважаючи, що вони рухаються незалежно одна від одної. При цьому матимемо на увазі такі обставини:
1) оскільки операції усереднення і диференціювання є лінійними, їх можна переставляти, тобто  ;
;
2) кінетична енергія броунівської частинки  після усереднення (через теорему про рівнорозподіл кінетичної енергії за ступенями вільності) дорівнюватиме
після усереднення (через теорему про рівнорозподіл кінетичної енергії за ступенями вільності) дорівнюватиме  ;
;
3) інтенсивність безладних ударів з боку молекул ніяк не пов’язана з положенням частинки, тобто випадкові величини x та  є незалежними, звідки маємо
є незалежними, звідки маємо  , але ж для однорідного та ізотропного середовища
, але ж для однорідного та ізотропного середовища  .
.
Отже, після усереднення рівняння (17.16) матиме вигляд
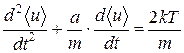 (17.17)
(17.17)
або
 , (17.18)
, (17.18)
де  . Загальний розв’язок рівняння (17.18) має вигляд
. Загальний розв’язок рівняння (17.18) має вигляд
 ,
,
звідки остаточно
 , (17.19)
, (17.19)
де  та
та  сталі інтегрування.
сталі інтегрування.
В дослідах Ж. Перрена (1908 р.) спостерігались броунівськи частинки з  10–5см,
10–5см,  10–14г у воді. У цьому випадку коефіцієнт
10–14г у воді. У цьому випадку коефіцієнт  у показнику експоненти дорівнює ~ 108 с–1, тобто при реальних проміжках часу спостерігання експоненціальним доданком у (17.19) можна знехтувати. Крім того з початкової умови
у показнику експоненти дорівнює ~ 108 с–1, тобто при реальних проміжках часу спостерігання експоненціальним доданком у (17.19) можна знехтувати. Крім того з початкової умови  при
при 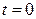 випливає, що
випливає, що  . Отже, з (17.19) отримуємо класичну формулу Ейнштейна–Смолуховського
. Отже, з (17.19) отримуємо класичну формулу Ейнштейна–Смолуховського
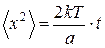 (17.20)
(17.20)
або, враховуючи рівноправність координат 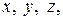
 . (17.21)
. (17.21)
Експеримент підтверджує одержану залежність середнього зміщення броунівської частинки від часу.
Розглянемо тепер зв’язок броунівського руху з дифузією. Якщо броунівськи частинки первісно були зосереджені в деякому малому об’ємі, а потім розсіялися по всьому середовищу, цей процес можна розглядати як дифузію. Встановимо зв’язок властивості середовища (коефіцієнт в’язкості  ) з характеристикою процесу дифузії (коефіцієнт дифузії
) з характеристикою процесу дифузії (коефіцієнт дифузії  ). Позначимо через
). Позначимо через  число броунівських частинок в одиниці об’єму. Розглянемо одновимірний випадок, прийнявши
число броунівських частинок в одиниці об’єму. Розглянемо одновимірний випадок, прийнявши 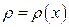 . Вилучимо уявно у товщі середовища площину
. Вилучимо уявно у товщі середовища площину 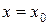 , перпендикулярну вісі OX. Позначимо через
, перпендикулярну вісі OX. Позначимо через  середнє квадратичне зміщення броунівських частинок за час t, яке визначається формулою (17.20). За цей час половина усіх частинок, що знаходяться у шарі між площинами
середнє квадратичне зміщення броунівських частинок за час t, яке визначається формулою (17.20). За цей час половина усіх частинок, що знаходяться у шарі між площинами  та
та 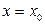 змістяться вправо по вісі OX, перетнувши площину
змістяться вправо по вісі OX, перетнувши площину  . Через одиницю площі при цьому пройде у середньому
. Через одиницю площі при цьому пройде у середньому  частинок. Аналогічно у протилежному напрямі за той же час пройде
частинок. Аналогічно у протилежному напрямі за той же час пройде 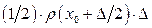 частинок. Різниця цих величин дорівнюватиме течії броунівських частинок за час t:
частинок. Різниця цих величин дорівнюватиме течії броунівських частинок за час t:
 . (17.22)
. (17.22)
Щільність течії j, тобто кількість частинок, що перетнули одиницю площі за одиницю часу, матимемо у вигляді
 ; (17.23)
; (17.23)
знак “  ”в останніх рівностях показує, що течія направлена у бік зменшення концентрації частинок.
”в останніх рівностях показує, що течія направлена у бік зменшення концентрації частинок.
Порівнюючи (17.23) з рівнянням дифузії
 ,
,
одержуємо шуканий зв'язок між величинами  і
і  :
:
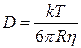 . (17.24)
. (17.24)
У свій час за допомогою співвідношення (17.24) було проведене точне вимірювання сталої Больцмана.






