Розв’язання. Число квантових станів, яке припадає на об’єм V та проміжок імпульсу dP фазового простору у перерахуванні на одну частинку дорівнює
;
в нашому випадку 
- спін електрона. Для ультрарелятивістського газу 
, що дає
.
Повне число електронів N за розподілом Фермі–Дірака запишемо у вигляді
. (1)
Газ є невиродженим за умови 
, що дозволяє знехтувати одиницею в знаменнику (1). Отже,
,
звідки після інтегрування маємо
,
де 
- густина частинок.
Температура виродження T0 визначається з рівності
,
що остаточно дає
.
Задача 7. При якій густині протонів з температурою Т= 106 К можна користуватися класичною статистикою?
Розв’язання. Вважатимемо, що класичною статистикою можна користуватися, коли 
, тобто температура виродження 
дорівнює 105 К. Температура виродження газу нерелятивістських частинок має вигляд
,
звідки маємо шукану густину n:
.
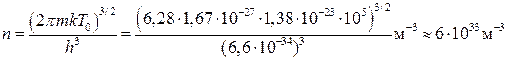Задача 8. Чому дорівнює число електронів з кінетичними енергіями від 2,0 до 2,1еВ у 1 см3 срібла при Т = 100 К ?
Розв’язання. Число електронів 
в досить вузькому інтервалі енергій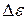 
можна знайти за формулою
, (1)
де значення 
береться з цього ж інтервалу; для електронів 
.
При 
K електронний газ в металі є сильно виродженим, і його хімічний потенціал μ не дуже відрізняється від свого значення 
при 
К. При цьому можна вирахувати (зробіть самостійно), що в нашому випадку значення 
дорівнює 
5,4·10-19 Дж, тобто показник експоненти в (1) становить
і останньою можна знехтувати у порівнянні з одиницею.
Таким чином, остаточно знаходимо
Задача 9. Одержати розподіл Фермі–Дірака за величиною швидкості для нерелятивістських електронів. Побудувати графік цього розподілу при Т = 0 К .
Розв’язання. Розподіл станів 
за імпульсами для нерелятивістського електронного газу маємо у вигляді
.
Оскільки 
, знаходимо аналогічний розподіл 
за швидкостями:
. (1)
Домноживши (1) на розподіл Фермі–Дірака середнього числа частинок 
за станами (беручи до уваги, що енергія k-го рівня 
), одержимо шуканий розподіл 
за швидкостями:
. (2)
При К(2) набирає вигляду:
, (3)
де 
- швидкість, яка відповідає енергії фермі 
.
Отже, графік (3) маємо у вигляді:
 |
Задача 10. Визначити повну енергію та теплоємність бозе-газу при температурі, що менша за його температуру конденсації.
Розв’язання. При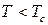 
можна знехтувати хімічним потенціалом 
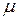бозе-газу. Тому повну енергію 
останнього можна записати як
. (1)
Заміна 
призводить (1) до вигляду
. (2)
Числове значення a інтеграла в (2) становить приблизно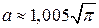 
.
Теплоємність CV знаходимо з (2):
