15.1. Визначити вільну енергію і ентропію системи з 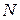 невзаємодіючих квантових лінійних осциляторів.
невзаємодіючих квантових лінійних осциляторів.
15.2. Оцінити температуру Дебая  твердого тіла і мінімальну довжину хвилі
твердого тіла і мінімальну довжину хвилі  власних коливань кристала, якщо відомі швидкість звуку
власних коливань кристала, якщо відомі швидкість звуку  у кристалі та період гратки
у кристалі та період гратки  .
.
15.3. Двохатомний квантовий ідеальний газ містить 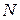 молекул, частота коливань яких
молекул, частота коливань яких  . Знайти коливальні частини вільної енергії
. Знайти коливальні частини вільної енергії  та ентропії
та ентропії 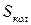 . Розглянути також граничні випадки:
. Розглянути також граничні випадки:
а) 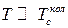 ;
;
б) 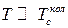 ,
,
де  – характеристична температура для коливального руху молекул.
– характеристична температура для коливального руху молекул.
15.4. За даними умови попередньої задачі знайти коливальні частини внутрішньої енергії  та ізохорної теплоємності
та ізохорної теплоємності  . Розглянути також відповідні граничні випадки.
. Розглянути також відповідні граничні випадки.
15.5. Обчислити коливальну частину  молярної теплоємності азоту при
молярної теплоємності азоту при  500 К. Частота нормальних коливань молекули
500 К. Частота нормальних коливань молекули 
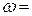
 с-1.
с-1.
15.6. Двохатомний квантовий ідеальний газ містить 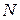 молекул, моменти інерції яких
молекул, моменти інерції яких  . Знайти обертальні частини вільної енергії
. Знайти обертальні частини вільної енергії  та ентропії
та ентропії  при
при  , де
, де  – характеристична температура для обертального руху молекул.
– характеристична температура для обертального руху молекул.
15.7. Обчислити обертальну частину  молярної теплоємності газоподібного кисню при
молярної теплоємності газоподібного кисню при  К. Момент інерції молекули
К. Момент інерції молекули 
 кг·м2.
кг·м2.
15.8. Отримати наближені значення для обертальних частин молярних теплоємностей  орто- та параводню при
орто- та параводню при  К. Момент інерції молекули
К. Момент інерції молекули 
 кг·м2.
кг·м2.
15.9. За результатами попередньої задачі обчислити обертальну частину молярної теплоємності  водню у рівноважному стані при
водню у рівноважному стані при  К. Рівноважне співвідношення молекул орто- та параводнів у природному водні
К. Рівноважне співвідношення молекул орто- та параводнів у природному водні  складає
складає  3:1.
3:1.
Розділ 16
СТАТИСТИЧНА ТЕОРІЯ РІВНОВАЖНОГО ВИПРОМІНЮВАННЯ
Теоретичні відомості
Вивчення властивостей електромагнітного випромінювання наприкінці ХІХ століття поклало початок нового – квантового погляду на усі мікроскопічні явища у природі. Саме розходження класичної теорії з експериментом у цій області фізики дозволило М. Планку у 1900 році увести фундаментальне поняття дискретності випромінювання і одержати формулу для спектральної густини енергії у стані рівноваги випромінювання з оточуючими його стінками. Втім виявилося, що випромінювання (або, інакше, газ фотонів) є завжди виродженою системою, тобто статистика випромінювання може бути тільки квантовою за будь-яких термодинамічних умов.
Отримаємо ключову формулу квантової статистики рівноважної системи фотонів для спектральної густини їх енергії. Будемо виходити з того, що імпульс  фотона дорівнює
фотона дорівнює  , а останні є бозонами зі спіном
, а останні є бозонами зі спіном  , але лише з двома спостережувальними його проекціями на напрямок руху, тобто формулу (14.21) використовуватимемо далі як
, але лише з двома спостережувальними його проекціями на напрямок руху, тобто формулу (14.21) використовуватимемо далі як
 . (16.1)
. (16.1)
Отже, за основу беремо розподіл Бозе–Ейнштейна
 , (16.2)
, (16.2)
маючи на увазі, що для фотонів хімічний потенціал 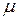 дорівнює нулю.
дорівнює нулю.
Переходячи у (16.1) до частоти  фотонів, отримаємо
фотонів, отримаємо
 , (16.3)
, (16.3)
звідки
 . (16.4)
. (16.4)
Формула (16.4) виражає середню кількість фотонів з частотами у проміжку  . Помноживши (16.4) на енергію одного фотона
. Помноживши (16.4) на енергію одного фотона 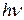 , одержимо середню енергію
, одержимо середню енергію  газу фотонів у цьому проміжку частот:
газу фотонів у цьому проміжку частот:
 . (16.5)
. (16.5)
Спектральна густина енергії  визначається як енергія фотонів в одиниці об’єму, і яка припадає на проміжок
визначається як енергія фотонів в одиниці об’єму, і яка припадає на проміжок  , тобто з (16.5) маємо
, тобто з (16.5) маємо
 . (16.6)
. (16.6)
Вираз (16.6) і є вищезгадуваною знаменитою формулою Планка – першою квантовою формулою фізичної науки. Елементарний аналіз показує, що розподіл густини енергії за частотами (16.6) є дзвонуватою кривою, яка має характерний максимум у деякій точці 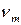 . Проінтегрувавши (16.6) за частотами (із заміною
. Проінтегрувавши (16.6) за частотами (із заміною  ), отримаємо густину енергії
), отримаємо густину енергії  рівноважного випромінювання:
рівноважного випромінювання:
 . (16.7)
. (16.7)
З урахуванням того, що останній інтеграл дорівнює  , маємо знайомий закон Стефана–Больцмана з
, маємо знайомий закон Стефана–Больцмана з  – відповідною однойменною сталою.
– відповідною однойменною сталою.
З (16.7) зразу одержуємо калоричне рівняння стану газу фотонів
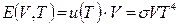 (16.8)
(16.8)
та деякі інші важливі термодинамічні характеристики:
– термічне рівняння стану
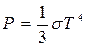 , (16.9)
, (16.9)
– ентропію
 , (16.10)
, (16.10)
– енергію Гельмгольца
 . (16.11)
. (16.11)
Пропонуємо також самостійно довести, що потенціал Гіббса рівноважного випромінювання тотожно дорівнює нулю.






