Задача 1. В яблуках сорту Ренет досліджувався вміст фруктози (х) і вітаміну С (у). Проаналізовано 9 яблук і одержано такі цифрові дані (в умовних одиницях): х – 27, 21, 18, 32, 34, 25, 22, 20, 35;
у – 50, 30, 20, 70, 80, 60, 40, 30, 70.
Питання 1. Чому дорівнює середнє арифметичне в групах х і у?
1.26 50 2. 26 ± 6,36; 50 ± 21,2.
3.26 ± 2,12; 50 ± 7,1. 4. (М ± m) х; (М ± m) у.
5. 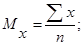
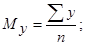
Питання 2. Як правильно записати яким є середній вміст вітаміну С в яблуках сорту Ренет (на основі проведених аналізів)?
- 50 4. 50 ± 7,1; n =9
- 50 ± 21,2 5. 50 ± 7,1
- 50; n = 9
Питання 3. Який максимальний вміст фруктози можна передбачити, з ймовірністю висновку р= 0,95, в окремому яблуці сорту Ренет?.
1. 32,36 4. 30,90
2. 38,72 5. 28,13
3. 40,60
Питання 4. Яка мінімальна межа коливання середнього вмісту вітаміну С в яблуках сорту Ренет, передбачена з ймовірністю р = 0,95?
1. Мmin = 42,9 4. Мmin = 28,8
2. Мmin = 33,7 5. Мmin = 66,3
3. Мmin = 1,2
Питання 5. Який з двох зазначених показників більш стабільний і чому?
1. Показник х, бо Сv(x) > Cv(y).
2. Показник х, бо Сv(x) < Cv(y).
3. Показник y, бо Сv(y) > Cv(x).
4. Показник y, бо Сv(y) < Cv(x).
5. Показник х, бо r = 0,5.
Питання 6. Середній вміст вітаміну С в яблуках сорту Антонівка становить 62 ± 8 (n = 9) (одиниці вимірювання ті самі).
Чи достовірне твердження, що сорт Антонівка має в середньому на 12 одиниць більший вміст вітаміну С, ніж сорт Ренет?
Відповіді:
1. Ні, бо p = 0,500 4. Ні, бо p = 0,711
2. Так, бо p = 0,500 5. Дати відповідь на це запитання неможливо.
3. Так, бо p = 0,711
Питання 7. Чи істотна різниця в мінливості між обома сортами яблук щодо вмісту вітаміну С?
Відповіді:
1. Так, бо t = 1,12 4. Ні, бо F = 1,28
2. Ні, бо t = 1,12 5. Нi, бо r = 0,64
3. Так, бо F = 1,28
Питання 8. Який коефіцієнт кореляції між вмістом фруктози (х) і вмістом вітаміну С (у) в яблуках сорту Ренет?
Відповіді:
1. 0,740 4. –0,740
2.–0,954 5. 0,954
3. 1,120
Питання 9. Яка ймовірність істотності кореляції між цими ознаками?
Відповіді:
1. p = 0,990 4. p = 0,900
2. p > 0,999 5. p < 0,900
3. p = 0,950
Питання 10. Написати рівняння лінійної регресії, за яким змінюється ознака у (вміст вітаміну С), якщо х (вміст фруктози) змінюється на одиницю.
Відповіді:
1. y = 5,22 х + 20,5 4. y = 4,50 х – 32,6
2. y = 3,18 х – 32,6 5. y = 3,18 х + 40,5
3. y = 2,46 х – 40,2
Задача 2. Досліджували вміст вітаміну А (х) і вміст заліза (у) в моркві. Зробили 10 аналізів і дістали такі цифрові дані:
х – 350, 390, 290, 280, 260, 340, 360, 280, 250, 310;
у – 18, 21, 19, 20, 16, 21, 26, 13, 18, 21.
Питання 1. Яким є середній вміст вітаміну А в моркві досліджуваного сорту?
Відповіді:
1. 311 ± 14,8 (n =10) 4. 311 ± 34,0
2. 311 ± 46,8 5. 311 ± 93,6.
3. 311 (n =10)
Питання 2. Яким є середній вміст заліза в проведеній групі аналізів?
Відповіді:
1. 19,3 ± 1,1 (n =10) 4. 19,3 ± 2,5
2. 19,3 ± 3,5 5. 19,3 ± 8,1
3. 19,3 (n =10).
Питання 3. Який з показників має більшу стабільність – вміст вітаміну А (х) чи вміст заліза (у) в моркві?
Відповіді:
1. Вітамін А, боСv(х) > Сv(у) 4. Вміст заліза, бо Сv(y) < Сv(x)
2. Вітамін А, боСv(х) < Сv(у) 5. Вміст заліза, бо Мх > My
3. Вміст заліза, бо Сv(y) > Сv(x).
Питання 4. Чи існує кореляційний зв’язок між вмістом вітаміну А і вмістом заліза в моркві? Який характер кореляції?
Відповіді:
1. Кореляція позитивна, ׀ r ׀ = 0,71.
2. Кореляція негативна, ׀ r ׀ = 0,71.
3. Кореляція позитивна, ׀ r ׀ = 1,70.
4. Кореляція негативна, ׀ r ׀ = 1,70.
5. Кореляція негативна, ׀ r ׀ = 0,56.
Питання 5. Яка ймовірність р, що одержаний кореляційний зв’язок статистично достовірний?
Відповіді:
1. р = 0,99, бо z = 1,25 4. р = 0,90, бо z = 0,68
2. р = 0,96, бо z = 0,91 5. р = 0,99, бо z = 1,25
3. р = 0,999, бо z = 1,75.
Питання 6. Який діапазон індивідуальних коливань вмісту А в моркві даного сорту, статистично достовірний з ймовірністю р = 0,95?
Відповіді:
1. 311 ± 10,7 4. 311 ± 46,8
2. 311 ± 14,8 5. 311 ± 107,6
3. 311 ± 34,0
Питання 7. Який діапазон коливань середнього вмісту заліза в моркві даного сорту, якщо ймовірність висновку р = 0,95?
Відповіді:
1. 19,3 ± 10 4. 19,3 ± 8,1
2. 19,3 ± 2,5 5. 19,3 ± 3,5
3. 19,3 ± 1,1.
Питання 8. Яким стане діапазон коливань середнього вмісту заліза в моркві, якщо висновок потрібно зробити з ймовірністю р = 0,99?
Відповіді:
1. 19,3 ± 3,6 4. 19,3 ± 11,6
2. 19,3 ± 3,9 5. 19,3 ± 8,1
3. 19,3 ± 2,5
Питання 9. Згідно з літературними даними (nліт = 10), для того самого сорту моркви вміст вітаміну А становить 300 ± 12, а вміст заліза – 29 ± 1,3 (одиниці вимірів ті самі). Чи достовірна різниця у вмісті заліза в моркві між нашими і літературними даними?
Відповіді:
1. Так, бо t = 5,7. а це відповідає ймовірності твердження р > 0,999
2. Ні, бо t = 5,7, р = 0,55
3. Так, бо t = 1,0, р = 0,66
4. Ні, бо t = 2,0, р = 0,92
5. Так, бо t = 2,0, р = 0,95.
Питання 10. Чи суперечать наші дані щодо вмісту вітаміну А в моркві літературним?
Відповіді:
1. Так, бо ймовірність різниці середніх значень р = 0,90.
2. Ні, бо р = 0,90
3. Так, бо р = 0,58
4. Ні, бо р = 0,58
5. Так, бо р = 0,95.
Задача 3. Досліджувався вміст у крові токоферолу (х) та холестерину (у). На основі 10 проведених аналізів отримано такі дані (в умовних одиницях):
х:0,69, 0,83, 0,84, 0,76, 0,95, 0,67, 0,87, 0,65, 0,72, 0,79;
у: 170, 185, 185, 175, 190, 170, 185, 165, 175, 180.
Варіант А
Питання 1. Як правильно записати висновок про середній вміст у крові токоферолу (х)? Ймовірність висновку р =0,99.
Відповіді:
1. 0,78 4. 0,78 ± 0,10
2. 0,78 ± 0,07 5. 0,78 ± 0,05
3. 0,78 ± 0,03
Питання 2. Яким може бути найбільше середнє значення токоферолу в крові, якщо задатися ймовірністю висновку р =0,95?
Відповіді:
1. 0,81 4. 0,78
2. 0,71 5. 0,90
3. 0,85
Питання 3. Прийнявши величину ймовірності висновку р =0,999, встановити в якому інтервалі будуть коливатися поодинокі значення вмісту токоферолу в крові.
Відповіді:
1. 0,33 – 1,23 4. 0,65 – 0,91
2. 0,71 – 0,85 5. 0,60 – 1,10
3. 0,55 – 1,00
Питання 4. Який із досліджуваних показників – вміст токоферолу (х) чи вміст холестерину (у) характеризується більшою стабільністю і чому?
Відповіді:
І. Вміст токоферолу, боСv(х) < Сv(у)
2. Вміст токоферолу, боСv(x > Сv(y).
3. Вміст холестерину, бо Сv(y)< Сv(x)
4. Вміст холестерину, бо Сv(у)> Cv(x)
5. Сv(х) = Cv(у)
Питання 5. За літературними даними вміст токоферолу становить 0,85 ± 0,095 (умовних одиниць) при n =10. Чи достовірне твердження, що різниця між нашими і літературними даними є статистично істотною?
Відповіді:
1. Різниця достовірна, бо ймовірність цього твердження р > 0,95
2. Різниця не достовірна, бо ймовірність цього твердження р < 0,50.
3. Різниця достовірна, оскільки проведено достатню кількість дослідів.
4. Різниця не достовірна, оскільки кількість дослідів є надто малою.
Питання 6. Яким коефіцієнтом і якою таблицею слід користуватися, досліджуючи питання про статистичну істотність за мінливістю вмісту токоферолу в крові між нашими і літературними даними? Чи істотна ця різниця?
Відповіді:
І. Коефіцієнтом і таблицею Стьюдента. Різниця істотна.
2. Коефіцієнтом і таблицею Стьюдента. Різниця не істотна.
3. Коефіцієнтом і таблицею Фішера. Різниця істотна.
4. Коефіцієнтом і таблицею Фішера. Різниця не істотна.
Питання 7. Яким коефіцієнтом кореляції характеризується зв’язок між вмістом токоферолу і холестерину в крові?
Відповіді:
І.. r = –0,53 3. r= – 1,01
2. r =- –0,97 4. r = 0,97
Питання 8. Яка ймовірність істотності кореляційногозв’язку між ознаками х і у?
Відповіді:
І. р=0,97 3. р >0,999
2. р >0,95 4. р <0,50
Питання 9. Як слід досліджувати ймовірністьтвердження про статистичнуістотність кореляції?
Відповіді:
І. Переводом r в z
2. Переводом r в z і обчисленням коефіцієнта Стьюдента.
3. Обчисленням критерію Пірсона χ2.
4. Доказом твердження про нормальний тип розподілу.
Питання 10. Якщо б було одержано при розрахунках значення r =1,5, то чи свідчило б це про більш тісний взаємозв'язок між показниками х і у?
Відповіді:
І. Більш тісний взаємозв’язок між показниками, ніж при r =1.
2. Надто велику кількість проведених дослідів.
3. Арифметичну помилку при обчисленні коефіцієнта кореляції.
4. Велику достовірність кореляційного зв'язку.
Варіант В
Питання 1. Як правильно записати висновок про середній вміст у крові холестерину(у)? Ймовірність висновку р =0,99.
Відповіді:
І. І78 ± 2,6. 3.178 ± 8,6
2. 178 4.178 ± 6,0
Питання 2. Яким може бути найменше середнє значення холестерину в крові, якщо задатися ймовірністю висновку р =0,95?
Відповіді:
І. 172 3. 178
2.184 4. 176,4
Питання 3. Прийнявши величину ймовірності висновку р =0,999, встановити в якому інтервалі будуть коливатися поодинокі значення вмісту холестерину в крові.
Відповіді:
І. 166 – 190 3. 157 – 197
2. 172 – 184 4. 140 – 216
Питання 4. Який із досліджуваних показників, вміст токоферолу (х) чи вміст
холестерину(у), характеризується більшою стабільністю і чому?
Відповіді:
І. Вміст токоферолу, боСv(х) > Сv(у)
2. Вміст токоферолу, боСv(x < Сv(y).
3. Вміст холестерину, бо Сv(y) > Сv(x)
4. Вміст холестерину, бо Сv(у) < Cv(x)
5. Сv(х) = Cv(у)
Питання 5. За літературними даними вміст холестерину становить І70,0 ± 1,2 (умовних одиниць) при n =10. Чи достовірне твердження, що різниця між нашими і літературними даними є статистично істотною?
Відповіді:
1. Різниця достовірна, бо ймовірність цього твердження р > 0,95
2. Різниця не достовірна, бо ймовірність цього твердження р < 0,50.
3. Різниця достовірна, оскільки проведено достатню кількість дослідів.
4. Різниця не достовірна, оскільки кількість дослідів є надто малою.
Питання 6. Яким коефіцієнтом і якою таблицею слід користуватися досліджуючи питання про статистичну істототність різниці за мінливістю вмісту холестерину в крові між нашими і літературними даними? Чи істотна ця різниця?
Відповіді:
І. Коефіцієнтом і таблицею Стьюдента. Різниця істотна.
2. Коефіцієнтом і таблицею Стьюдента. Різниця не істотна.
3. Коефіцієнтом і таблицею Фішера. Різниця істотна.
4. Коефіцієнтом і таблицею Фішера. Різниця не істотна.
Питання 7. Яким коефіцієнтом кореляції характеризується зв’язок між вмістом холестерину і токоферолу в крові?
Відповіді:
І.. r = –0,53 3. r= – 1,01
2. r =- –0,97 4. r = 0,97
Питання 8. Яка ймовірність істотності кореляційного зв’язку між ознаками х і у?
Відповіді:
І. р=0,971 3. р >0,999
2. р >0,95 4. р <0,50
Питання 9. Як слід досліджувати ймовірність твердження простатистичну істотність кореляції?
Відповіді:
І. Переводом r в z
2. Переводом r в z і обчисленням коефіцієнта Стьюдента.
3. Обчисленням критерію Пірсона χ2.
4. Порівнянням коефіцієнтів варіації обох показників.
Питання 10. Якщо б було одержано при розрахунках значення r =2,7, то чи свідчило б це про більшу тісноту взаємозв’язкуміж показниками х і у?
Відповіді:
І. Взаємозв’язок між показниками більший, ніж при r =1.
2. Достовірність кореляції є більшою, ніж 0,95.
3. Для відповіді на поставлене питання слід продовжити досліди.
4. При обчисленні коефіцієнта кореляції допущено арифметичну помилку
Задача 4. Проведено 100 аналізів на вміст свинцю в печінці при захворюванні А. Дістали такі цифрові дані:
| Класи | 31 – 40 | 41 – 50 | 51 – 60 | 61 –70 | 71 – 80 |
| Частота (f) |
Питання 1. Який з цих класів модальний і яким є класовий інтервал h?
Відповіді:
1. 51 – 60, h = 104. 61 – 70, h = 10
2. 31 – 40, h = 10 5. 71 – 80, h = 10
3. 51 – 60, h = 9
Питання 2. Чому дорівнює середнє арифметичне і середнє квадратичне відхилення для проведеної групи аналізів?
Відповіді:
1. М = 55,5; σ = 1,89 4. М = 54,2; σ = 9,5
2. М = 54,5; σ = 0,95 5. М = 56,8; σ = 9,5
3. М = 55,5; σ = 9,5.
Питання 3. Який середній вміст свинцю в печінці при захворюванні А?
Відповіді:
1. 55,5 4. 54,2
2. 54,2 ± 9,50 5. 55,5 ± 0,89
3. 54,2 ± 0,95
Питання 4. Який найбільший середній вміст свинцю можна передбачити в печінці при захворюванні А? Достовірність висновку р = 0,99.
Відповіді:
1. 78,8 4. 57,0
2. 56,7 5. 63,6
3. 56,1
Питання 5. Який найменший вміст свинцю можна передбачити в печінці поодинокого хворого захворюванням А? Достовірність висновку р = 0,95.
Відповіді:
1.52,3 4. 53,3
2.35,6 5. 44,8
3.52,0
Питання 6. Ч є достовірною підстава вважати (з р > 0,95), що розподіл частот в таблиці вихідних даних підлягає закону 1:2:4:2:1?
Відповіді:
1. Так, бо χ2 = 8,45 > 7,81
2. Так, бо χ2 = 8,45 < 9,49
3. Ні, бо χ2 = 8,45 < 11,07
4. Ні, бо χ2 = 5,10 < 11,07
5. Ні, бо χ2 = 5,10 < 9,49
Питання 7. Між вмістом свинцю в печінці і легенях при захворюванні А існує позитивна кореляція r = 0,785, встановлена на матеріалі 52 аналізів. Чи можна вважати цей зв’язок статистично достовірним?
- Так, бо його достовірність р = 0,95
- Ні, бо р <0,95
- Ні, бо р = 0,90
- Так, бо р >0,99
- Так, бо p = 0,99
Питання 8. Середній вміст свинцю в легенях при захворюванні А виявився рівнем 77,6 ± 2,3 (n=100). Який з двох досліджуваних органів проявив більшу статистичну стабільність щодо концентрації свинцю?
1. Легені, бо Сv= 29,8%
2. Печінка, бо Сv=17,5%
3. Легені, бо r =0,785
4. Печінка, бо r =0,785
4. Одержані дані не дозволяють відповісти на це запитання
Питання 9. Скласти рівняння регресії для залежності концентрації свинцю в легенях (у) від концентрації його в печінці (х)?
Відповіді:
1. y = 0,785х + 37,2 4. y = 0,785 х – 37,2
2. y = 1,92 х – 94,8 5. y = 1,92 х – 26,5
3. y = 1,92 х + 26,5
Питання 8. При захворюванні В середній вміст свинцю в печінці становив 65 ± 1,12 одиниць (n = 50).
Чи достовірна різниця в середньому вмісті свинцю в печінці для захворюван-ня А і В?
Відповіді:
1. Так, бо р = 0,97
2. Ні, бо р < 0,95
3. Так, бо р > 0,99
4. Ні, бо р = 0,90
5. Так, бо р = 0,95.
Задача 5. Відомо, що куріння (ознака х) сприяє появі раку легенів (ознака у). У типовому місті країни А серед робітників однієї професії віком від 40 до 50 років були проведені обстеження частоти захворювання на рак легенів у осіб, які курили (+), і у осіб, які не курили (–). Всього обстежено 25 осіб і одержано такі дані (в частотах випадків):
| у х | + | – | Всього |
| + | |||
| – | |||
| Всього |
Паралельні обстеження групи 1000 осіб, які курили, у віці від 50 до 60 років показали, що середній процент захворювання на рак легенів для цієї вікової категорії становить 10,5 ± 1,0 (%).
Питання 1. Який процент захворювання на рак легенів був зареєстрований при обстеженні всієї групи осіб у віці від 40 до 50 років?
Відповіді:
1. 7,8 4. 4,4
2. 96,0 5. 54,0
3. 1,9
Питання 2. Як правильно записати висновок про середній процент захворювання раком легенів осіб, що курять в віці від 40 до 50 років, якщо задатися ймовірністю висновку р = 0,95?
Відповіді:
1. 7,8 ± 0,3 4. 4,0 ± 0,8
2. 7,8 ± 0,9 5. 4,0
3. 4,0 ± 0,4
Питання 3. Прийнявши величину ймовірності висновку р = 0,95, встановити в якому інтервалі, в середньому, коливається процент захворювання раком легенів осіб, що курять у віці від 50 до 60 років?
Відповіді:
1. 2,5 – 11,5 4. 7,2 – 13,8
2. 8,5 – 12,5 5.
3. 8,0 – 13,0
Питання 4. Яка різниця в процентах захворювання раком легенів між особами, що курять і особами, які не курять?
Відповіді:
1. 5,9 4. 2,1
2. 3,8 5.
3. 2,7
Питання 5. Яка ймовірність твердження, що дана різниця є статистично істотною (достовірною)? Яка стандартна похибка цієї різниці?
Відповіді:
1. Різниця достовірна, бо ймовірність твердження р = 0,95, md = 1,1.
2. Різниця достовірна, бо ймовірність твердження р > 0,999, md = 1,1.
3. Різниця достовірна, бо ймовірність твердження р > 0,999, md = 0,8.
4. Різниця достовірна, бо ймовірність твердження р < 0,50, md = 0,8.
5. Різниця достовірна, бо ймовірність твердження р = 0,95, md = 0,8.
Питання 6. На скільки збільшується, в середньому, процент захворювання на рак легенів у віці 50-60 років у порівнянні з віком 40-50 років, у осіб, які курять?
Відповіді:
1. 2,7 4. 2,1
2. 3,8 5.
3. 5,9
Питання 7. Який коефіцієнт потрібно обчислити, щоб встановити, чи дане збільшення є статистично достовірним. Яка величина цього коефіцієнта?
Відповіді:
1. Коефіцієнт Стьюдента, t = 7,4.
2. Коефіцієнт Фішера, F = 1,3.
3. Коефіцієнт Фішера, F = 2,5.
4. Коефіцієнт Стьюдента, t = 2,1.
Питання 8. Яка ймовірність висновку, що різниця в частоті захворювання на рак легенів у двох обстежених вікових групах є статистично достовірною?
Відповіді:
І. р = 0,95 4. р < 0,50
2. р > 0,95 5. р = 0,99
3. р > 0,999
Питання 9. Чи існує кореляційний зв’язок між курінням і захворюванням на рак легенів? Який характер кореляційного зв’язку і яка величина коефіцієнта кореляції?
Відповіді:
1. Кореляція негативна, r = –0,14.
2. Кореляція позитивна, r = 0,14.
3. Кореляція позитивна, r = 0,29.
4. Кореляція негативна, r = –0,29.
5. Кореляційний зв’язок не встановлений.
Питання 10. Чи можна вважати, що кореляція між захворюванням на рак легенів і курінням є доведена в даних обстеженнях з достатньою ймовірністю? Як слід досліджувати ймовірність істотності кореляційного зв’язку при альтернативній класифікації експериментальних даних?
Відповіді:
І. р = 0,95; переводом r в z і обчисленням коефіцієнта Стьюдента t.
2. р > 0,999; переводом r в z і обчисленням коефіцієнта Стьюдента t.
3. р = 0,99; переводом r в z і обчисленням коефіцієнта Стьюдента t.
4. р = 0,95; обчисленням критерію Пірсона χ2.
5. р > 0,999; обчисленням критерію Пірсона χ2
КОНТРОЛЬНА РОБОТА
Досліджувався вміст хлорофілу (x) та йоду (у) у водоростей виду А на глибині 1 м. На основі проведених аналізів (n = 10) отримано такі дані в умовних одиницях – x: 65, 81, 94, 51, 74, 60, 78, 68, 74, 65; y: 4, 29, 31, 11, 18, 25, 21, 30, 27, 19.
Питання 1. Вирахуйте середнє арифметичне значення вмісту хлорофілу для
обстеженої групи водоростей.
Питання 2. Вкажіть правильну форму запису висновку про середній вміст хлорофілу у водоростей на глибині 1 м на основі проведених 10 аналізів.
Питання 3. Обчисліть середнє квадратичне відхилення для групи аналізів хлорофілу (x).
Питання 4. Обчисліть значення дисперсії (варіанти) для групи аналізів йоду (y).
Питання 5. Виходячи з одержаних даних, зробити висновок з імовірністю р = 0,95 про те, який може бути максимальний вміст йоду в окремої водорості на глибині 1 м.
Питання 6. Встановити з імовірністю р = 0,99, в якому діапазоні коливається значення середнього вмісту йоду у водоростей досліджуваного виду (в генеральній сукупності).
Питання 7. Який з двох вказаних показників (x,y) характеризується більшою стабільністю і чому?
Питання 8. Середній вміст хлорофілу у водоросгей на глибині 10 м (за даними суміжної лабораторії) становить 78,4 ± 1,93 умовних одиниць. Вирахуйте коефіцієнт Стьюдента для різниці між середнім значенням вмісту хлорофілу на вказаних двох різних глибинах.
Питання 9. Чи різниця між середнім вмістом хлорофілу у водоростей на глибині 1-го та 10-ти метрів може вважатися статистично достовірною і чому?
Питання 10. Чи можна стверджувати з ймовірністю р = 0,95, що між вмістом хлорофілу у водоростей на різній глибині (1-го та 10-ти метрів) існує статистично істотна різниця по величині мінливості і який статис-тичний показник треба застосувати для відповіді на це питання?
Питання 11. Обчисліть коефіцієнт кореляції між вмістом хлорофілу (x) і вмістом йоду (y) у досліджуваних водоростей на глибині 1 м.
Питання 12. Яким є характер встановленого нами кореляційного зв’язку?
Питання 13. Переведіть одержане значення коефіцієнта кореляції r в показник z і обчисліть для нього коефіцієнт Студента t необхідний для оцінки істотності твердження про кореляцію.
Питання 14. З якою ймовірністю, можна стверджувати, що одержане значення коефіцієнта кореляцїї є статистично істотне?
Питання 15. Вкажіть граничне значення коефіцієнта кореляції для даної серії
досліджень, при якому істотність твердження про кореляцію має ймовірність 0,95.
Питання 16. Вкажіть формулу зв'язку між коефіцієнтом кореляції r і коефіцієнтом регресії by/x, який показує на залежність зміни середнього вмісту йоду (y) від вмісту хлорофілу (x) у досліджуванихводоростей.
Питання 17. Обчисліть коефіцієнт лінійної регресії by/x длязміни середнього вмісту йоду (y) в залежності від вмісту хлорофілу (x).
Питання 18. Виведіть рівняння лінійної регресії, яке показує, як змінюється вміст йоду (y) в залежності від вмісту хлорофілу (x) у досліджуваних водоростей.
Питання 19. Користуючись виведеним рівнянням, обчисліть, який вміст йоду відповідає, в середньому, вмісту хлорофілу x = 70 для досліджуваних водоростей на глибині 1 м.
Питання 20. Вирахуйте коефіцієнт лінійної регресії bx/удля зміни середнього вмісту хлорофілу (x) в залежності від зміни вмісту йоду (y).






