На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии  . На плоскость наудачу брошена игла длины
. На плоскость наудачу брошена игла длины 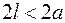 . Какова вероятность того, что игла пересечёт какую-нибудь прямую?
. Какова вероятность того, что игла пересечёт какую-нибудь прямую?
 |
Решение.
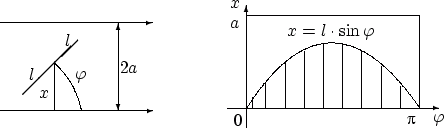
Рис. 7.18
Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причём две эти переменные (положение центра и угол поворота) меняются независимо друг от друга. Обозначим через  расстояние от середины иглы до ближайшей прямой, а через
расстояние от середины иглы до ближайшей прямой, а через  — угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника
— угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника 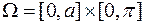 .
.
Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству:  . Площадь области
. Площадь области  , точки которой удовлетворяют такому неравенству, равна
, точки которой удовлетворяют такому неравенству, равна
 .
.
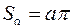 .
.
Тогда
 .
.
Ответ:  .
.
Задача 41. Монета упала на дощатый пол. Ширина доски  , радиус монеты
, радиус монеты 
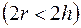 . Какова вероятность того, что монета попадет на щель?
. Какова вероятность того, что монета попадет на щель?
Решение. Пусть 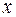 – координаты центра монеты – расстояние от края доски до монеты.
– координаты центра монеты – расстояние от края доски до монеты.
Пространств элементарных событий  ,
, 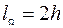 .
.
Событие 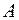 состоит в перекрытии щели монетой.
состоит в перекрытии щели монетой.
 ,
,  .
.
Вероятность появления события 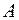 равна:
равна:
 .
.
Ответ:  .
.
Задача 42. Из отрезка [0, 2] на удачу выбраны два числа 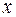 и
и 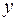 . Найдите вероятность того, что эти числа удовлетворяют неравенствам
. Найдите вероятность того, что эти числа удовлетворяют неравенствам  .
.
Решение.
 |
Рис. 7.19
По условиям опыта координаты точки  удовлетворяют системе неравенств:
удовлетворяют системе неравенств:  Это значит, что точка
Это значит, что точка  наудачу выбирается из множества точек квадрата со стороной 2. Интересующее нас событие происходит в том и только в том случае, когда выбранная точка
наудачу выбирается из множества точек квадрата со стороной 2. Интересующее нас событие происходит в том и только в том случае, когда выбранная точка  окажется под прямой и над параболой (рис. 7.19). Эта область получена как множество точек, ординаты которых удовлетворяют неравенствам
окажется под прямой и над параболой (рис. 7.19). Эта область получена как множество точек, ординаты которых удовлетворяют неравенствам  . Следовательно, искомая вероятность равна отношению площади области к площади квадрата:
. Следовательно, искомая вероятность равна отношению площади области к площади квадрата:
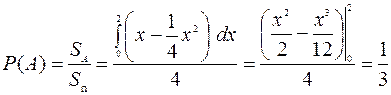 .
.
Ответ: 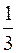 .
.
Задача 43. Наудачу взяты два положительных числа 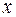 и
и 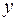 , каждое из которых не превышает двух. Найти вероятность того, что произведение
, каждое из которых не превышает двух. Найти вероятность того, что произведение  будет не больше единицы, а частное
будет не больше единицы, а частное  не больше двух.
не больше двух.
 Решение. По условиям опыта координаты точки
Решение. По условиям опыта координаты точки  удовлетворяют системе неравенств:
удовлетворяют системе неравенств:
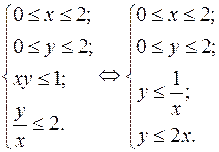
Область, благоприятствующая появлению события изображена на рис. 7.20.
Рис. 7.20
 ,
,

Тогда
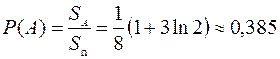 .
.
Ответ:  .
.
Задача 44. Доказать свойства С 3 – С 10.
Доказательство.
С 3. Нужно доказать, что для любого события 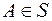 :
: 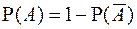 .
.
Так как  , и события
, и события 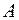 и
и  несовместные, то из аксиомы А2 и свойства С 2 получаем:
несовместные, то из аксиомы А2 и свойства С 2 получаем:

откуда 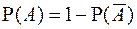 .
.
С. 4 Докажем, что если A⊆B, то 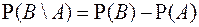 .
.
Представим B, в виде суммы двух несовместных событий:  . По свойству С 2 получаем
. По свойству С 2 получаем  , откуда выражая
, откуда выражая 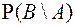 получаем требуемое.
получаем требуемое.
С. 5 Докажем свойство монотонности вероятности. (Если A⊆B, то 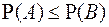 ).
).
В доказательстве предыдущего свойства было получено 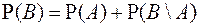 . Но так как в силу аксиомы неотрицательности А1
. Но так как в силу аксиомы неотрицательности А1  , то
, то  ч.т.д.
ч.т.д.
С 6. Требуется доказать, что  .
.
По А1  . Но так как
. Но так как 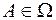 , то по свойству С 5
, то по свойству С 5  откуда и получаем, что
откуда и получаем, что  .
.
С 7. Докажем, что 
 , следовательно, по свойству С 2
, следовательно, по свойству С 2  .
.
Так как слагаемое  , то
, то  , что сразу доказывает свойство С 8.
, что сразу доказывает свойство С 8.
С 9. Покажем, что всегда выполняется
 .
.
Так как  , где
, где  . А так как события
. А так как события  и
и  несовместны, то
несовместны, то
 .
.
Для доказательства свойства С 10: для любого конечного набора событий  имеет место равенство (6.1)
имеет место равенство (6.1)
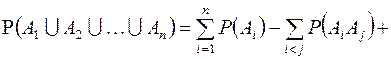
 ,
,
воспользуемся методом математической индукции. При  утверждение верно (свойство С 7.) Предположим, что утверждение верно для произвольных
утверждение верно (свойство С 7.) Предположим, что утверждение верно для произвольных  событий
событий 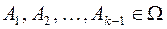 . Докажем, что оно верно для
. Докажем, что оно верно для 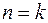 . По свойству С 7
. По свойству С 7
 (7.1)
(7.1)
По предположению индукции первое слагаемое в правой части (7.1) равно

 (7.2)
(7.2)
Вычитаемое в правой части (7.1) равно
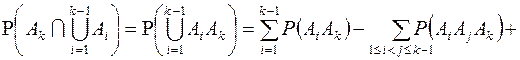
 (7.3)
(7.3)
Подставляя (7.2) и (7.3) в (7.1) получим




 .
.
ч.т.д.






