ПОНЯТИЕ
«ВЕРОЯТНОСТЬ»
Учебное пособие
Самара
Самарский государственный технический университет
Печатается по решению Редакционно-издательского совета СамГТУ
УДК 519.2
Р е ц е н з е н т: канд. физ.-мат. наук И.С. Пулькин
Евдокимов М.А., Бейлина Н.В
Понятие вероятность: учеб.пособ. / М.А. Евдокимов, Н.В. Бейлина. – Самара. Самар.гос.техн.ун-т, 2011. – 68 с.: ил.
ISBN
Изложенный материал соответствует рабочей программе по курсу теория вероятностей для студентов всех инженерно-технических специальностей СамГТУ.
Содержит теоретические сведения и методические указания, примеры решения задач, а также задачи для самостоятельного решения.
Предназначено для студентов и преподавателей университета.
УДК 519.2
ISBN Ó М.А. Евдокимов, Н.В. Бейлина, 2011
Ó Самарский государственный
технический университет, 2011
ОСНОВНЫЕ ПОНЯТИЯ
Теория вероятностей как раздел математики изучает математические модели случайных явлений, т.е. модели экспериментов, единичные исходы которых невозможно однозначно предсказать, учитывая условия проведения эксперимента. Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях. В теории вероятностей неопределяемым понятием является «случайное событие» или просто «событие».
Для математического описания экспериментов со случайными исходами нам потребуется прежде всего понятие пространства элементарных исходов (или событий), соответствующее рассматриваемому эксперименту.
Определение 1.1. Пространством элементарных исходов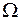 
называется множество взаимоисключающих исходов эксперимента, такое что каждый интересующий нас результат эксперимента может быть однозначно записан с помощью элементов этого множества. Элементы этого множества называют элементарными исходами и обозначают буквой 
(
).
Определение 1.2. Событиями будем называть подмножества множества 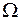. Говорят, что в результате эксперимента произошло событие 
, если в эксперименте произошел один из элементарных исходов, входящих в множество 
.
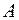Замечание. Вообще говоря, можно назвать событиями не обязательно любые подмножества множества 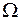, а лишь элементы некоторого набора подмножеств.
Пример 1.1. Игральная кость подбрасывается один раз. Пространство элементарных исходов Ω = {1, 2, 3, 4, 5, 6}, элементарные исходы здесь соответствуют числу выпавших очков.
Примеры событий:
A = {1, 2} — выпало одно или два очка;
B = {1, 3, 5} — выпало нечётное число очков.
C = {3,6} – выпало число очков, кратное 3.
Пример 1.2. Один раз подбрасываются две игральные кости. Будем считать пространством элементарных исходов множество пар чисел 
, где 
(соответственно, 
) есть число очков, выпавших при первом (втором) подбрасывании: 
.
Примеры событий:
А = {(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1)} — на второй кости выпало одно очко;
В = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)} — на костях выпало одинаковое число очков;
С = {(2, 2), (2,4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)} — на обеих костях выпало чётное число очков.
Несколько событий образуют полную группу, если в результате испытания появится одно из них.
Пример 1.3. Образуют ли полную группу следующие группы событий:
a) Опыт – бросание двух монет; события:
А1 = {появление двух гербов};
А2 = {появление двух цифр}.
b) Опыт – два выстрела по мишени; события:
В1 = {ни одного попадания};
В2 = {одно попадание};
В3 = {два попадания}.
Ответ: а) нет; b) да.
Виды случайных событий
События можно подразделить на четыре вида: достоверные, невозможные, несовместные и случайные.
Определение 1.3. Событие называется достоверным, если оно обязательно произойдёт в результате опыта, т.е. единственное событие, включающее все элементарные исходы — Ω.
Пример 1.4. Из ящика с черными и белыми шарами наудачу извлечен шар. События А — «появился шар» является достоверным.
Определение 1.4. Невозможным называется событие, которое заведомо не произойдёт в результате опыта, т. е. событие, не содержащее ни одного элементарного исхода («пустое множество» Æ). Заметим, что всегда Æ⊂Ω.
Пример 1.5. В урне белые и черные шары. Событие А — извлечение из этой урны красного шара. Событие А — невозможное.
Определение 1.5. Случайным называют событие, которое в результате опыта может либо произойти, либо не произойти.
Пример 1.6. Выпадение решки при подбрасывании монеты.
Определение 1.6. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пример 1.7. Из ящика с черными и белыми шарами наудачу извлечен шар. Появление белого шара исключает появление черного шара. События А — «появился белый шар» и В — «появился черный шар» являются несовместными.
Пример 1.8. Брошена монета. Появление герба исключает появление решки. События «появился герб» и «появилась решка» — несовместные.
Операции над событиями
В теории вероятностей существуют те же операции над событиями, что и в теории множеств над множествами.
Определение 1.7. Суммой (объединением) событий А и В называется событие А+В (A∪B), состоящее в том, что произошло либо A, либо B, либо оба события одновременно (т. е. хотя бы одноиз событий А или В).
 |
Рис. 1.1
На языке теории множеств A∪B есть множество, содержащее как элементарные исходы из множества A, так и элементарные исходы из множества B (рис. 1.1).
Определение 1.8. Произведением (пересечением) АВ (A∩B) событий A и B называется событие, состоящее в том, что произошли оба события A и B одновременно.
 |
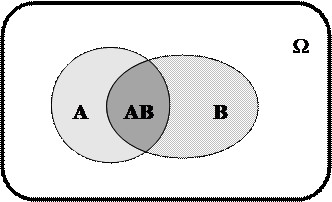На языке теории множеств A∩B есть множество, содержащее элементарные исходы, входящие в пересечение множеств A и B (рис. 1.2).
Рис. 1.2
Определение 1.9. Разностью событий А\В (дополнением события В до А) называется событие, которое в результате опыта имеет место, если происходит событие А и не происходит событие В.
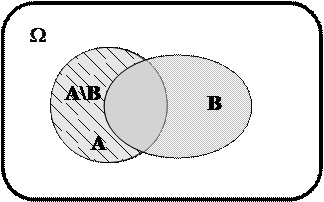
То есть множество A\B содержит элементарные исходы, входящие в множество A, но не входящие в B (рис. 1.3).
Рис. 1.3
 |
Определение 1.10. Противоположным (дополнительным) к событию A называется событие
= Ω\A, состоящее в том, что событие A в результате эксперимента не произошло. Т.е. множество A состоит из элементарных исходов, не входящих в A (рис. 1.4).Рис. 1.4
Определение 1.11. Говорят, что событие A влечет событие B, и пишут A⊆B, если всегда, как только происходит событие A, происходит и событие B.
На языке теории множеств это означает, что любой элементарный исход, входящий в множество A, одновременно входит и в множество B, т.е. A содержится в B (рис. 1.5).
 |
Рис 1.5
ВЕРОЯТНОСТЬ НА ДИСКРЕТНОМ ПРОСТРАНСТВЕ ЭЛЕМЕНТАРНЫХ СОБЫТИЙ
Обозначим через Ω множество взаимоисключающих исходов эксперимента 
, 
, …, 
(элементарных событий): 
.
Определение 2.1. Пространство элементарных исходов называется дискретным, если оно конечно или счетно: 
.
Замечание. Множество конечно, если оно состоит из конечного числа элементов. Множество счетно, если существует взаимно-однозначное соответствие между этим множеством и множеством всех натуральных чисел. Счётными множествами являются множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество нечётных (четных) чисел и т. д.
Определение 2.2. Вероятностным пространством называется не более чем счетное (дискретное) множество , каждому элементу которого поставлено в соответствие число 
, называемое вероятностью элементарного события.
Таким образом, вероятностное пространство — это пара объектов {Ω;P}.
Чтобы определить вероятность любого события на дискретном пространстве элементарных исходов, достаточно присвоить вероятность каждому элементарному исходу. Тогда вероятность любого события определяется как сумма вероятностей входящих в него элементарных исходов.
Определение 2.3. Поставим каждому элементарному исходу 
в соответствие число 
так, что
.
Назовём число 
вероятностью элементарного исхода 
. Вероятностью события A назовём число 
, равное сумме вероятностей элементарных исходов, входящих в множество A. В случае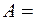 
Æ положим 
.
Итак, в вероятностном пространстве элементарные события выступают как неделимые «атомы», из которых строятся более сложные конструкции — события.
Пример 2.1. Подбрасывают монету. В данном случае пространство элементарных событий состоит из двух элементарных событий 
и 
(выпадение герба и выпадение решки).
Согласно определению 2.2 на множестве Ω задана функция 
— вероятность. Очевидно, что нужно положить 
.
Пример 2.2. Рассмотрим бросание игральной кости. В этом случае 
, 
— выпадение на кости очков. Можно строить различные события: 
– выпало нечётное число очков, 
– выпало число очков, кратное 3 и т.д. Ясно, что для симметричной игральной кости 
.
Тогда
.
.
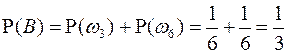Если пространство элементарных исходов счетно, но не конечно, нельзя всем элементарным исходам присвоить одинаковые вероятности. Приведём примеры того, какими могут быть вероятности на таком пространстве.
Пример 2.3. Пусть 
. Зададим вероятность элементарного исхода 
так: 
. Проверим, что набор таких вероятностей удовлетворяет определению 2.3:
(2.1)
Заметим, что (2.1) представляет собой сумму бесконечной геометрической прогрессии с первым членом 1/2 и знаменателем 1/2 < 1, тогда
.
Пример 2.4. На том же самом множестве зададим вероятности следующим образом: 
, 
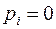для 
. Нетрудно проверить, что набор таких вероятностей удовлетворяет определению 2.3
